Задачі підвищеної складності До § 1. Лінійні рівняння з однією змінною

1122. Розв’яжіть рівняння:

а) |х  1| + |x + 1| = 0; б) |х  4| + |2x  8| = 0.

1123. Скільки коренів залежно від числа а (кажуть: параметра а) має рівняння:

 а) |х  а| = 0; б) |х| = а; в) |х  а| + |x  1| = 0?

1124. Розв’яжіть рівняння ах = а з параметром а.

● Розв’язання. Розглянемо два випадки.

1) а ≠ 0. Тоді: ах = а; х = 1 (поділили обидві частини рівняння на а).

2) а = 0. Тоді: ах = а; 0х = 0; коренем рівняння є будь-яке число.

Відповідь. Якщо а ≠ 0, то х = 1; якщо а = 0, то коренем рівняння є будь-яке число. ●

Розв’яжіть рівняння з параметром а:

1125. а) х  а = 3; б) х + а = 4; в) 3х = а;

 г) 2х = а + 2; д) 0,5х + 3а = 1,5; е) а  4х = 3а.

1126.  а) ах = 5; б) ах = 0; в) ах = 10а;

 г) (а + 2)х = 2; д) 4ах + 4а = 8а; е) а(1  х) = 5а.

1127. Дано рівняння а(х  1) + 5а = 8(х + а) + 1 з параметром а.

а) Для яких значень а рівняння не має коренів?

б) Чи існують значення а, для яких рівняння має більше, ніж один корінь?

1128. З міста А до міста В виїхав автобус і рухався зі швидкістю 60 км/год. Через півгодини він зустрів легковий автомобіль, який їхав з міста В. Цей автомобіль доїхав до міста А і через 40 хв виїхав назад до міста В. За 20 км від міста В легковий автомобіль наздогнав автобус. Знайдіть відстань між містами, якщо швидкість легкового автомобіля весь час становила 90 км/год.

1129. Сплав міді, цинку й олова, загальна маса якого дорівнює 1 кг, містить олова на 20% більше, ніж міді, а цинку  на 50% більше, ніж олова. Знайдіть масу цинку в сплаві.

1130. Оля любить каву з молоком. Коли їй дали повну чашку самої кави, вона відпила чашки і долила молоком. Потім знову відпила чашки і знову долила молоком. Після цього в чашці стало кави на 56 мл більше, ніж молока. Знайдіть місткість чашки.

1131. Велосипедист проїхав деякий шлях зі сталою швидкістю. Якби він їхав на 2 км/год швидше, то затратив би на цей шлях в 1,1 менше часу. З якою швидкістю їхав велосипедист?

До § 2. Цілі вирази

1132. Чи можна в запису _* 1 _* 2 _* 3 _* 4 _* 5 _* 6 _* 7 _* 8 _* 9 _* 10 поставити замість зірочок знаки «+» або «–» так, щоб значення одержаного числового виразу дорівнювало: а) 5;  б) 0;  в) 60?

1133. Доведіть, що для будь-якого натурального значення n значення виразу n(n + 1) + (n + 2)(n + 3) є складеним числом.

1134. Вираз а² + 2аb + 2a  b + 4 для a = 2 і деякого значення b набуває значення 0. Якого значення набуває вираз а² + аb + b² для тих самих значеннях a і b? 

1135. Для деяких натуральних значень m і n число 3m + 2n ділиться на 7. Доведіть, що для тих самих значень m і n на 7 ділиться й число:

  а) 10m + 9n; б) 4m + 5n; в) m + 3n.

1136. Для деяких натуральних значень m і n число 5m - n ділиться на 8. Для тих самих значень m і n на 8 ділиться і число 3m + 4n. Доведіть, що тоді й самі числа m і n діляться на 8.

1137. а) Доведіть, що коли два цілі числа при діленні на 7 дають рівні остачі, то різниця цих чисел ділиться на 7.

б) Доведіть, що серед будь-яких восьми цілих чисел завжди знайдуться два числа, різниця яких ділиться на 7.

1138. Запишіть формулу цілих чисел, які діляться на 5, а при діленні на 2, 3 і 4 дають в остачі 1.

1139. (Задача-жарт.) Жінка несла на базар 2 кошики яєць. Її ненароком штовхнув чоловік, кошики впали, а яйця розбилися. Чоловік, щоб розрахуватися, запитав, скільки було всього яєць. Жінка відповіла:

 Я їх не рахувала, але коли складала в кошики по 2, по 3, по 4, по 5, по 6, то щоразу залишалося по одному яйцю, а коли складала по 7, то залишилось 2 яйця. Ще знаю, що в кожний кошик поміщається не більше 70 яєць.

Скільки яєць було в кошиках?

1140. До деякого трицифрового числа праворуч дописали одну цифру і від одержаного числа відняли початкове. Виявилося, що різниця ділиться на 9. Яку цифру дописали?

1141. Доведіть, що число 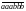ділиться на 37.

1142. а) Доведіть, що сума чисел , і кратна 111.

б) Доведіть, що не існує трицифрового числа , для якого число  +   +  було б квадратом натурального числа.

1143. Два учні по черзі пишуть n-цифрове число: число одиниць пише перший, число десятків — другий, число сотень — знову перший і т. д. Чи може другий учень досягти того, щоб одержане число ділилося на 9, якщо перший заважає йому це зробити? Розгляньте випадки: а) n = 10; б) n = 15.