
- •Алгебра Підручник для 7 класу
- •Юні друзі!
- •§ 1. Рівняння
- •1. Поняття рівняння
- •Приклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •2. Розв’язування рівнянь. Властивості рівнянь
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •3. Лінійні рівняння з однією змінною
- •Підсумок
- •Д ля тих, хто хоче знати більше Рівняння з модулями
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •4. Розв’язування задач за допомогою рівнянь
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 1
- •Завдання для самоперевірки № 1
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 2. Цілі вирази
- •5. Вирази зі змінними. Цілі вирази
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •6. Тотожно рівні вирази. Тотожності
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 2
- •Завдання для самоперевірки № 2
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 3. Одночлени
- •7. Степінь з натуральним показником
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •8. Властивості степеня з натуральним показником
- •1. Множення степенів з однаковими основами.
- •2. Ділення степенів з однаковими основами.
- •3. Піднесення степеня до степеня.
- •4. Піднесення добутку до степеня.
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •9. Одночлен та його стандартний вигляд
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 3
- •Завдання для самоперевірки № 3
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 4. Многочлени
- •10. Многочлен та його стандартний вигляд
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •11. Додавання і віднімання многочленів
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •12. Множення одночлена на многочлен
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •13. Множення многочлена на многочлен
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •14. Розкладання многочленів на множники способом винесення спільного множника за дужки
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •15. Розкладання многочленів на множники способом групування
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 4
- •Завдання для самоперевірки № 4
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 5. Формули скороченого множенея
- •16. Множення різниці двох виразів на їх суму
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •17. Квадрат суми і квадрат різниці двох виразів
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •18. Розкладання на множники різниці квадратів двох виразів
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •19. Розкладання многочленів на множники з використанням формул квадрата суми і квадрата різниці
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •20. Різниця і сума кубів двох виразів
- •П риклади розв’язання вправ
- •Рівень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •21. Застосування кількох способів для розкладання многочленів на множники
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Д ля тих, хто хоче знати більше
- •22. Застосування перетворень виразів
- •1. Порівняння значень многочлена з нулем.
- •2. Знаходження найбільшого і найменшого значень виразів.
- •3. Розв’язування задач на подільність.
- •4. Знаходження значень многочлена за допомогою мікрокалькулятора.
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 5
- •Завдання для самоперевірки № 5
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 6. Функції
- •23. Функція. Способи задання функції
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •24. Графік функції. Функція як математична модель реальних процесів
- •П риклади розв’язання вправ
- •Р івень а
- •Рівень б
- •Р івень в
- •Вправи для повторення
- •25. Лінійна функція
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 6
- •Завдання для самоперевірки № 6
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •§ 7. Системи лінійних рівнянь із двома змінними
- •26. Рівняння із двома змінними
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •27. Графік лінійного рівняння із двома змінними
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •28. Системи двох лінійних рівнянь із двома змінними
- •1. Системи лінійних рівнянь із двома змінними та їх розв’язки.
- •2. Розв’язування систем лінійних рівнянь графічним способом.
- •П риклади розв’язання вправ
- •29. Розв’язування систем лінійних рівнянь способом підстановки
- •Д ля тих, хто хоче знати більше
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •30. Розв’язування систем лінійних рівнянь способом додавання
- •Д ля тих, хто хоче знати більше
- •Вправи для повторення
- •31. Розв’язування задач за допомогою систем рівнянь
- •П риклади розв’язання вправ
- •Р івень а
- •Р івень б
- •Р івень в
- •Вправи для повторення
- •Запитання і вправи для повторення § 7
- •Завдання для самоперевірки № 7
- •1 Рівень
- •2 Рівень
- •3 Рівень
- •4 Рівень
- •Задачі за курс алгебри 7 класу
- •Задачі підвищеної складності До § 1. Лінійні рівняння з однією змінною
- •До § 2. Цілі вирази
- •До § 3. Одночлени
- •До § 4. Многочлени
- •До § 5. Формули скороченого множення
- •До § 6. Функції
- •До § 7. Системи лінійних рівнянь із двома змінними
- •Логічні задачі
- •Вітчизняні математики
- •Відомості з курсу математики 5–6 класів Подільність натуральних чисел
- •Найбільший спільний дільник
- •Найменше спільне кратне
- •Десяткові дроби
- •Звичайні дроби
- •Додатні та від’ємні числа
- •Відповіді
- •Завдання для самоперевірки № 1
- •Завдання для самоперевірки № 2
- •Завдання для самоперевірки № 3
- •Завдання для самоперевірки № 4
- •Завдання для самоперевірки № 5
- •Завдання для самоперевірки № 6
- •Завдання для самоперевірки № 7
- •Задачі за курс алгебри 7 класу
- •Задачі підвищеної складності
- •Предметний покажчик
- •Розділ і. Лінійні рівняння з однією змінною
- •Розділ іі. Цілі вирази
- •Розділ ііі. Функції
- •§ 6. Функції
- •Розділ іv. Системи лінійних рівнянь із двома змінними
- •§ 7. Системи лінійних рівнянь із двома змінними
- •Навчальне видання
- •Алгебра
- •46010, М. Тернопіль, вул. Поліська, 6а. Тел. 8-(0352)-43-10-31, 43-15-15, 43-10-21.
Завдання для самоперевірки № 7
1 Рівень
1. Вкажіть розв’язки рівняння х у = 2:
а) (3; 2); б) (3; 1); в) (5; 2); г) (3; 2).
2. Яка з пар чисел є розв’язком
системи рівнянь

а) (3; 3); б) (2; 2); в) (2; 1); г) (1; 5).
3. Розв’яжіть систему рівнянь
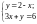 способом підстановки та вкажіть
правильну відповідь:
способом підстановки та вкажіть
правильну відповідь:
а) (1; 1); б) (0; 2); в) (2; 0); г) (4; 2).
4. Розв’яжіть систему рівнянь
 способом додавання та вкажіть правильну
відповідь:
способом додавання та вкажіть правильну
відповідь:
а) (2; 8); б) (4; 10); в) (4; 2); г) (2; 4).
5. Сума двох чисел дорівнює 21, до того ж, одне з них на 5 більше від іншого. Знайдіть ці числа.
Нехай більше число дорівнює х, а менше у. Яка система рівнянь відповідає умові задачі?
а)
 б)
б)
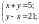 в)
в)
 г)
г)

2 Рівень
1. Доберіть замість зірочок такі числа, щоб пари (3; * ) і ( * ; 2) були розв’язками рівняння 5х 2у = 9.
2. Розв’яжіть графічно систему
рівнянь
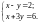
3. Розв’яжіть систему рівнянь
 способом підстановки.
способом підстановки.
4. Розв’яжіть систему рівнянь
 способом додавання.
способом додавання.
5. У магазині борошно продають у малій та великій упаковках. Загальна маса малої та великої упаковок борошна дорівнює 7 кг, а 2 малі й 3 великі упаковки мають загальну масу 19 кг. Яка маса малої упаковки борошна і яка великої?
3 Рівень
1. Знайдіть таке число а, щоб графік рівняння 2х ау = 2 проходив через точку (1; 2).
2. Розв’яжіть графічно систему
рівнянь

3. Розв’яжіть систему рівнянь
 способом додавання.
способом додавання.
4. Розв’яжіть систему рівнянь
5. За цукерки і печиво мама заплатила 15 грн. Відомо, що 25% вартості цукерок менші, ніж третина вартості печива, на 1 грн. 50 к. Скільки гривень мама заплатила за цукерки і скільки за печиво?
4 Рівень
1. Знайдіть такі числа а і b, щоб графік рівняння 2ах (b + 2)у = 2 проходив через точки (1; 4) і (2; 2).
2. Розв’яжіть графічно систему
рівнянь

3. Розв’яжіть систему рівнянь

4. Для якого
значення коефіцієнта а
система рівнянь
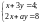 має безліч розв’язків?
має безліч розв’язків?
5. Є сталь двох сортів із вмістом нікелю 5% і 40%. Скільки сталі кожного сорту потрібно взяти, щоб після переплавки одержати 70 т сталі, яка містила б 30% нікелю?
Задачі за курс алгебри 7 класу
1047. Купили 2 кг огірків по а грн. за кілограм і 5 кг помідорів по b грн. за кілограм. Запишіть у вигляді виразу вартість покупки.
1048. Автомобіль протягом t год рухався зі швидкістю 80 км/год і протягом 2 год — зі швидкістю 70 км/год. Запишіть у вигляді виразу шлях, який проїхав автомобіль за весь час руху. Знайдіть значення цього виразу, якщо t = 1,2.
1049. Через першу трубу до басейну щохвилини поступає а л води, а через другу — b л. Скільки літрів води поступить до басейну через обидві труби за 3 год?
1050. Знайдіть значення степеня:
а) 94; б) (3)5; в) (2,5)3; г)
1051. Подайте у вигляді степеня з основою а:
a) а2а4; б) а7 : а; в) (а3)5; г) (а5 а)4.
1052. Обчисліть:
а) 0,45 2,55;
б) (22 0,52)7 0,254 44; в)
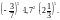
1053. Подайте одночлен у стандартному вигляді та вкажіть його степінь:
a) 8х2ху; б) 3а2b 2(а5)2; в) m3 3m2n 5n4;
г) 0,5ас (4а3с)2
а2с;
д)  е)
е) 
1054. Подайте одночлен 12a4b5 у вигляді добутку двох одночленів стандартного вигляду, одним з яких є: 2a2b2; 4a3b; 0,5b.
1055. Подайте одночлен 9a6b2 у вигляді квадрата одночлена.
1056. Подайте одночлен 27х6у9 у вигляді куба одночлена.
1057. Знайдіть значення одночлена:
а) 4а3b,
якщо а = 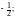 b =
b =  б) (2х3у)2 у4,
якщо х = 0,25; у = 4.
б) (2х3у)2 у4,
якщо х = 0,25; у = 4.
1058*. Спростіть вираз, де n — натуральне число:
а) (х3)3n (х5хn + 1)2; б) (аn)17 (a2)9.
1059. Запишіть многочлен у стандартному вигляді та знайдіть його степінь:
а) 3x2 - 6х + х2 - 3 + x; б) 3а × 2ab + a5 a3 - 7a2b ;
в) 0,6a2b - 1,4b2a + 2,8а2b + 3,3аb2;
г) 5x3 +  x2 -
x2 -  x3 -
x3 -  x2.
x2.
1060. Спростіть вираз:
а) 8а2 + 4а 3 (7 8а + 3а2); б) х 3х2у ху + (х2 3х2у + ху);
в) 
Виконайте множення:
1061. а) 4а(а2 4а + 3); б) (2х2 4х + 8)(0,5х2);
в) (4ab2 + 9а2)(2b2 3a); г) (a 7)(b + 1)(c 2).
1062. а) (b + 2c)(b - 2c); б) (5x - 2y)(5x + 2y);
в) (1,4a - 0,3b)(0,3b + 1,4a); г)

1063. Піднесіть до квадрата:
а) (2х + 3)2; б) (3с - 1)2; в) (0,4b - 5а)2; г)
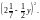
Спростіть вираз:
1064. а) (х 3)(х2 + х + 3) х3; б) 3с (с 2)(2с2 с + 1) 5с2;
в) (5 + х)(5 - х) + х2; г) (2b - 9)(2b + 9) - 4b2;
д) (n - 1)(n2 + n + 1) - n3; е) (а + 3)(а2 - 3а + 9) - 27.
1065. а) (10 3m)(2 + 3m) + (5m 4)(5 - 2m);
б) (4a + 9)(a2 2a + 2) (4a 7)(а + 1)2;
в) (n2 - 3n)(1 + 3n)(-1 + n) - 3n(n3 + 1);
г) (4y 5y2)2 + (2y + 5y2)2 20y2.
Запишіть у вигляді многочлена стандартного вигляду:
1066. а) (b + 2)(b 2)(b2 + 4); б) 15х3(х2 + 10)(10 х2);
в) а5(а4 (2а3 + а2(а2 2а + 3))) + 4а7.
1067*. а) (а2 + 2а - 2)2; б) (5x - 2)3; в) (с - 3)4.
1068. Доведіть тотожність:
а) у(b - x) + x(b + y) = b(x + y); б) (-m + n)(m - n) = -(n - m)2;
в) (a + b + c + d)2 – (a + b)2 (c + d)2 = 2(a + b)(c + d);
г) (n + 1)(n + 3)(n + 5)(n + 7) + 7 = (n2 + 8n + 8)(n2 + 8n + 14).
Розкладіть на множники:
1069. а) 2x + 2ху; б) а2 2а; в) 12xу3 + 8ху2 16х2у.
1070. а) ах ay + 3x 3y; б) x2у – 2х + xy 2;
в) 9уа 6yа2 + 2axy 3xy; г) 8x2a – 15y3 10x2y + 12ay2.
1071. а) 9n2 4m2; б) 120 – 30a4; в) 27х3 + 0,008у3;
г) х3 (m - n)3; д) a2 + 8а + 16; е) 6х2 24ху + 24у2.
1072. a)
 б)
а2 - 4b2 + 2b + a; в) х2 - 4ху + 4у2 4у4.
б)
а2 - 4b2 + 2b + a; в) х2 - 4ху + 4у2 4у4.
1073*. а) x2 2x – 3; б) а2 + 3а – 4; в) х2 8ху + 7у2.
1074. Доведіть, що значення виразу:
а) 97 312 ділиться на 8; б) 498 + 3 715 ділиться на 10.
1075. Обчисліть:
а) 97 103; б) 1,8 2,2; в) 522 – 482; г) 7,352 – 6,352.
1076. Знайдіть значення виразу:
а) а3 0,5а2, якщо а = 1,5;
б) х2 – 2xy + y2, якщо x = 0,3; y = 10,3.
1077. Доведіть, що значення виразу (х + 1)2 - (х - 1)(х + 3) не залежать від значень х.
1078. Доведіть, що для будь-якого цілого значення n значення виразу:
а) (2n + 3)2 - (2n - 1)2 ділиться на 8;
б) (8n 4)2 - 8(4n 3) не ділиться на 32.
1079. Для якого значення х значення виразу х2 + 2х + 9 є найменшим?
1080. Для якого значення х значення виразу 2 х2 + 4х є найбільшим?
1081*. Доведіть, що сума кубів двох послідовних цілих чисел, які не діляться на 3, кратна 9.
1082*. Чи може різниця четвертих степенів двох натуральних чисел бути простим числом?
1083*. Знайдіть найменше значення виразу х2 + у2 4у 2x.
1084*. Доведіть, що коли деякі два цілі числа не діляться на 3, то їх сума або різниця діляться на 3.
1085*. Два велосипедисти проїхали шлях від пункту А до пункту В. Перший велосипедист першу половину шляху їхав зі швидкістю 20 км/год, а другу половину зі швидкістю 16 км/год. Другий же велосипедист першу половину шляху їхав зі швидкістю 19 км/год, а другу половину зі швидкістю 17 км/год. Хто з них затратив більше часу на шлях від А до В?
Розв’яжіть рівняння:
1086. а) 3х 18 = 57 2х; б) 3(x – 2) – 4(х 4) = 5;
в) 250(х + 8) = 125х – 500; г) 0,3(1 – x) = 0,4(х 1) – 0,7;
д)
 е)
е)
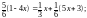
є)
 ж)
ж)

1087. а) х(х + 5) – х2 = 2; б) (2х + 3)(х – 1) = 2х2;
в) х(х + 0,1) = (х – 0,1)(х + 0,2); г) 
д) (х – 3)(х + 3) = (х + 1)2; е) 2х(х – 1,5)2 = 2х3 – 6х2 + 3.
1088. a) у3 3у2 = 0; б) х3 х = 0;
в) х2 – 6х + 9 = 0; г) х3 – 2х2 – 4х + 8 = 0;
д) у2 + 2у – 48 = 0; е) 
1089*. а) |3 2x| = 5; б) ||х| 2| = 6.
1090*. а) (|х| + 5)(3|х| 9) = 0; б) |x(х 2)| + х2 = 0; в) х2 + 2|х| + 1 = 0.
1091*. Доведіть, що рівняння x4 + 1 + (x - 2)4 = 2х2 не має коренів.
1092*. Розв’яжіть рівняння
 .
.
Розв’яжіть задачі 1093–1098, склавши рівняння.
1093. Периметр прямокутника дорівнює 68,4 см. Знайдіть сторони прямокутника, якщо одна з них на 3,6 см коротша від іншої.
1094. Сума двох чисел дорівнює 52,7, одне з них у 2,4 разу більше від другого. Знайдіть більше із цих чисел.
1095. У першій цистерні втричі більше бензину, ніж у другій. Коли з першої цистерни забрали 400 л бензину, а з другої — 800 л, виявилося, що в перший цистерні бензину стало у 8 разів більше, ніж у другій. Скільки бензину було в кожній цистерні спочатку?
1096. З міста виїхав мотоцикліст і рухався зі швидкістю 40 км/год. Через півгодини услід за ним виїхав автомобіль, швидкість якого дорівнює 60 км/год. Через скільки годин після свого виїзду з міста автомобіль наздожене мотоцикліста?
1097. Нержавіюча сталь є сплавом заліза, хрому й нікелю. Лист з такої сталі містить 15% хрому, 0,5% нікелю, а заліза — на 2,78 кг більше, ніж хрому. Знайдіть масу листа.
1098*. Автобус рухався до міста N зі швидкістю 60 км/год. Дорогою його обігнав легковий автомобіль, що їхав зі швидкістю 80 км/год. Автомобіль прибув до міста N і через 15 хв вирушив у зворотний шлях. На відстані 10 км від міста N він знову зустрів автобус. На якій відстані від міста N були автобус і автомобіль при першій зустрічі?
1099. Функція задана формулою у –2х + 3.
а) Знайдіть значення функції, які відповідають таким значенням аргументу: –2; 0; 6.
б) Знайдіть значення аргументу, якому відповідає значення функції: 3; 1.
в) Для якого значення х значення функції дорівнює значенню аргументу?
1100. Побудуйте графік функції у 2х – 0,5. За допомогою графіка знайдіть: а) значення функції, якщо х –0,5; х 1,5; б) значення х, для якого у 1,5.
1101. Побудуйте графік функції у 0,5х + 1, де 4 x 3. Яка область визначення та область значень функції? Чому дорівнюють найбільше та найменше значення функції? Вкажіть нулі функції. Для яких значень х функція набуває додатних значень; від’ємних значень?
1102. Побудуйте графік функції:
а) у –х + 1, де 3 x 2; б) y 2х2 – 2, де 2 x 2.
в) у 1,5х; г) у –1,5х; д) у 3х + 1; е) у –1,5х – 1.
1103. Графік прямої пропорційності проходить через точку A(2; 7). Чи проходить цей графік через точку B(4; 14)?
1104. На рисунку 47 зображено графік функції. Знайдіть область визначення та область значень цієї функції. Задайте функцію формулою, якщо:
а) 0 х 2; б) 2 х 6.
 Рис.
47
Рис.
47
1105. Знайдіть координати точок перетину графіків функцій:
а) у 1,5х і у –х + 5; б) у –2х і y х2.
1106. Для якого значення b графіки функцій у 3х + b і у 2х + 4 перетинаються в точці, що лежить на осі абсцис?
1107. Чи є пара чисел (2; –1) розв’язком рівняння 2х + 5у = 3?
1108. Побудуйте графік рівняння:
а) х + 3у = 3; б) 2х 3у = 6; в) 2х = 5; г) 3у = 6.
1109. Розв’яжіть графічно систему
рівнянь

Розв’яжіть систему рівнянь:
1110. а)
 б)
б)
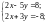 в)
в)
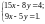
1111. а)
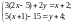 б)
б)

1112. а)
 б)
б)

1113. Знайдіть точку перетину графіків рівнянь 2х + 3у = 2 і 4х 5у = 7.
1114. Чи належить точка перетину графіків рівнянь 2х + 4у = 6 і 10х у = 12 графіку рівняння 3х + у = 1?
1115. Графік лінійної функції проходить через точки A(1; 1) і B(3; 7). Задайте цю функцію формулою.
1116*. Для якого значення k система
рівнянь
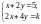 має безліч розв’язків?
має безліч розв’язків?
Розв’яжіть задачі 1117–1121, склавши систему рівнянь.
1117. Сума двох чисел дорівнює 20,5, одне з них на 2,3 більше від іншого. Знайдіть ці числа.
1118. Два автоматичні станки за 8 год спільної роботи виготовляють 2000 деталей. Перший станок за 2 год і другий за 3 год разом виготовляють 630 деталей. Скільки деталей виготовляє за годину кожний станок?
1119. З пунктів А і В, відстань між якими дорівнює 17 км, вийшли назустріч один одному два туристи і зустрілися через 2 год. Знайдіть швидкості туристів, якщо швидкість одного з них на 0,5 км/год менша від швидкості іншого.
1120. Братові й сестрі разом 10 років. Скільки років кожному з них, якщо через рік брат буде вдвічі старший від сестри?
1121*. Молоко однієї корови містить 5% жиру, а іншої — 3,5%. Змішавши молоко обох корів, одержали 10 л молока, жирність якого дорівнює 4%. Скільки для цього використали літрів молока від кожної корови?
