Д ля тих, хто хоче знати більше
22. Застосування перетворень виразів
Нам уже траплялося чимало завдань, для розв’язання яких треба було перетворювати той чи інший вираз. Здебільшого ми використовували перетворення виразів, коли розв’язували рівняння, доводили тотожності, знаходили значення виразів. Розглянемо ще деякі задачі, пов’язані з перетвореннями виразів.
1. Порівняння значень многочлена з нулем.
Приклад 1. Довести, що многочлен х2 - 8х + 18 набуває лише додатних значень.
● Виділивши із тричлена х2 - 8х + 18 квадрат двочлена, матимемо:
х2 - 8х + 18 = х2 - 8х + 16 – 16 + 18 = (х - 4)2 + 2.
Ми подали многочлен у вигляді суми двох доданків (х - 4)2 і 2. Доданок (х - 4)2 для будь-яких х набуває лише невід’ємних значень, доданок 2 — додатний. Тому вираз (х - 4)2 + 2 набуває лише додатних значень. Оскільки х2 - 8х + 18 = (х - 4)2 + 2, то й вираз х2 - 8х + 18 набуває лише додатних значень. ●
2. Знаходження найбільшого і найменшого значень виразів.
Виходячи з рівності х2 - 8х + 18 = (х - 4)2 + 2, одержаній у прикладі 1, можна вказати найменше значення многочлена х2 - 8х + 18. Воно дорівнює 2, до того ж, цього найменшого значення многочлен набуває, якщо х = 4.
Приклад 2. Знайти найбільше значення многочлена -х2 + 4х + 1.
● Спочатку даний вираз запишемо так:
-х2 + 4х + 1 = -(х2 - 4х - 1).
Тоді:
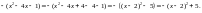
Найбільше значення многочлена дорівнює 5. ●
3. Розв’язування задач на подільність.
Приклад 3. Довести, що для будь-якого цілого значення n значення виразу (2n + 3)2 - – (2n - 3)(2n + 5) ділиться на 8.
● Спростимо даний вираз:
(2n + 3)2 - (2n - 3)(2n + 5) = 4n2 + 12n + 9 - (4n2 + 10n - 6n - 15) =
= 4n2 + 12n + 9 - 4n2 - 4n + 15 = 8n + 24 = 8(n + 3).
Для будь-якого цілого значення n добуток 8(n + 3) ділиться на 8, а тому й значення виразу (2n + 3)2 - (2n - 3)(2n + 5) ділиться на 8. ●
4. Знаходження значень многочлена за допомогою мікрокалькулятора.
Приклад 4. За допомогою мікрокалькулятора знайти значення многочлена 12х3 - 24х2 + 15х - 8, якщо х = 2,8.
● Значення даного многочлена шукати зручніше, якщо його попередньо перетворити так:
12х3 - 24х2 + 15х - 8 = (12х2 - 24х + 15)х - 8 = ((12х - 24)х + 15)х - 8.
Якщо х = 2,8, то схема обчислень є такою:
12 |
|
2,8 |
- |
24 |
|
2,8 |
+ |
15 |
|
2,8 |
- |
8 |
= |
Виконавши обчислення, знайдемо значення многочлена. Воно дорівнює 109,264. ●
Усно
715. Знайдіть найменше значення виразу:
а) x2 + 7; б) (а 6)2; в) (b 1)2 + 3.
716. Знайдіть найбільше значення виразу:
a) 7 - х2; б) 1 (х 2)2; в) 5 (x + 5)2.
За якого значення х вираз набуває найбільшого значення?
Р івень а
Доведіть, що вираз набуває лише невід’ємних значень:
717. а) x2 + 2x + 1; б) 4m2 + 4mn + n2 + 3.
718. а) a2 4а + 4; б) x2 2xy + y2 + 4.
Доведіть, що значення виразу ділиться на дане число:
719. а) 2452 2362 на 9; б) 4382 622 на 500;
в) 523 363 на 16; г) 753 + 253 на 100.
720. а) 8112 7122 на 99; б) 483 193 на 29.
За допомогою мікрокалькулятора знайдіть значення многочлена:
721. а) 4х3 - 6х2 + 5х - 3, якщо х = 5; х = 3,2; х = 2,6;
б) 1,2х3 + 2,4х2 + 0,5х - 1, якщо х = 1,7;
в) 4,5х4 + 4х3 3,5х2 + 2х - 1,8, якщо х = 4.
722. а) 15х3 - 8х2 + 12х - 30, якщо х = 2; х = 1,2; х = 4;
б) 2,4х4 - 7,2х3 3,3х2 + 4,5х, якщо х = 3.