Р івень в
508. Розкладіть на множники: a3 - a2 + b3 - b2 + a2b + b2a.
509. Дано многочлен x3 - х2 + 3x 3. Доведіть, що для x > 1 він набуває лише додатних значень.
510. Для яких значень х значення многочленна 3x3 - 9х2 + 4x 12 додатні; від’ємні?
511. Розв’яжіть рівняння: (x2 - х)(6 + 5x + x2) = x3(х + 4) - 5.
512. Розкладіть на множники тричлен:
а) a2 - 7a + 10; б) x2 + 5x + 4;
в) x2 + 3xy + 2y2; г) а2 - 7аb + 12b2.
Розв’яжіть рівняння:
513. а) x2 - 3x + 2 = 0; б) х2 + 8х + 15 = 0.
514. а) (x 2)2 + 6(x 2) + 8 = 0; б) (x2 5x)2 + 10(x2 5x) + 24 = 0.
Вправи для повторення
515. Обчисліть:
а) 33 93 273; б) 45 0,255 + 23 43 0,253;
в) 25(26 1) 23(28 22); г) 33(33 4) 32(34 + 4).
516. За 3 товстих i 5 тонких зошитів Олег заплатив 5 грн. 60 коп. Товстий зошит дорожчий від тонкого на 80 коп. Скільки коштує товстий зошит?
517. На двох полицях було 95 книжок. Коли четверту частину книжок, що стояли на першій полиці, переставили на другу, то на другій полиці книжок стало на 5 більше, ніж на першій. Скільки книжок було на кожній полиці спочатку?
518. Площа першої ділянки дорівнює
63 га, а другої — 53 га. З першої
ділянки господарство зібрало картоплі
в
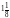разу більше, ніж із другої. Яка врожайність
картоплі на кожній ділянці, якщо
врожайність на першій ділянці на 1,5 т
менша, ніж на другій?
519. Прочитайте вираз словами:
а) a + b; б) а b; в) а2 b2; г) (a – b)(а + b).
Запитання і вправи для повторення § 4
1. Дайте означення многочлена. Наведіть приклади многочленів.
2. Який многочлен називають многочленом стандартного вигляду?
3. Що називають степенем многочлена? Наведіть приклад многочлена другого степеня.
4. Знайдіть суму та різницю многочленів 2х + 4 і х + 2.
5. Як помножити одночлен на многочлен?
6. Як помножити многочлен на многочлен?
7. Що означає розкласти многочлен на множники?
8. Як розкладають многочлен на множники способом винесення спільного множника за дужки? Поясніть це на прикладі многочлена 2a2 + 4ab.
9. На прикладі многочлена 2a – 2b + na – nb поясніть, як розкладають многочлен на множники способом групування.
520. Запишіть многочлен у стандартному вигляді та знайдіть його степінь:
a) 4a2 3a + 1 + а2 5a + 7; б) 2х3 + 2 2х3 + 5х 3 + 3х2;
в) 3aba 2a2b + b2a2 + ab 4a; г) x2y - хy2 + 2x - 6хy (- x) - 3x.
521. Знайдіть суму многочленів:
a) 2a + 3 і 5a 2; б) 5x3 3x2 + 2x і x3 + 3x2 2;
в) 2x2 3xy + y2 і x2 + 2xy y2; г) х2 2х + 3; 2х2 5 і -2x + 2.
522. Знайдіть різницю многочленів:
а) 3с2 4с + 1 і 3с2 + с - 5;
б) 3х3 - 4х2 + 3х - 4 і -3х3 - 4х2 + 11;
в) 2а5 - 8а4 + а2 + 5 і -8а4 + а3 - 2а - 5;
г) аb + 3а2b + 3 і 2аb - 5 + 3а2b.
Виконайте множення і результат запишіть у вигляді многочлена стандартного вигляду:
523. a) a(4a 3); б) 2b(b2 + 5b 2);
в) (x2 + 3x + 2) 2x; г) (3c2 + 3c 2) (-2с2);
д) (a 2)(3a 4); е) (n - 2m)(n + 2m);
є) (a 6)(2a2 а + 3); ж) (2c - d + 3)(3c + 2d).
524. а) (х2 - 2х + 1)(х2 + х - 4); б) (х + 2)(3х - 1)(2х + 7);
в) (т - 4n)(4m2 + mn - n2); г) (-ab2 + 4a3)(4a2b + b3).
525. Спростіть вираз:
а) (4 3b)(b - 3) + (5b 4)(3b - 3);
б) (8 2х)(2 + х) + (х 2)(4 + 2х);
в) ab(2a - b - 1) - (2a - 1)(ab - 1);
г) (n + 2)(n2 - 2n 3) (n 3)(n2 + 3n + 2);
д) (a + b c)(a b + c) (a b c)(a + b + c);
е) x6(x7 (x8 + x7(x2 x + 1))) + x15.
526. Доведіть тотожність:
а) (а + 1)(а2 - 4) = (а2 - а - 2)(а + 2);
б) x2 + (a + b)x + ab = (x + a)(x + b);
в) b8 + b4 + 1 = (b4 b2 + 1)(b4 + b2 + 1);
г) a4 + a2b2 + b4 = (a2 ab + b2)(a2 + ab + b2).
527. Розв’яжіть рівняння:
а) 4х(2х + 1) - 8х2 = -4; б) (х + 3)(х 1) + 6 = х2;
в)
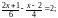г)
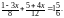
528. Доведіть, що для кожного цілого значення n значення виразу (3n + 1)(2n 1) + n + 7 ділиться на 6.
529. Доведіть, що значення виразу (5х + 1)(5х + 3) 5х(5х + 4) не залежать від значень х.
530. Периметр прямокутника дорівнює 24 см. Якщо його довжину збільшити на 3 см, а ширину зменшити на 2 см, то площа зменшиться на 5 см2. Знайдіть довжину і ширину прямокутника.
531*. Розв’яжіть рівняння:
а) (x 1)(x 3) + х(x + 1)(x4 + 1) = x6 + x5;
б) (2|x| 3)(3|x| + 2) = (2|x| + 1)(3|x| 2);
в) (xn + x)(xn + 1) xn(xn + x + 1) = 2x + 1, де n натуральне число.
Розкладіть на множники:
532. а) 2ах - 2ау; б) 8c4 - 12c2;
в) х4 + 2х3 3х2; г) 8а3 12a2 + 8а;
д) -0,6а3b4 + 0,4а2b3; е)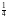 
ху - 
xz + 2x2.
533. a) 2a + 2b + xa + хb; б) 3x 3y ax + ay;
в) х3 + 2х2 + х + 2; г) 0,1x 0,2xy + 0,2y 0,4у2;
д) 5а2b + 10а2 20bc 10b2c; е) 4x2z + 25y3 5x2y 20y2z.
534*. а) х2 - 9х + 14; б) х2 + 8х + 12.
Розв’яжіть рівняння:
535. a) у2 3у = 0; б) х2 + 2х = 0.
в) 0,8x2 + 2x = 0; г)
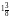x2 = 
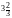x.
536*. а) х2 5х + 6 = 0; б) у2 + 4у + 3 = 0.
537. Знайдіть значення виразу:
а) bc + c2 5b 5c, якщо b = 3,6; c = 1,4;
б) m2 mn 4m + 4n, якщо m = 12,5; n = 2,5;
в) 4ay 4ax 2x + 2y, якщо a = 2; x = 0,01; y = 6,99.
538. Доведіть, що значення виразу:
а) 314 – 312 ділиться на 8; б) 498 + 3 · 715 ділиться на 10.
539*. Доведіть, що значення виразу 242 + 420 + 815 - 1612 ділиться на 219.
540*. Сума чисел x та y дорівнює 1. Доведіть, що для цих чисел правильною є рівність x2 + xy – 2x – y + 1 = 0.
541*. Розв’яжіть рівняння 2x3 – x2 + 8x – 4 = 0.