Питання для самоконтролю

1. Скільки ступенів вільності має тверде тіло, що обертається навколо нерухомої точки?

2. Чому обертання твердого тіла навколо нерухомої точки називають сферичним рухом?

3. Запишіть рівняння обертання твердого тіла навколо нерухомої точки.

4. Що називається кутовою швидкістю твердого тіла, яке обертається навколо нерухомої точки?

5. Сформулюйте теорему Ейлера-Даламбера.

6. Як зображується вектор кутової швидкості твердого тіла, що обертається навколо нерухомої точки?

7. Запишіть формули, за допомогою яких можна визначити вектор кутового пришвидшення тіла, що обертається навколо нерухомої точки.

8. Чому в кожний момент часу вектор швидкості точки тіла, котре здійснює сферичний рух, можна визначити за формулою Ейлера?

9. Запишіть формулу Ейлера, яка визначає вектор швидкості точки тіла в обертальному русі.

10. За якою формулою визначається величина швидкості точки тіла, котре здійснює сферичний рух?

11. Запишіть формули, які визначають проекції на нерухомі осі координат вектора швидкості точки тіла, яке здійснює сферичний рух.

12. Сформулюйте теорему Рівальса.

13. За якою формулою визначається величина доосьового пришвидшення?

14. За якою формулою визначається величина обертального пришвидшення точки тіла в сферичному русі?

15. Тіло обертається навколо нерухомої точки. В даний момент часу проекції вектора кутової швидкості на нерухомі осі координат мають значення: с^–1, , . Що в даний момент часу є миттєвою віссю обертання тіла?

16. В деякий момент часу тіло, яке обертається навколо нерухомої точки, має кутову швидкість 2 с^–1, кутове пришвид-шення 3 с^–2. Вектор кутової швидкості в даний момент часу напрямлений вздовж осі абсцис, а вектор кутового пришвидшення – вздовж осі ординат. Знайти величину швидкості точки М (0,4; 0,3; 0). Координати точок задані в метрах. Початок системи координат знаходиться в нерухомій точці тіла.

17. За умовою питання №16 визначити доосьове пришвидшення точки М.

18. За умовою питання №16 знайти величину обертального пришвидшення точки М.

19. За умовою питання №16 вказати напрям вектора швидкості точки М.

20. За умовою питання №16 вказати напрям вектора доосьового пришвидшення точки М.

21. За умовою питання №16 вказати напрям вектора обертального пришвидшення точки М.

§ 48 Рух вільного твердого тіла

Розглянемо рух вільного твердого тіла, тобто тіла, рух якого не обмежений в’язями. Для визначення його положення в просторі введемо такі системи координат (рис. 144): – нерухому систему координат; – рухому систему координат, яка рухається поступально відносно осей і з’єд-нана з тілом тільки однією точкою – точкою ; – рухому систему координат, яка жорстко з’єднана з твердим тілом. В рухомій системі координат тіло має одну закріплену (нерухому) точку – точку , отже, тіло в даній системі координат здійснює рух, розглянутий в попередньому параграфі, згідно з яким положення тіла в даній системі координат можна визначити кутами Ейлера . Для визначення положення тіла відносно нерухомої системи координат треба, крім цього, задати положення точки , а для цього потрібні ще три величини: – координати точки в нерухомій системі координат. Таким чином, положення вільного твердого тіла визначається шістьма параметрами: . Функціональна залежність даних параметрів від часу

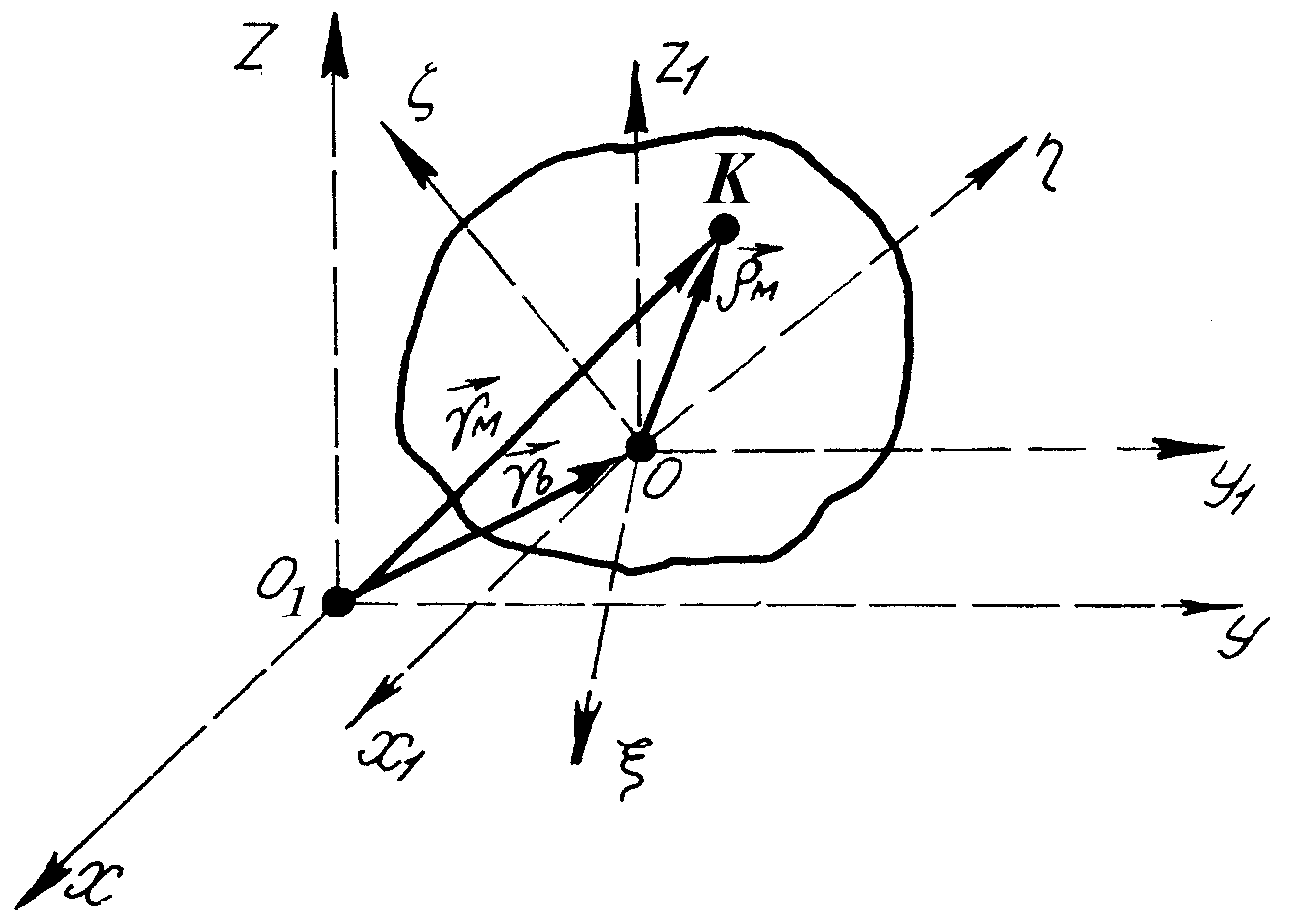
Рис. 144

;

; (2.92)

визначатиме рівняння руху вільного твердого тіла, бо за допомогою цих рівнянь можна визначити положення тіла в будь-який момент часу.

Звернемо увагу на те, що рух вільного твердого тіла є складним. Він складається з поступального руху разом з деякою точкою, яка називається, як і в плоскопаралельному русі полюсом, і обертання навколо даної точки. І дійсно, в частковому випадку, коли

;

; (2.92)

,

де – деякі константи, отримаємо поступальний рух твердого тіла. А у випадку, коли

;

;

,

тіло буде обертатись навколо нерухомої точки.

Оскільки за полюс можна взяти будь-яку точку твердого тіла, то, вибираючи різні точки тіла за полюс, отримаємо безліч розкладень руху вільного тіла на поступальну і обертальну частини. Легко довести, що поступальна частина руху залежить від вибору полюса, а обертальна – не залежить. Це саме було отримано для плоскопаралельного руху (див. § 46.2).

Для обертального руху твердого тіла навколо точки згідно з попереднім параграфом в кожний момент часу існує миттєва вісь обертання, яка проходить через точку . Отже, в кожний момент часу рух вільного тіла можна розглядати, як сукупність двох рухів: поступального разом з деякою точкою і обертального навколо деякої миттєвої осі, яка проходить через дану точку.

Перейдемо до визначення швидкостей точок вільного тіла. Швидкість довільної точки дорівнює похідній за часом від радіуса-вектора , який визначає її положення в нерухомій системі відліку. На підставі рис. 144 маємо

.

Отже,

.

Оскільки – швидкість точки , а похідна є швидкість точки відносно точки – , то отримуємо

. (2.93)

Отриману формулу можна прочитати так:

швидкість будь-якої точки вільного тіла дорівнює геометричній сумі швидкості довільно вибраного полюса і швидкості даної точки в обертальному русі тіла навколо полюса.

Продиференціювавши векторну рівність (2.93) за часом

і знаючи, що перша похідна за часом від вектора лінійної швидкості визначає вектор відповідного лінійного пришвидшення, отримаємо

, (2.94)

тобто:

пришвидшення будь-якої точки вільного тіла дорів-нює геометричній сумі пришвидшення полюса і при-швидшення даної точки в обертальному русі тіла навколо полюса.

Таким чином, отримано формули, які дають змогу обчислювати швидкість (формула 2.93) і пришвидшення (формула 2.94) будь-якої точки вільного тіла. В даних формулах вектори і визначається так, як було вказано в попередньому параграфі.