
- •Рецензенти:
- •76019, Івано-Франківськ, вул. Карпатська, 15 Івано-Франківський національний технічний університет нафти і газу
- •§ 2 Основні поняття теоретичної механіки
- •1 Статика твердого тіла
- •§ 3 Предмет статики твердого тіла
- •§ 4 Основні поняття статики
- •§ 5 В’язі та їх реакції
- •§ 6 Вихідні положення (аксіоми) статики
- •1. Аксіома зрівноваження двох сил.
- •2. Аксіома приєднання і виключення зрівноваженої системи сил.
- •3. Аксіома дії і протидії (ііі-ій закон Ньютона).
- •4. Аксіома накладання додаткових в’язей.
- •5. Аксіома паралелограма.
- •1.1 Система збіжних сил
- •§ 7 Зведення системи збіжних сил до канонічного вигляду
- •1. Геометричний спосіб визначення рівнодійної.
- •2. Аналітичний спосіб визначення рівнодійної.
- •§ 8 Умови і рівняння рівноваги системи збіжних сил
- •1. Геометрична умова рівноваги.
- •2. Аналітичні умови рівноваги. Рівняння рівноваги.
- •§ 9 Алгоритм розв’язання задач на рівновагу
- •Питання для самоконтролю
- •1.2 Теорія моменту сил
- •§ 10 Момент сили відносно точки
- •§ 11 Момент сили відносно осі
- •§ 12 Залежність між моментом сили відносно точки і моментом сили відносно осі, яка проходить через цю точку
- •§ 13 Аналітичне визначення моменту сили відносно довільної точки
- •§ 14 Теорема Варіньйона
- •Питання для самоконтролю
- •1.3 Довільна система сил
- •§ 15 Головний вектор і головний момент системи сил
- •1. Геометричний спосіб
- •2. Аналітичний спосіб
- •§ 16 Пара сил і її момент
- •§ 17 Еквівалентність пар сил
- •§ 18 Додавання пар сил
- •§ 19 Лема про паралельний перенос сили
- •§ 20 Зведення довільної системи сил до заданого центра
- •§ 21 Окремі випадки зведення довільної системи сил
- •§ 22 Інваріанти довільної системи сил
- •§ 23 Аналітичні умови рівноваги просторової системи сил
- •§ 24 Аналітичні умови рівноваги плоскої системи сил
- •§ 25 Статично означені і статично неозначені задачі
- •§ 26 Рівновага системи тіл
- •Питання для самоконтролю
- •1.4 Деякі спеціальні питання статики
- •§ 27 Тертя ковзання
- •§ 28 Конус тертя. Область рівноваги
- •§ 29 Тертя кочення
- •§ 30 Поняття про ферми
- •Питання для самоконтролю
- •1.5 Система паралельних сил. Центр ваги твердого тіла
- •§ 31 Зведення системи паралельних сил до канонічного вигляду
- •§ 32 Центр ваги твердого тіла
- •1. Центр ваги однорідного тіла (центр ваги об’єму)
- •2. Центр ваги площі однорідного плоского тіла (центр ваги площі)
- •3. Центр ваги однорідного лінійного тіла (центр ваги лінії)
- •§ 33 Центр ваги деяких простих геометричних фігур
- •§ 34 Способи визначення положення центра ваги тіла
- •Питання для самоконтролю
- •2 Кінематика
- •§ 35 Предмет кінематики
- •2.1 Кінематика точки
- •§ 36 Векторний спосіб вивчення руху точки
- •§ 37 Координатний спосіб вивчення руху точки
- •§ 38 Швидкість і пришвидшення точки в полярних координатах
- •§ 39 Натуральна система координат
- •§ 40 Натуральний спосіб вивчення руху точки
- •§ 41 Класифікація руху точки за її пришвидшеннями
- •Питання для самоконтролю
- •2.2 Кінематика твердого тіла
- •§ 42 Поступальний рух твердого тіла
- •§ 43 Обертання твердого тіла навколо нерухомої осі
- •§ 43.1 Рівняння обертання тіла навколо нерухомої осі
- •§ 43.2 Рівняння рівномірного і рівнозмінного обертання
- •§ 43.3 Швидкість і пришвидшення точки тіла, яке обертається навколо нерухомої осі
- •§ 43.4 Вектор кутової швидкості
- •§ 43.5 Векторні вирази швидкості, доцентрового і обертального пришвидшень точки тіла при обертальному русі
- •Питання для самоконтролю
- •2.1 Кінематика складного руху точки
- •§ 44 Складний рух точки
- •§ 44.1 Основні поняття і визначення
- •§ 44.2 Теорема про складання швидкостей
- •§ 44.3 Теорема про складання пришвидшень (Теорема Коріоліса)
- •§ 44.4 Коріолісове пришвидшення і його визначення
- •Питання для самоконтролю
- •2.4 Кінематика складного руху твердого тіла
- •§ 45 Складний рух твердого тіла
- •§ 46 Плоскопаралельний (плоский) рух твердого тіла
- •§ 46.1 Основні поняття і визначення
- •§ 46.2 Рівняння руху плоскої фігури
- •§ 46.3 Рівняння руху точки плоскої фігури
- •§ 46.4 Теорема про швидкості точок плоскої фігури та її наслідок
- •§ 46.5 Миттєвий центр швидкостей
- •§ 46.6 Способи визначення положення миттєвого центра швидкостей
- •§ 46.7 Теорема про пришвидшення точок плоскої фігури
- •§ 46.8 Миттєвий центр пришвидшень
- •Питання для самоконтролю
- •§ 47 Обертання твердого тіла навколо нерухомої точки
- •§ 47.1 Кути Ейлера. Рівняння обертання твердого тіла навколо нерухомої точки
- •§ 47.2 Теорема Ейлера-Даламбера
- •§ 47.3 Кутова швидкість і кутове пришвидшення тіла, що обертається навколо нерухомої точки
- •§ 47.4 Швидкість точок твердого тіла, яке обертається навколо нерухомої точки
- •§ 47.5 Пришвидшення точок твердого тіла, яке обертається навколо нерухомої точки
- •Питання для самоконтролю
- •§ 48 Рух вільного твердого тіла
- •Питання для самоконтролю
- •§ 49 Синтез рухів
- •§ 49.1 Складання поступальних рухів твердого тіла
- •§ 49.2 Складання поступального і обертального рухів твердого тіла
- •§ 49.3 Складання обертань навколо осей, що перетинаються
- •§ 49.4 Складання обертань навколо паралельних осей
- •Питання для самоконтролю
- •§ 50 Аналогії між кінематикою і статикою
- •1 Проекція вектора на площину
- •2 Проекція вектора на вісь
- •3 Приклади розв’язування задач на рівновагу тіла
- •4 Додавання двох паралельних сил
- •5 Доведення теореми про еквівалентність пар сил
- •6 Найменше значення головного моменту системи сил
- •Список використаної літератури, деяких підручників і навчальних посібників з теоретичної механіки
- •Предметний покажчик
3. Центр ваги однорідного лінійного тіла (центр ваги лінії)
Позначимо – вагу одиниці довжини однорідного лінійного тіла. Тоді його вага і вага його елементарної частини визначається за формулами
![]() (в)
(в)
де:
![]() – довжина тіла;
– довжина тіла;
![]() – довжина
-ого
елемента. Підставляючи (в) у формули
1.69), отримаємо формули, які визначають
координати центра ваги лінійного
однорідного тіла (наприклад, дроту,
стрижневої конструкції і т.ін.)
– довжина
-ого
елемента. Підставляючи (в) у формули
1.69), отримаємо формули, які визначають
координати центра ваги лінійного
однорідного тіла (наприклад, дроту,
стрижневої конструкції і т.ін.)
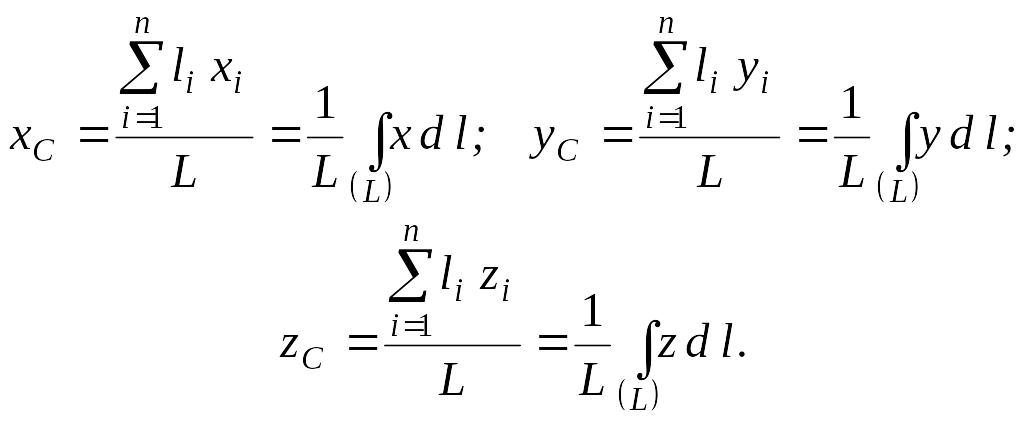 (1.75)
(1.75)
Під центром ваги лінії розуміють центр ваги тонкого однорідного тіла (стрижня), середня лінія якого співпадає з даною лінією. Координати центра ваги лінії визначаються за формулами (1.75).
§ 33 Центр ваги деяких простих геометричних фігур
Визначимо центри ваги деяких найпростіших геометричних фігур, які часто зустрічаються в практиці і за допомогою яких можна побудувати більш складні фігури.
Але з самого початку доведемо таку теорему:
якщо тіло має елемент симетрії (площину, вісь, центр симетрії), то центр ваги тіла знаходиться на цьому елементі симетрії.
Дану
теорему доведемо для тіла, що має площину
симетрії. Припустимо, що тіло А
(рис. 77) має площину симетрії
.
Систему координат виберемо так, щоб
координатна площина
знаходилась в площині симетрії. Тоді
вісь
буде перпендикулярна до цієї площини.
При такому виборі системи координат
кожній точці
![]() верхньої частини тіла, положення якої
визначається координатами (
),
буде відповідати симетрична точка
верхньої частини тіла, положення якої
визначається координатами (
),
буде відповідати симетрична точка
![]() нижньої частини тіла з координатами
(
нижньої частини тіла з координатами
(![]() ).
Якщо навколо даних точок виділити
однакові елементарні об’єми
).
Якщо навколо даних точок виділити
однакові елементарні об’єми
![]() ,
то отримаємо
,
то отримаємо
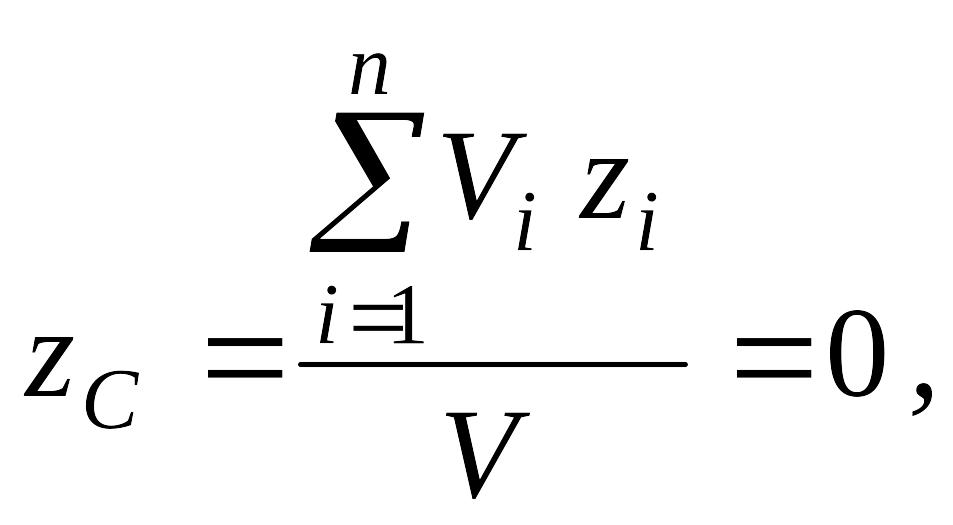 (г)
(г)
оскільки
в сумі
![]() всі члени попарно знищуються. Отриманий
результат, тобто рівність (г), вказує на
те, що центр ваги
знаходиться в площині
,
яка є площиною симетрії тіла.
всі члени попарно знищуються. Отриманий
результат, тобто рівність (г), вказує на
те, що центр ваги
знаходиться в площині
,
яка є площиною симетрії тіла.

Рис. 77
Аналогічно можна довести, що центр ваги тіла знаходиться на осі симетрії або в центрі симетрії тіла, якщо воно має відповідні елементи симетрії. Доведення цього положення може базуватись на тому, що вісь симетрії – це лінія перетину двох площин симетрії, а центр симетрії – це точка перетину трьох площин симетрії. Якщо центр ваги тіла одночасно знаходиться в двох (трьох) площинах симетрії, то, очевидно, він знаходиться на лінії (точці) перетину цих площин симетрії.
А тепер розглянемо деякі прості геометричні фігури.
Центр ваги площі паралелограма
З курсу математики середньої школи відомо, що точка перетину діагоналей паралелограма є центром його симетрії. Отже, центр ваги паралелограма (прямокутника, ромба) знаходиться в точці перетину його діагоналей.
Центр ваги площі трикутника
Д
Рис. 78
Розбиваючи трикутник на елементарні смужки лініями, що паралельні стороні АВ (рис. 78), отримаємо, що центр ваги площі трикутника буде знаходитись на медіані DM.
Отже,
центр ваги площі трикутника знаходиться в точці перетину його медіан.
В аналітичній геометрії доводиться, що координати точки перетину медіан трикутника визначаються за формулами
![]() (1.76)
(1.76)
Формули
(1.76) визначають координати центра ваги
трикутника. В цих формулах
![]() – координати вершин трикутника.
– координати вершин трикутника.
Центр ваги дуги кола
Розглянемо
дугу ADВ
кола радіуса R
з центральним кутом
![]() .
Помістимо початок системи координат в
центрі кола, а вісь Ох
проведемо як вісь симетрії дуги (рис.
79). Оскільки вісь Ох
є віссю симетрії дуги, то центр ваги її
буде знаходитись на цій осі, тобто
.
Помістимо початок системи координат в
центрі кола, а вісь Ох
проведемо як вісь симетрії дуги (рис.
79). Оскільки вісь Ох
є віссю симетрії дуги, то центр ваги її
буде знаходитись на цій осі, тобто
![]() ,
і залишається знайти тільки
,
і залишається знайти тільки
![]() .
Для цього скористаємося формулою
.
Для цього скористаємося формулою
Рис. 79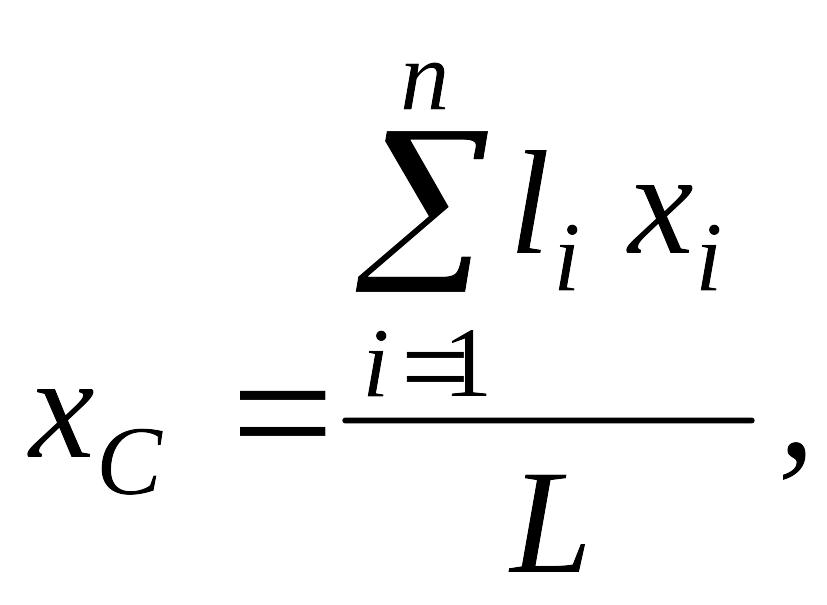
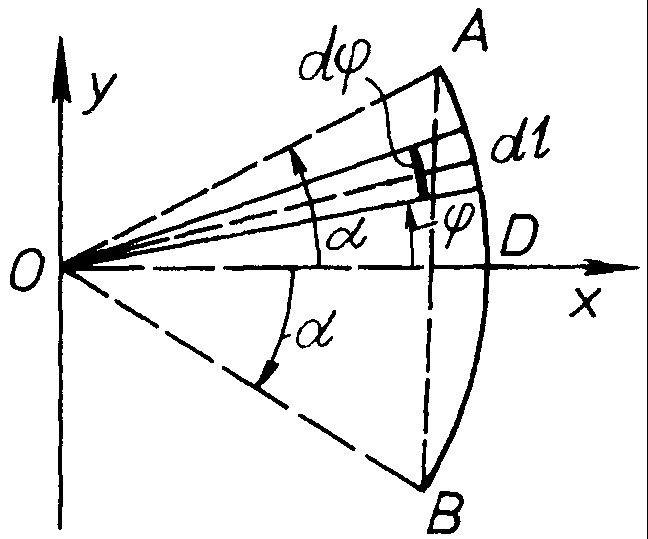
в якій сумування замінимо інтегруванням, тобто
![]() (а)
(а)
В даній формулі – довжина дуги, яка вираховується за формулою
![]() (б)
(б)
Щоб
вирахувати інтеграл, який стоїть в
чисельнику, під кутом
виділимо елемент дуги
![]() ,
центральний кут якої
,
центральний кут якої
![]() ,
тоді
,
тоді
![]() .
Координата
.
Координата
![]() виділеного елемента дуги, згідно з рис.
79 визначиться за формулою
виділеного елемента дуги, згідно з рис.
79 визначиться за формулою
![]()
Тоді
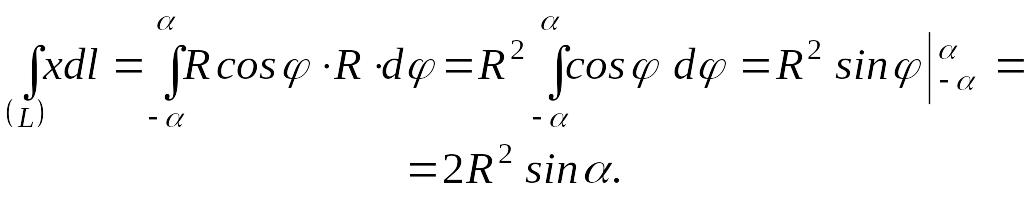 (в)
(в)
Підставляючи (б) і (в) в (а), отримаємо
![]() ,
,
або
![]() (1.77)
(1.77)
Отримана формула визначає центр ваги дуги радіуса . В даній формулі – половина центрального кута дуги в радіанах.
В
частковому випадку для дуги півкола
![]() будемо мати
будемо мати
![]() (1.78)
(1.78)
Центр ваги площі кругового сектора
Д
Рис. 80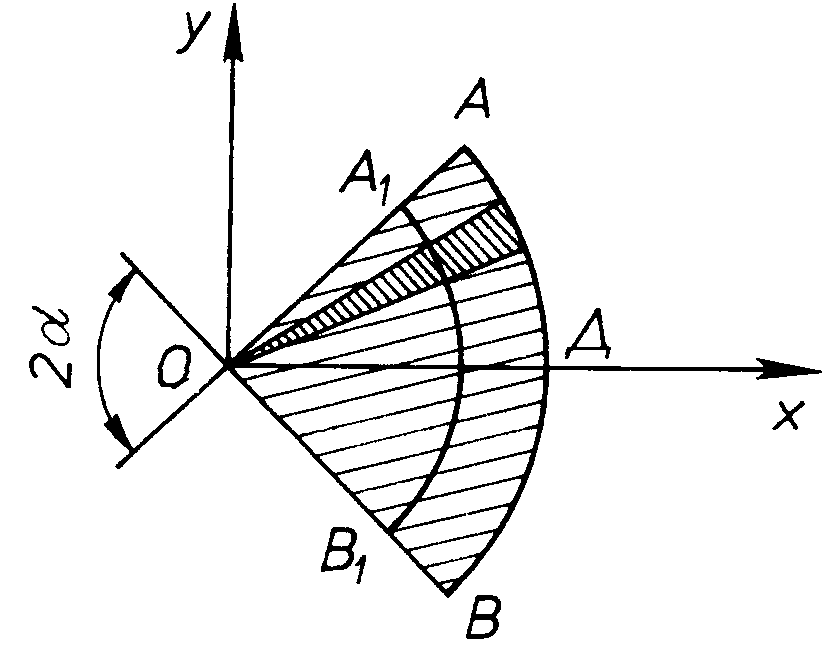
![]() від вершини. Отже, геометричним місцем
центрів ваг всіх елементарних секторів
є дуга
від вершини. Отже, геометричним місцем
центрів ваг всіх елементарних секторів
є дуга
![]() кола радіуса
кола радіуса
![]() .
Знай-шовши центр ваги цієї дуги, тим
самим знайдемо центр ваги площі кругового
сектора. Застосовуючи формулу (1.77),
отримаємо
.
Знай-шовши центр ваги цієї дуги, тим
самим знайдемо центр ваги площі кругового
сектора. Застосовуючи формулу (1.77),
отримаємо
![]() (1.79)
(1.79)
Отримана
формула визначає центр ваги площі
сектора круга радіуса
.
В цій формулі
– половина центрального кута в радіанах.
В частковому випадку, для півкруга
![]() отримаємо
отримаємо
![]() (1.80)
(1.80)
Формули для визначення положення центра ваги інших геометричних фігур можна знайти в різних технічних довідниках.
