§ 47.5 Пришвидшення точок твердого тіла, яке обертається навколо нерухомої точки

Розглянемо тверде тіло, яке обертається навколо нерухомої точки , і візьмемо в ньому яку-небудь точку (рис. 141). На цьому ж рисунку зображено:

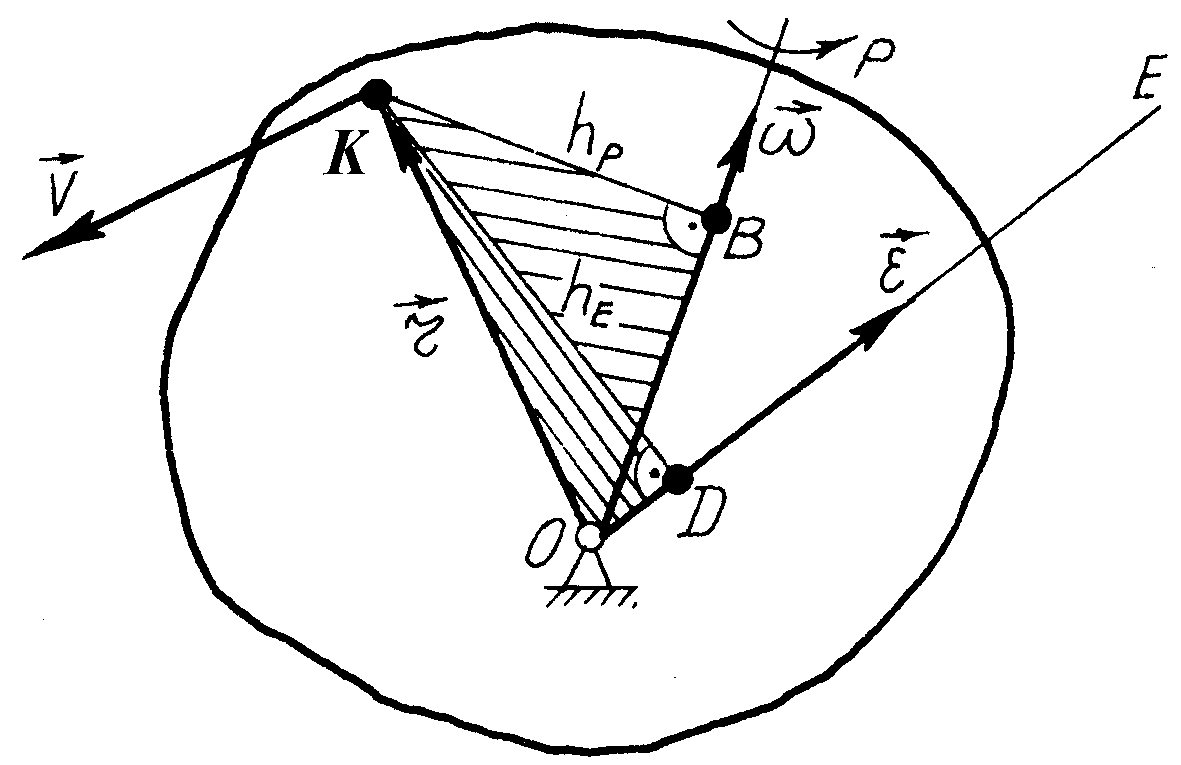
Рис. 141

– миттєву вісь обертання;

– миттєву лінію кутового пришвидшення;

– вектори відповідно кутової швидкості і кутового пришвидшення тіла в деякий момент часу;

– відстань точки до миттєвої осі обертання;

– відстань даної точки до лінії кутового пришвидшення;

– вектор швидкості точки , який згідно з попереднім визначається за формулою

.

За визначенням пришвидшення (пришвидшення – це перша похідна за часом від вектора швидкості) і, враховуючи правило диференціювання векторного добутку, матимемо

.

Враховуючи, що , а , отримаємо

. (а)

Таким чином, шукане пришвидшення складається з двох доданків. Знайдемо величину і напрями цих доданків і введемо відповідні позначення.

Векторний добуток називається обертальним пришвидшенням і позначається . Отже,

. (2.86)

Його величина, згідно з правилами обчислення векторного добутку, дорівнює

.

З (рис. 141) маємо .

Отже

. (2.87)

Обертальне пришвидшення точки тіла, яке рухається навколо нерухомої точки, чисельно дорівнює добутку кутового пришвидшення тіла на відстань даної точки до лінії кутового пришвидшення.

Вектор обертального пришвидшення за визначенням векторного добутку перпендикулярний до площини, яка проходить через вектори і , або, що те саме, – до площини, яка проходить через вектор кутового пришвидшення і точку (див. рис. 141) і напрямлений в бік, звідки поворот на кут, менший 180, першого вектора до другого – , щоб їх сумістити, видно проти руху годинникової стрілки.

Треба зазначити, що в даному випадку обертальне пришвидшення не можна називати дотичним, бо воно загалом не співпадає з напрямом вектора швидкості . І дійсно, швид-кість напрямлена перпендикулярно до площини, яка утворена векторами і , а напрямлено перпендикулярно до площини, яка утворена векторами і . Вектори і мають різні напрями, і загалом дані площини не співпадають.

Векторний добуток називається доосьовим пришвидшенням і позначається , тобто:

. (2.88)

Його величина

.

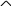Оскільки вектори і взаємно перпендикулярні (див. попередній параграф) і , отримаємо

.

Отже,

доосьове пришвидшення точки тіла, яке здійснює сферичний рух, чисельно дорівнює добутку квадрата кутової швидкості тіла на відстань даної точки до миттєвої осі обертання

. (2.89)

Щодо напряму цього пришвидшення, то воно перпендикулярне до площини побудованого на векторах і прямокутника (рис. 142), де для побудови цього прямокутника вектор умовно зображено в точці . Перпендикуляром до цієї площини є відрізок , тобто перпендикуляр, який опущений з точки на миттєву вісь обертання. Отже, вектор доосьового пришвидшення напрямлений вздовж перпендикуляра, опущеного з точки, пришвидшення якої визначається, на миттєву вісь обертання. За визначенням векторного добутку легко переконатись, що цей вектор буде напрямлений до миттєвої осі обертання. Ось чому він називається доосьовим. Враховуючи введені позначення, формула (а) набуває вигляду

Рис. 142

, (2.90)

тобто,

пришвидшення точки твердого тіла, яке обертається навколо нерухомої точки, дорівнює геометри-чній сумі її обертального і доосьового пришвидшень.

Цю тезу часто називають теоремою Рівальса.

Загалом вектори обертального і доосьового пришвидшень не перпендикулярні один до одного, а тому величину пришвидшення вираховують як діагональ паралелограма, який будується на векторах і (рис. 143) за формулою

. (2.91)

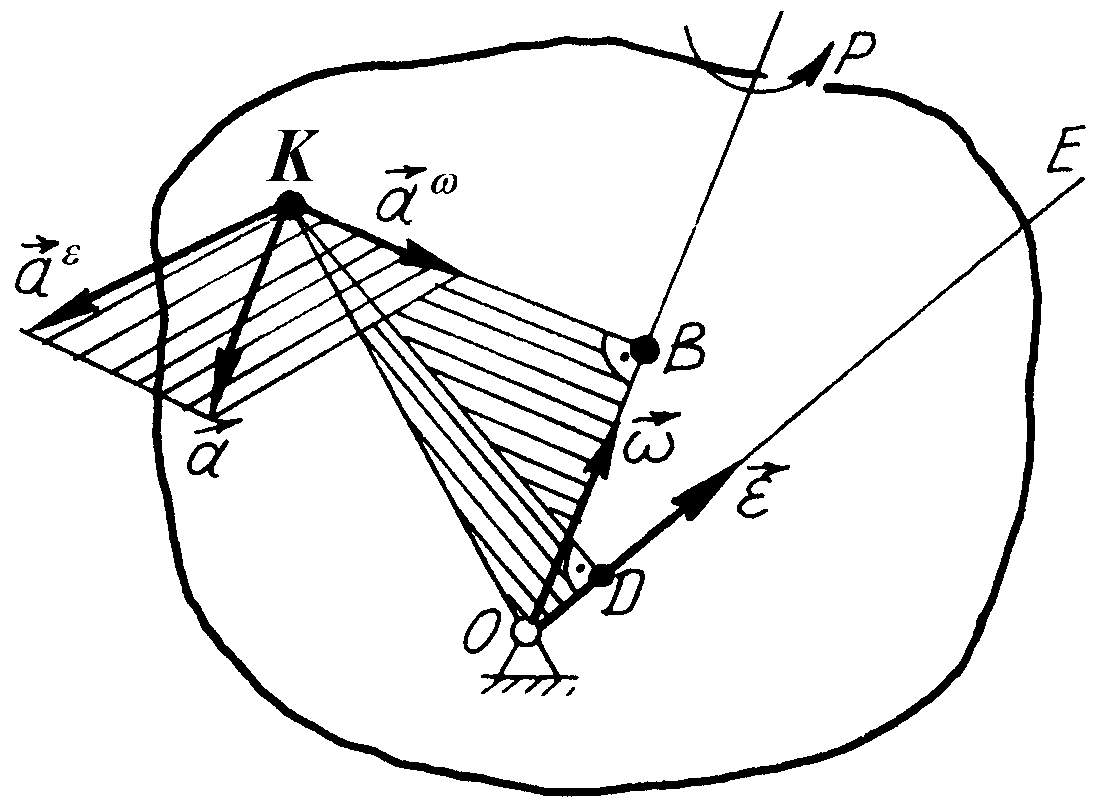
Рис. 143