§ 47.3 Кутова швидкість і кутове пришвидшення тіла, що обертається навколо нерухомої точки

Оскільки обертання тіла навколо нерухомої точки в кожний момент часу можна вважати обертанням навколо миттєвої осі, то

кутова швидкість, з якою в кожний момент часу тіло, що має нерухому точку, обертається навколо миттєвої осі, називається кутовою швидкістю тіла в даний момент часу.

В

Рис. 137

ектор кутової швидкості відкладається з нерухомої точки вздовж миттєвої осі обертання в той бік, звідки обертання тіла видно проти руху годинникової стрілки (рис. 137).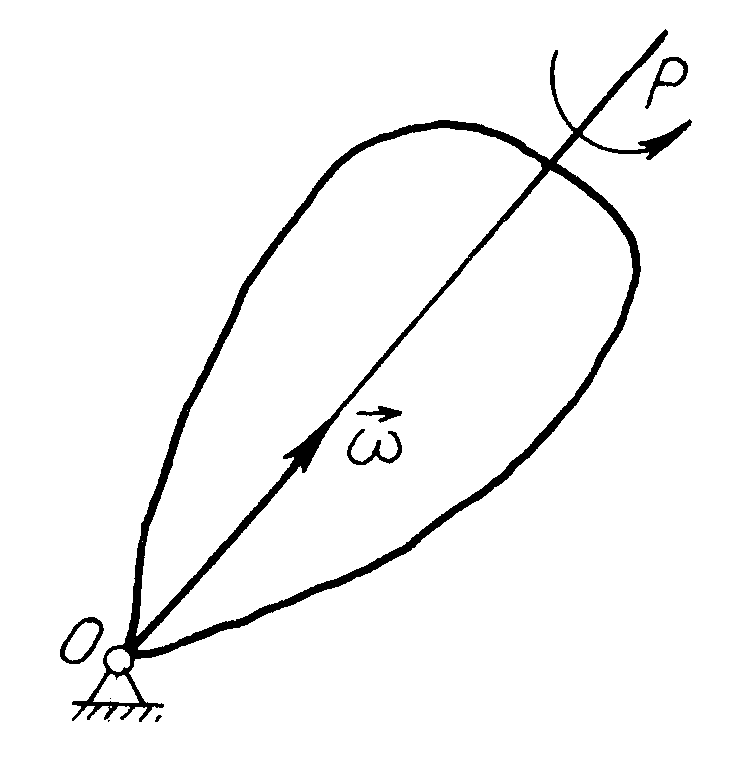

Оскільки при русі точки навколо нерухомої точки не існує такого кута як функції часу, похідна від якого дорівнювала б кутовій швидкості, то кутова швидкість повинна бути задана як функція часу або вона може бути представлена через кути Ейлера і їх похідні.

Як було показано в § 47.1, при русі тіла з однією закріпленою точкою воно одночасно обертається навколо трьох осей, що перетинаються (рис. 138), з кутовими швидкостями ; і .

При такому русі тіла, як буде показано в § 49.3, формула (2.103), вектор результуючої миттєвої кутової швидкості дорівнює

. (а)

Для знаходження величини і напряму вектора кутової швидкості визначимо його проекції на осі рухомої системи координат .

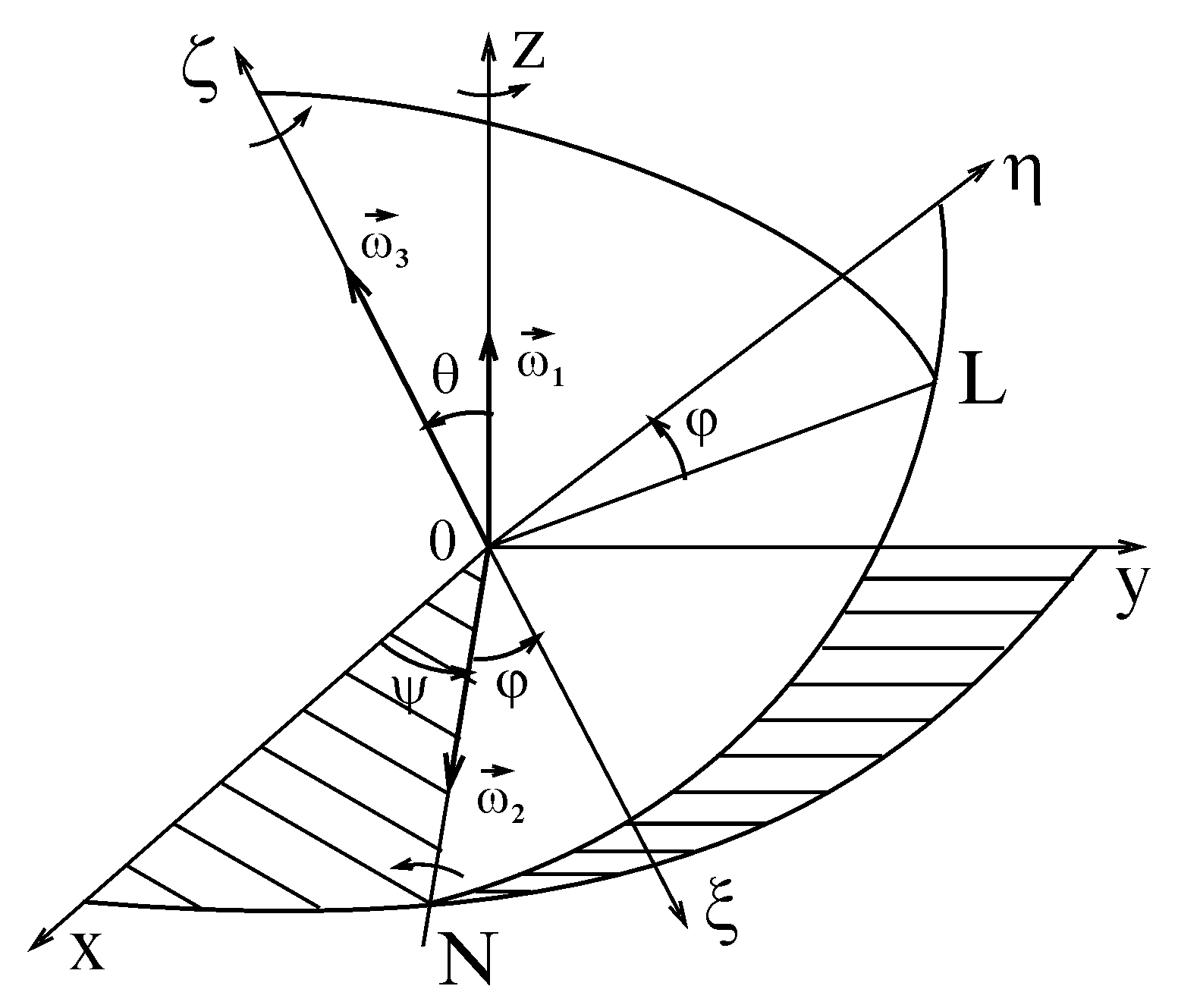
Рис. 138

Проектуючи обидві частини рівності (а) на осі , , , отримаємо

;

; (б)

.

Проекції векторів і знаходяться безпосереднім проектуванням (рис. 138)

; ; ;

; ,

а для знаходження проекції вектора проведемо через осі і площину, яка перетнеться з площиною вздовж лінії . Оскільки лінія вузлів перпендикулярна до площини , то вона перпендикулярна і до лінії , а . Тоді, проектуючи вектор на площину (проекція лежатиме на лінії ), а одержану проекцію, в свою чергу, на осі і , отримаємо

.

Підставляючи одержані проекції в праві частини рівностей (б), отримаємо

;

; (2.78)

.

Аналогічно проектуючи рівність (а) на осі нерухомої системи координат , знайдемо проекції вектора на ці осі

;

; (2.78 а)

.

Рівності (2.78) і (2.78 а) називаються кінематичними рівняннями Ейлера. Вони дають можливість знайти модуль миттєвої кутової швидкості і напрямні косинуси вектора з відповідними осями координат

;

; ; ;

; ; .

Перша похідна за часом від вектора кутової швидкості називається вектором кутового пришвидшення

. (2.79)

В

Рис. 139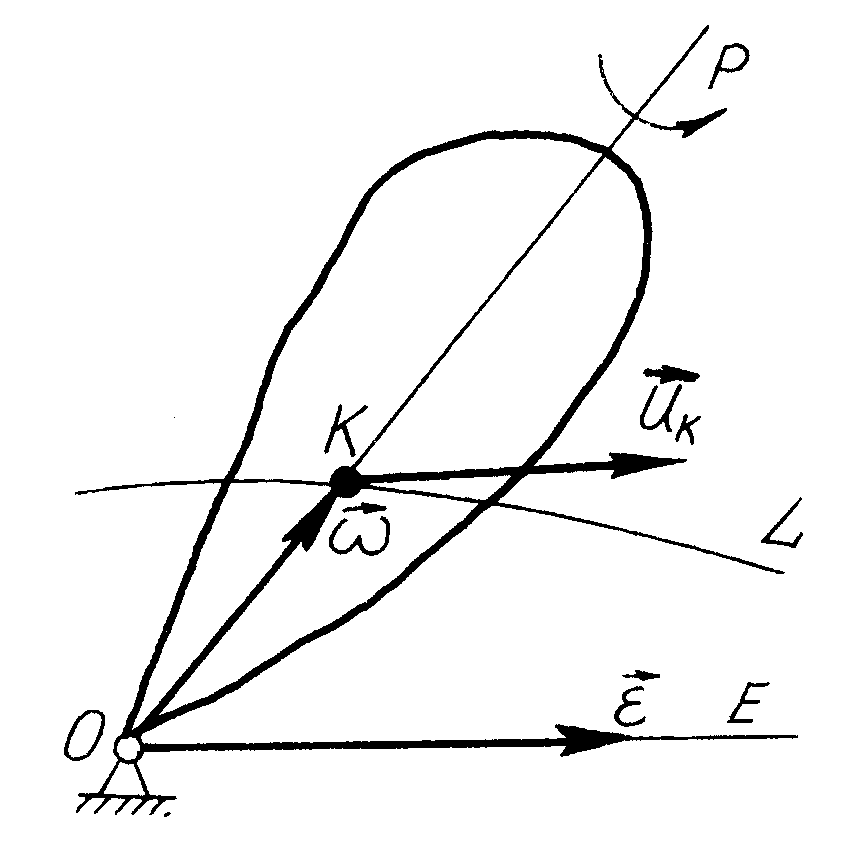

ектор кутового пришвидшення також відкладають з нерухомої точки , навколо якої обертається тіло, але цей вектор (на відміну від обертання тіла навколо нерухомої осі) не буде напрямлений вздовж миттєвої осі обертання, бо кутова швидкість тіла, яке обертається навколо нерухомої точки, може змінюватись як за величиною, так і за напрямом.

Напрям і величину вектора кутового пришвидшення можна знайти таким способом. Позначимо (рис. 139) кінець вектора кутової швидкості буквою К. Оскільки вектор з часом змінює свою величину і напрям, то точка переміщається з часом у просторі, описуючи деяку криву (рис. 139), яка називається годографом век-тора кутової швидкості.

Вектор визначає положення точки в просторі, отже для даної точки він є радіусом-вектором, а це означає, що

, (в)

де – вектор швидкості точки , який, як відомо, напрямлений вздовж дотичної до траєкторії руху точки.

Порівнюючи (2.79) і (в), робимо висновок, що

, (2.80)

тобто:

вектор кутового пришвидшення тіла, котре обертається навколо нерухомої точки, геометрично до-рівнює вектору швидкості точки, яка описує годо-граф вектора кутової швидкості.

Отже, вектор кутового пришвидшення , який, як було сказано вище, відкладається з нерухомої точки, є паралельним вектору , котрий напрямлений вздовж дотичної до годографа вектора кутової швидкості (рис. 139). Рівність (2.80) часто використовують для визначення кутового пришвидшення тіла, яке обертається навколо нерухомої точки. Для цього, використовуючи відомі способи, визначають величину і напрям вектора швидкості, який описує годограф вектора кутової швидкості. Величина і напрям вектора визначає величину і напрям вектора .

Пряму (рис. 139), вздовж якої напрямлений вектор , можна назвати миттєвою лінією кутового пришвидшення.

Величину і напрям кутового пришвидшення можна також знайти аналітично за допомогою формул

;

; ; ;

; ; ,

де ; ; ; ; ; .