§ 47.1 Кути Ейлера. Рівняння обертання твердого тіла навколо нерухомої точки

Нехай точка О (рис. 133) є нерухомою і навколо неї обертається деяке тверде тіло. Розмістимо в цій точці початок двох декартових систем координат: нерухомої Оxyz і рухомої , які незмінно пов’язані з твердим тілом. Оскільки рухо-ма система координат жорстко з’єднана з твердим тілом, то її положення однозначно визначатиме положення тіла і навпаки. Лінію перетину нерухомої координатної площини Оxy і рухомої позначимо ON. Ця лінія називається лінією вузлів. Введемо такі позначення

(псі), (фі) , (тета) ,

причому вважаємо кути додатними у тому випадку, якщо для спостерігача, що дивиться відповідно з боку додатних осей Oz, і лінії вузлів ON, ці кути здаються відкладеними від відповідних осей Оx, ON і Oz в бік, протилежний обертанню годинникової стрілки, як вказано на рис. 133.

Рис. 133

Заданням кутів однозначно визначається положення осей , отже і положення тіла. І дійсно:

1. Відклавши в нерухомій координатній площині кут , як вказано на рис. 133, отримаємо положення лінії вузлів ON.

2. Провівши перпендикулярно до лінії вузлів ON через вісь Oz площину і відклавши в цій площині кут , як вказано на рис. 133, отримаємо положення осі .

3. Якщо через лінію вузлів перпендикулярно до осі провести площину і в заданій площині від лінії вузлів ON відкласти кут , як вказано на рис. 133, то отримаємо положення осі . Вісь знаходиться в цій же площині і складає разом з осями і праву систему координат.

Таким чином, кути повністю, до того ж однозначно, визначають положення рухомої системи. Кути називаються кутами Ейлера. Крім того, кожний з них має свою назву, що визначається обертанням, яке буде здійснювати тіло при зміні відповідного кута. Так, кут називається кутом власного обертання, бо при зміні цього кута тіло обертається, як вказано на рис. 134, навколо осі . – це кут прецесії. При зміні цього кута тіло обертається (див. рис. 134) навколо осі Oz, тобто вісь обертається (прецесує) навколо осі Oz. – називається кутом нутації. При зміні даного кута тіло обертається, як вказано на рис. 134, навколо лінії вузлів ON.

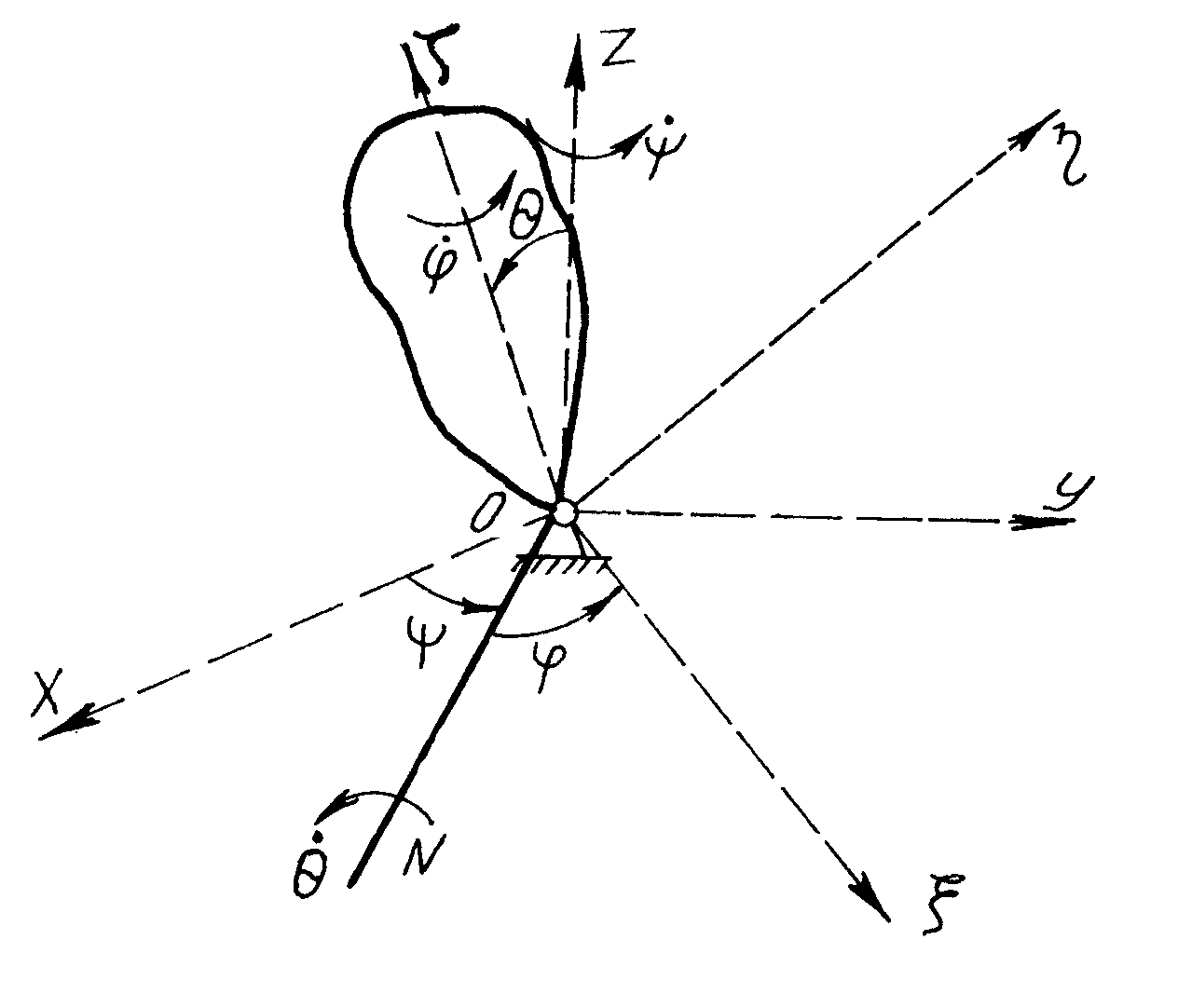
Рис. 134

Якщо тверде тіло виконує обертальний рух навколо нерухомої точки О, то кути безперервно змінюються з часом, тобто є деякими функціями часу

; ; . (2.77)

Записані рівняння, що цілком визначають обертальний рух твердого тіла навколо нерухомої точки, називаються кінематичними рівняннями руху твердого тіла навколо нерухомої точки. Вони визначають закон руху тіла.

§ 47.2 Теорема Ейлера-Даламбера

Як видно з попереднього, обертання тіла навколо нерухомої точки складається з обертань трьох осей . Виходячи з цього, можна отримати відповідні формули для визначення кінематичних характеристик руху тіла і його точок. Отримати дані формули можна і іншим шляхом. Для цього розглянемо теорему Ейлера-Даламбера:

усяке переміщення твердого тіла, що має одну нерухому точку, можна здійснити шляхом одного повороту навколо деякої осі, що проходить через нерухому точку.

Д

Рис. 135

Рис. 136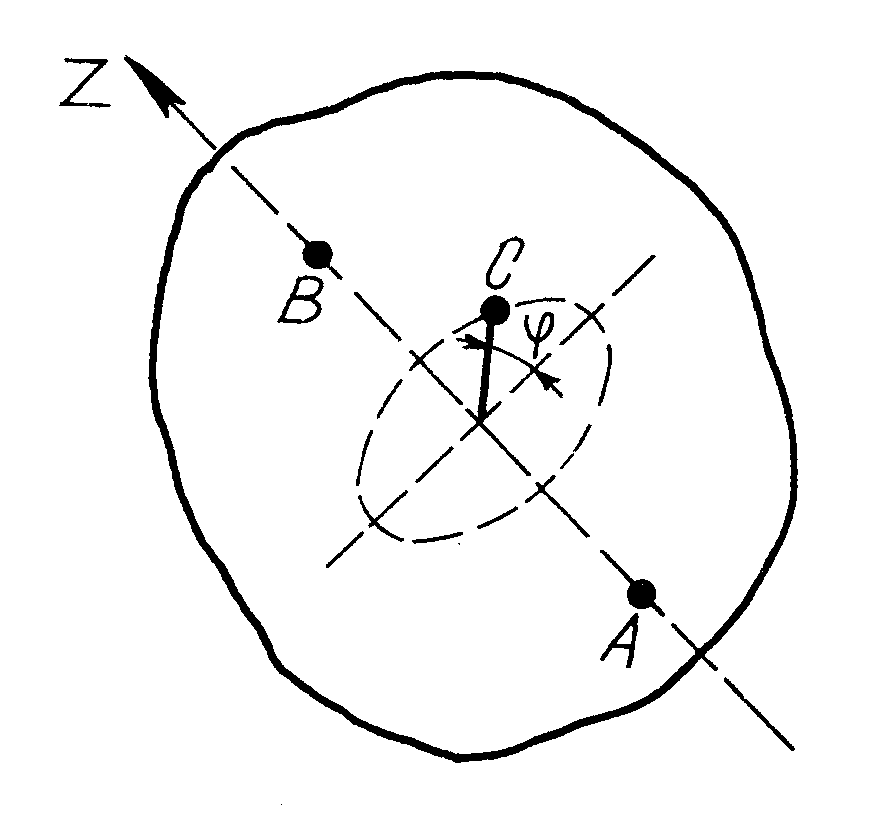

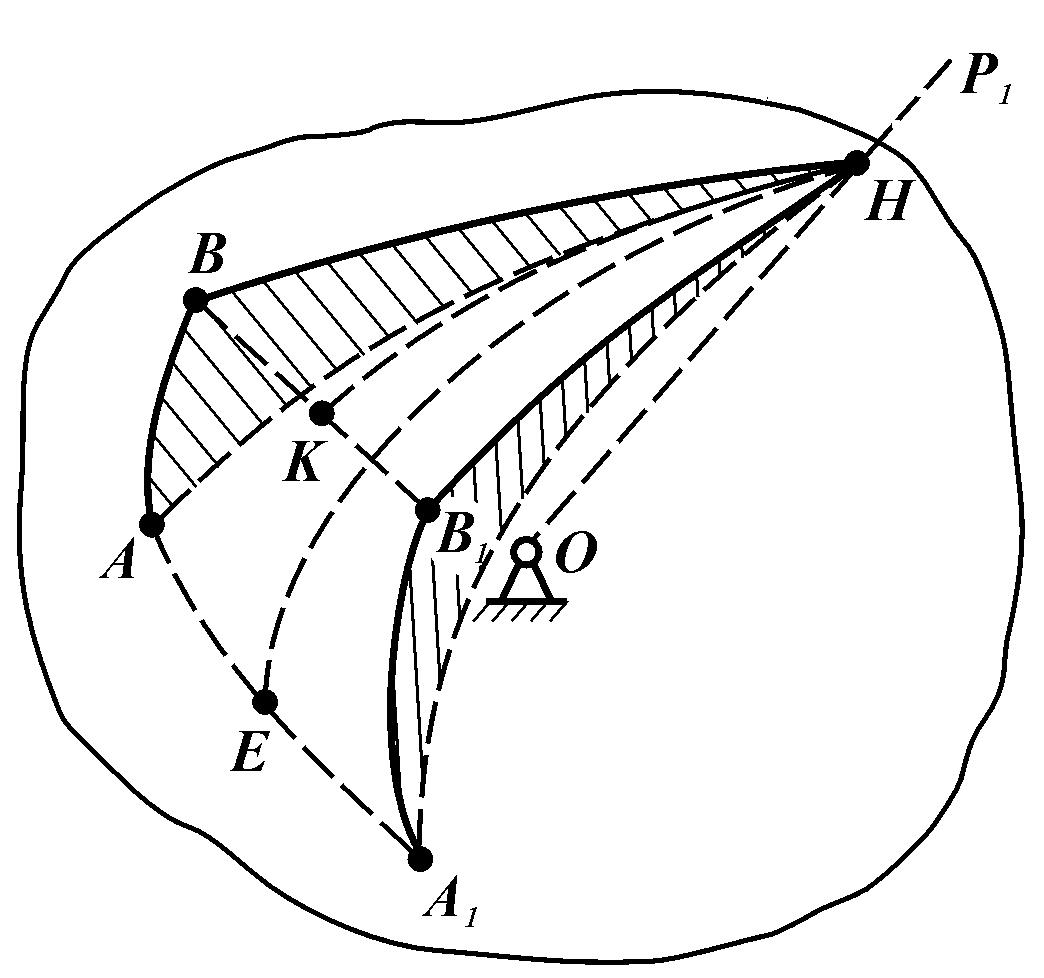
ля доведення даної теореми зауважимо, що положення твердого тіла в просторі однозначно визначається положенням трьох його точок, які не лежать на одній прямій. І дійсно (рис. 135), положення двох точок А і В тіла визначає положення деякої осі тіла Аz, а положення третьої точки С – кут повороту тіла відносно даної осі. До того ж при закріпленні даних точок тіло стане нерухомим, тобто займе деяке конкретне положення, що є ще одним підтверд-женням, що положення тіла в просторі цілком визначається положенням трьох його точок.

Перейдемо тепер до доведення сформульованої вище теореми. Для цього розглянемо деяке тверде тіло, яке обертається навколо нерухомої точки О (рис. 136). Положення тіла будемо визначати положенням трьох його точок: О – нерухома точка; А і В – дві довільні точки тіла, що знаходяться від нерухомої точки на однаковій відстані (ОА=ОВ), але не лежить з нею на одній прямій. Проведемо через ці точки сферу з центром в точці О.

Через точки А і В проведемо дугу великого кола (дуга великого кола – це дуга кола, центр якого знаходиться в нерухомій точці О). Оскільки точка О нерухома, то положення тіла буде визначатись положенням дуги .

Припустимо, що в момент часу тіло займає положення , а в момент часу – положення , тобто за деякий проміжок часу тіло перемістилось з положення в положення . Проведемо дуги і великих кіл. Через точки Е і К, які ділять відповідно і навпіл, проведемо перпендикулярно до даних дуг дуги великих кіл. Позначимо Н точку перетину щойно проведених дуг і з’єднаємо її дугами великих кіл з точками А, В, А₁, В₁. Отримаємо (на рис. 136 вони заштриховані) сферичні трикутники АВН і А₁В₁Н, які є рівними за рівністю трьох сторін:

, бо в твердому тілі відстані між точками зберігаються;

– це випливає з рівності сферичних прямокутних трикутників АЕН і А₁ЕН, в яких сторона ЕН є спільною – за побудовою;

– це випливає з рівності сферичних прямокутних трикутників ВКН і В₁КН, в яких сторона КН є спільною, а – за побудовою.

В рівних трикутниках відповідні кути є рівними, отже

.

Додаючи до обох частин цієї рівності по куту , отримаємо

або

.

Отже, при переміщенні тіла з положення АВ в положення для суміщення точок з і з достатньо здійснити обертальний рух на один і той же кут , а це означає, що все тіло як одне ціле повернуте на той же кут . При такому повороті залишаються нерухомими дві точки: точка О і точка Н. Вісь , яка проходить через ці точки, також буде нерухомою. Таким чином, переміщення тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі на кут . Вісь називається віссю кінцевого повороту, а кут – кутом кінцевого повороту.

Якщо усяке переміщення твердого тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі кінцевого повороту, то, очевидно, і нескінченно мале його переміщення також може бути здійснене таким чином. При наближенні нескінченно малого переміщення до нуля положення тіла наближається до його першого положення. Разом з тим вісь наближається до деякого граничного положення , яке називається миттєвою віссю обертання для заданого моменту часу.

Отже, в кожний момент часу обертання твердого тіла навколо нерухомої точки можна розглядати як обертання навколо миттєвої осі, яка проходить через нерухому точку.

Для кожного моменту часу миттєва вісь обертання займає своє положення, і з часом описує конічну поверхню.

Конічна поверхня, яка описується миттєвою віссю обертання в нерухомому просторі (в просторі системи координат Оxyz), називається нерухомим аксоїдом.

Конічна поверхня, яка описується миттєвою віссю обертання в рухомому просторі (в просторі системи координат O ), називається рухомим аксоїдом.

При обертанні тіла навколо нерухомої точки рухомий аксоїд, змінюючи своє положення, рухається по поверхні нерухомого аксоїда.