§ 46.5 Миттєвий центр швидкостей

Точка твердого тіла під час плоского руху, швидкість якої в даний момент часу дорівнює нулеві, називається миттєвим центром швидкостей.

Миттєвий центр швидкостей найчастіше позначається буквою Р або . Отже, . Користуючись формулою (2.65),покажемо, що в усякий момент часу існує точка плоскої фігури, швидкість якої в даний момент часу дорівнює нулеві.

Д

Рис. 119

ля цього розглянемо плоску фігуру, яка виконує деякий рух у площині рисунка (рис. 119). За полюс плоскої фігури візьмемо точку О, швидкість якої . Нехай навколо полюса плоска фігура обертається так, як вказано на рис. 119. З точки О перпендикулярно до проводимо промінь ОВ в бік, який співпадає з напрямом обертання плоскої фігури. На цьому промені на відстані візьмемо точку Р і за формулою (2.65) визначимо її швидкість

. (а)

Обертальна швидкість точки Р навколо полюса О за величиною дорівнює

,

а напрям вектора цієї швидкості, який перпендикулярний до ОР і напрямлений в бік обертання, як видно з рисунка 119, протилежний напряму вектора швидкості . Враховуючи це, отримуємо, що векторна сума (а) перетворюється в алгебраїчну різницю, яка дорівнює

.

Отже, для плоскої фігури в кожний момент часу є миттєвий центр швидкостей.

З доведення даного твердження випливає, що:

1. Миттєвий центр швидкостей плоскої фігури знаходиться на промені, перпендикулярному до вектора швидкості полюса.

2. Відстань до миттєвого центра швидкостей визначається за формулою

. (67)

Припустимо тепер, що миттєвий центр швидкостей Р взято за полюс плоскої фігури (див. формулу 2.65)

і, враховуючи, що швидкість полюса в даному випадку дорівнює нулеві ( ), отримаємо такий результат:

. (2.68)

Швидкість будь-якої точки плоскої фігури є обертальною швидкістю навколо миттєвого центра швидкостей

З отриманого результату випливає:

1. Оскільки , то і .

Оскільки К – довільна точка плоскої фігури, то маємо, що

вектори швидкостей точок плоскої фігури перпендикулярні до відрізків, що з’єднують відповідні точки з миттєвим центром швидкостей.

2. За формулою обертальної швидкості з (2.68) отримуємо

. (2.69)

Швидкість будь-якої точки плоскої фігури чисельно дорівнює добутку кутової швидкості на відстань даної точки до миттєвого центра швидкостей.

3. Формулу (2.69) можна застосувати для визначення швидкості будь-якої точки плоскої фігури. Для точок А, В і С матимемо

,

,

.

Звідси отримуємо, що

. (2.70)

Швидкості точок плоскої фігури пропорційні відстаням даних точок до миттєвого центра швидкостей. Коефіцієнт пропорційності дорівнює кутовій швидкості плоскої фігури.

Формули (2.68)-(2.70) визначають швидкості точок плоскої фігури за допомогою миттєвого центра швидкостей. На основі цих формул можна зобразити розподіл (еп’юр) швидкостей точок плоскої фігури. Цей розподіл має вигляд, який зображений на рис. 120. На цьому рисунку показано: Р – миттєвий центр швидкостей плоскої фігури; вектори швидкостей точок плоскої фігури, які перпендикулярні до відрізків, що з’єднують відповідні точки з миттєвим центром швидкостей; величини їх пропорційні відстаням даних точок до миттєвого центра швидкостей. Цей розподіл відповідає розподілу швидкостей точок тіла, яке обертається навколо нерухомої осі, т

Рис. 120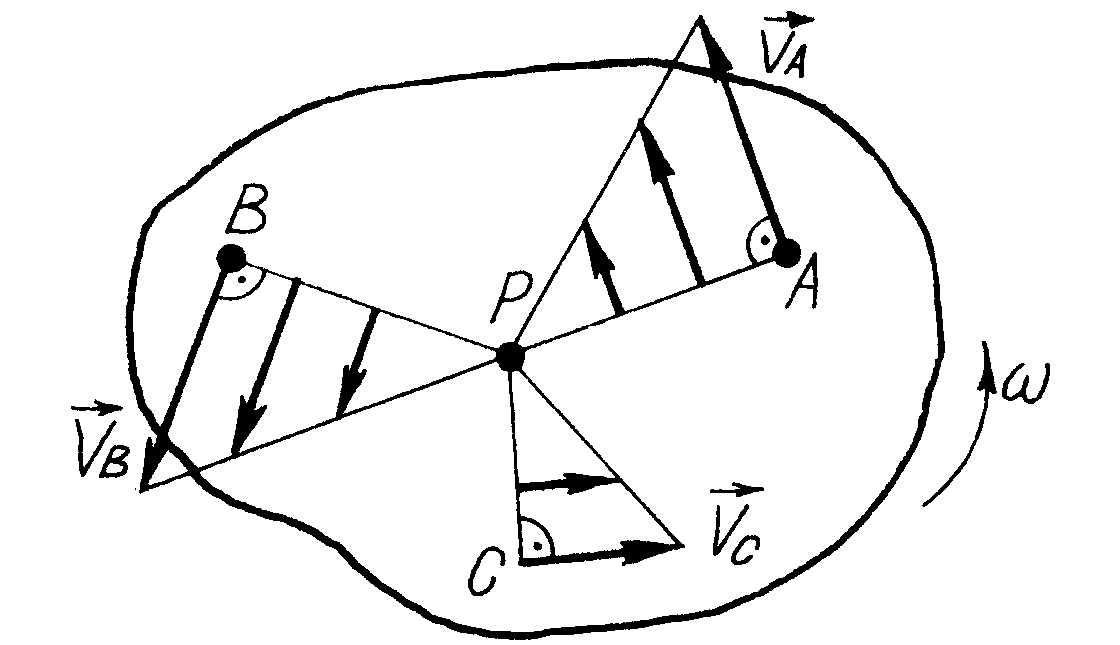

обто, в кожний момент часу швидкості точок плоскої фігури розподілені так, немов би фігура обертається навколо точки Р. Саме тому миттєвий центр швидкостей плоскої фігури називають миттєвим центром її повороту. До того ж є відповідна теорема (див. теорему Шаля), згідно з якою:

1. Плоску фігуру можна перемістити з одного положення в будь-яке інше шляхом одного повороту навколо деякої точки, яка називається центром повороту.

2. Граничне положення центра повороту, тобто положення центра повороту для нескінченно малого переміщення плоскої фігури, є не що інше, як миттєвий центр швидкостей плоскої фігури.