3.1 Закон збереження імпульсу
З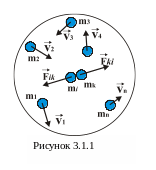
акони
Ньютона настільки потужні фундаментальні
закони, що з них випливають інші
фундаментальні закони, одним з яких є
закон збереження імпульсу. Цей закон
справедливий для, так званої, замкнутої
системи, тобто такої, на тіла якої не
діють зовнішні сили або їх рівнодійна
дорівнює нулю.
Тіла можуть
діяти тільки між собою – ці сили називають
внутрішніми. Нехай замкнута система
складається з
частинок, які рухаються з різними
швидкостями і стикаються між собою, не
виходячи за межі замкнутої системи
(рис.3.1.1). Наприклад, на частинку під
номером
діє сила
зі сторони частинки з номером
і, навпаки, на
-ту
частинку діє сила
.
Запишемо другий закон Ньютона через
зміну імпульсу для кожної частинки,
враховуючи, що на цю частинку можуть
діяти інші частинки:
(
.
(3.1.1)
В цих рівняннях
перший індекс – це номер частинки, на
яку діють інші тіла, другий індекс –
номер частинки, яка діє на частинку з
першим індексом. Звичайно, що двох
однакових індексів не може бути, частинка
сама на себе не діє. Додаючи
рівняння і
враховуючи, що
;
........
будемо мати:
.
(3.1.2)
Це можливо лише тоді, коли під знаком диференціала є стала величина, тобто
.
(3.1.3)
Отримали закон
збереження імпульсу для замкнутої
системи, який стверджує, що геометрична
сума імпульсів частинок замкнутої
системи є величина стала.
Враховуючи позначення
,
цей закон запишеться:
.
(3.1.4)
В основі закону збереження імпульсу лежить однорідність простору, тобто однаковість властивостей простору в усіх його точках. Тут «однаковість» треба розуміти в тому, що паралельне перенесення замкнутої системи з одного місця простору в інший без зміни взаємного розташування і швидкостей частинок не змінює механічних властивостей даної системи. При цьому мається на увазі, що замкнутість системи не порушується.
3.2 Центр мас. Теорема про рух центра мас
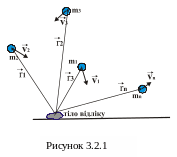В фізиці введення
кожної нової величини завжди обґрунтоване,
немає виводу формули заради виводу. Як
приклад цього покажемо, що для замкнутої
системи, яка складається з матеріальних
точок, доцільно ввести особливу фізичну
величину, яку назвемо центром мас
системи. Наприклад, є
частинок (матеріальних точок), необхідно
математично описати цю систему.
Скористаємось векторним методом опису
руху частинки. Виберемо тіло відліку і
тоді положення кожної точки буде
визначатись „своїм” радіусом-вектором
(рис.
3.2.1).
Таким чином, для
векторного способу даної системи
необхідно мати
рівнянь виду
.
Тоді виникає питання, а чи не можна
спростити математичний опис такої
замкнутої системи і як це зробити.
Відповідь на це треба шукати в тій
величині, яка є сталою для всієї замкнутої
системи, тобто в законі збереження
імпульсу. Запишемо цей закон, враховуючи,
що
,
(3.2.1)
або
.
(3.2.2)
Вираз в дужках є векторна сума, яку можна записати у вигляді
,
(3.2.3)
тобто замість
векторів маємо один вектор
,
який дорівнює
.
(3.2.4)
Цей вектор визначає
положення особливої точки замкнутої
системи, в якій „зібрана” вся маса
системи
.
Ця точка називається центром мас системи.
Ввівши поняття центра мас системи, який визначається вектором 3.2.4 рівняння 3.2.2 прийме простий вигляд
.
(3.2.5)
Т
ак,
як
– швидкість центра мас системи, то вираз
вказує на те, що швидкість центра мас
системи є величина стала, а прискорення,
як похідна від сталої швидкості, дорівнює
нулю. Отже, отримаємо ще одне фундаментальне
твердження про властивість замкнутої
системи –
Теорему про рух центра мас такої системи:
центр мас замкнутої системи під дією внутрішніх сил не може набути прискорення, у відсутності зовнішніх сил він рухається рівномірно прямолінійно або знаходиться в стані спокою.
А тепер згадаємо знаменитого барона Мюнхаузена, який, сидячи на коні, сам себе і коня витягнув з болота, взявшись за чуба (рис.3.2.2). Тобто, під дією внутрішніх сил (тягнув сам себе за чуба), всупереч фундаментальній фізичній теоремі про рух центра мас системи, все ж таки зрушив з місця (з болота) центр мас цієї системи (барон+кінь).
І, як не дивно, в наш час знаходяться послідовники барона Мюнхаузена, які всупереч фундаментальному закону фізики про рух центра мас системи намагаються створити машину, яка б рухалась тільки під дією внутрішніх сил. Тут і нашумівша в один час (1962 рік) машина, створена страховим агентом Діном. Останні спроби створити, так званий, безопорний двигун, який би рухався тільки за рахунок внутрішніх сил, датується 2008 роком. Зайдіть в інтернат на сайт «Безопорные двигатели» і Ви знайдете описи найрізноманітніших технічних конструкцій, які ніби дозволяють пересуватись в просторі всій системі тільки за рахунок зміни внутрішнього стану системи без будь якого відокремлення її частини, як це має місце в ракетних двигунах. Але чомусь ці конструкції не працюють і не будуть працювати, так і ніколи не будуть працювати вічні двигуни. Про неможливість безопорного руху влучно висловився Архімед ще в другому столітті до нашої ери у крилатій фразі – дайте мені точку опори і я підніму Землю. Так ось, всі спроби створити безопорний двигун приречені на невдачу, так само, як неможливо Архімеду без точки опори зрушити Землю.