1.3.2. Зв'язок між кутовими і лінійними кінематичними величинами обертального руху

Важлива практична задача, знаючи кутові кінематичні величини обертового руху, наприклад, кутову швидкість (рад ⁄с,) та прискорення (рад ⁄с²), перейти до лінійних величин (м ⁄с та м ⁄с²). Наприклад, точка тіла, яке обертається, знаходиться на відстані r від осі обертання. За час радіус повернеться на кут , а точка пройде дугу рис. 1.3.3.

Тоді лінійна швидкість визначиться, як похідна від шляху по часу, а враховуючи, що будемо мати

, (1.3.13)

тобто отримали в скалярній формі зв’язок між лінійною та кутовою швидкостями. Тепер встановимо цей зв’язок у векторній формі. Наприклад, точка рухається по колу і її положення задається радіусом-вектором. Лінійна швидкість, як вектор, дотична до кола, а напрям вектора кутової швидкості, як вказано на рис. 1.2.2.2 визначається за правилом правого гвинта.

Як видно з рис. 1.3.2., маємо трійку перпендикулярних векторів і згідно правил векторної алгебри можливий лише один векторний добуток

. (1.3.14)

Якщо при обертальному русі має місце кутове прискорення , то це приводить до зміни лінійної швидкості, до появи тангенціального прискорення , зв’язок між якими легко встановити. Враховуючи, що , а , то при , будемо мати

. (1.3.15)

Між рівняннями кінематики поступального та обертального рухів існує аналогія. Так, якщо для поступального руху тіла залежність шляху S від часу t задається відповідним рівнянням , то кінематичне рівняння обертового руху визначає залежність кута повороту φ від часу t, тобто . Потім, якщо лінійна швидкість – похідна від шляху по часу, то кутова швидкість – похідна від кута повороту від часу і т.д. На сторінці…. наведено порівняльну таблицю лінійних і кутових кінематичних величин.

1.4 Кінематика відносного руху. Переносне прискорення. Прискорення каріоліса

Вводячи поняття швидкості та прискорення ми «по замовчуванню» вважали, що система відліку, де знаходиться дане тіло є нерухомою. Така система, як буде вказано згодом, називається інерціальною (див. розділ 2). А що буде коли вибрана нами система рухається відносно іншої системи? Таке питання має надзвичайно важливе практичне значення і відповідь на поставлене питання дає кінематика відносного руху. А тепер така кінематика відносного руху у жанрі відомого бойовика про Джеймса Бонда – секретного агента 007, який виходить цілим збудь яких перепалок. Так ось, гангстерам все ж таки вдалось упіймати Джеймса і запроторити його в залізний ящик і кинути з крутої скелі. Далі все як у справжньому бойовику. Агент 007 все ж таки в останній момент встигає вибратись з ящика і на нього вже чекає човен (ви його бачите біля підніжжя скелі) та чарівна блондинка. А тепер все з точки фізики. Скеля – це тіло відліку, з яким зв’язують систему координат XYZ. Будемо вважати таку систему відліку нерухомою (спробуйте зрушити скелю). Залізний ящик і зв’язана з ними система координат X´Y´Z´ утворюють рухому систему відліку, де перебуває Джеймс Бонд, якого ми (вибачте, агент) вважаємо матеріальною точкою Р (рис 1.4.1).

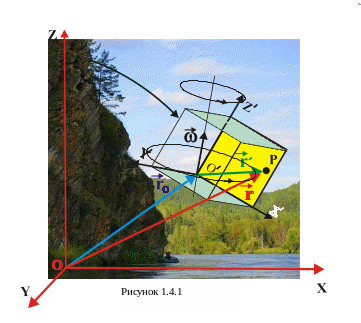
У кінематиці відносно вибрану за нерухому систему відліку називають основною системою, відносно якої рух тіла або матеріальної точки вважаємо абсолютним рухом, а швидкість будь якої точки відносно даної системи називають абсолютною швидкістю.

Положення точки Р в просторі відносно основної системи відліку визначається радіусом – вектором (див. рис.1.4.1). Тоді абсолютна швидкість цієї точки буде першою похідною від такого вектора переміщення по часу

. (1.4.1)

Відносно системи X´Y´Z´ положення точки Р визначається радіусом вектором . Що стосується самої системи X´Y´Z´, то її початок (точка О´) задається вектором . Легко бачити, що

. (1.4.2)

Тоді згідно (1.2.3.1) можна записати

. (1.4.3)

Таким чином, абсолютна швидкість точки дорівнює векторній сумі двох швидкостей. Перший доданок визначає швидкість відносно рухомої системи тому, така швидкість отримала назву відносна швидкість

. (1.4.4)

Другий доданок, що визначає швидкість рухомої системи називають переносною швидкістю

. (1.4.5)

Отже, абсолютна швидкість точки дорівнює сумі її переносної та абсолютної швидкостей

. (1.4.6)

Цей результат, який, правда, без математичного доведення передбачив Галілей, називають галілеєвим законом додавання швидкостей. Особливо цей закон є самоочевидним, коли швидкості напрямлені по одній прямій (див. Приклади задач з додаванням швидкостей – човен за течією ріки або проти).

Поки що зі швидкостями ніби все вияснили. А тепер що буде у випадку зміни швидкостей, у випадку прискорень.

Похідна від абсолютної швидкості по часу буде, відповідно, визначати абсолютне прискорення

. (1.4.7)

Тобто, повне прискорення дорівнює сумі відносного та переносного прискорень

. (1.4.8)

В найбільш простому випадку, коли переносне прискорення відсутнє , тоді абсолютне прискорення дорівнює відносному. Це можливо тоді, коли система відліку переребуває стані спокою або приймає участь в рівномірному прямолінійному русі. Ніби простий, але дуже важливий результат: прискорення тіла є однаковим в усіх системах відліку, які рухаються одна відносно іншої з сталою швидкістю або знаходяться в стані спокою. Забігаючи наперед, ми майже сформулювали механічний принцип відносності Галілея, згідно якого всі закони механіки однакові в усіх інерціальних системах відліку, тобто які є в стані спокою або рухаються зі сталою швидкістю (див. розділ… ).

А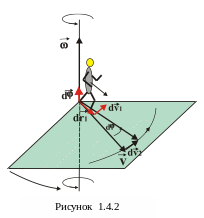 що буде, коли система X',Y,'Z', як це вказано на рис.1.4.2 обертається і в цій системі рухається тіло? Напевне Ви відчували щось особливе, коли обертаючись на каруселі намагались пересісти з одного місця на інше, Вас кудись «заносило» в сторону. В курсах теоретичної механіки та в курсах фізики спеціально для фізиків наводиться строгий математичний вивід кінематики такого руху і встановлюється, що тіло, яке рухається зі швидкістю v в системі, яка обертається з кутовою швидкістю ω зазнає особливого прискорення. Це прискорення отримало назву каріолісового прискорення (фр. учений Каріоліс) і вектор цього прискорення дорівнює

(1.4.9)

А тепер спробуємо отримати значення цього прискорення, звертаючи основну увагу на фізику явища з мінімумом математики. Хоча такий вивід не буде строго математичним, але дасть змогу вияснити – чому саме при русі тіла в системі, що обертається виникає особливе прискорення і це особливе прискорення зовсім немає відношення до нормального (доцентрового ) прискорення.

Отже, Ви (вже не Джеймс Бонд) знаходитесь в центрі системи, що обертається – на самому краю дна ящика (не хвилюйтесь, ніхто ящик кидати не буде, з таким же самим успіхом можна навести приклад з каруселлю, де Ви намагаєтесь рухатись подалі від центра).

Якщо Ви зробили від центра крок довжиною вздовж радіуса кола, «кінчик» цього вектора почав обертатись, адже система обертається. Швидкість обертового, а не поступального руху вашої ноги, де знаходиться кінчик вектора зросла на . Використовуючи зв'язок між лінійною та кутовою швидкостями можна записати

. (1.4.10)

Якщо тривалість кроку , то зміна швидкості за час буде визначати прискорення, яке перпендикулярне до напряму вашого руху і не напрямлене до центра

. (1.4.11)

А що визначає похідна від по часу ? Звичайно – швидкість Вашого руху (строго кажучи, швидкість матеріальної точки, що рухається по прямій від центра обертання). Тому

. (1.4.12)

Але це ще не все, сам вектор швидкості за час повертається на кут і тоді зміна швидкості за напрямом викликана таким поворотом як (елементарна дуга кола) дорівнює

, (1.4.13)

так як

, (1.4.14)

то

. (1.4.15)

Похідна по часу дає ще одне значення прискорення

. (1.4.16)

Отже, повне прискорення тіла, що рухаються в обертовій системі відліку дорівнює

. (1.4.17)

Наш вивід не є математично строгим, але розкриває фізичний зміст появи особливого каріолісового прискорення. А саме, якщо матеріальна точка рухається зі швидкістю в системі координат, що обертається з кутовою швидкістю , то: