2. Перевірка основного рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання.

Фізика – експериментальна наука і її фундаментальні закони є результатом дослідів та спостережень і, звичайно, що ці закони вимагають експериментальної перевірки. Одна із відомих латинських сентенцій (крилатий вираз) говорить «non verte in verbe» – нічого не приймати на слово. Так ось, основне рівняння динаміки обертального руху твердого тіла стверджує, що момент сили , прикладений до тіла з моментом інерції надає цьому тілу кутового прискорення , так що . Це все слова, і навіть формула цього закону виведена на папері, а я нічого не приймаю на слово (латинська сентенція). Тому Вам пропонується задача-експеримент, яка ілюструє експериментальну перевірку основного рівняння динаміки обертального руху твердого тіла відносно нерухомої осі обертання.

Загальне правило для перевірки фізичного закону, записаного у вигляді формули полягає у тому, що експериментальні числові значення величин, які входять у цю формулу, повинні у результаті підстановки приводити до тотожності. Це значить, у межах похибки експерименту: ліва частина рівняння дорівнює числовому значенню правої. Таким чином, для перевірки основного рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання необхідно:

1. Тіло відомої маси та геометрії для розрахунку моменту інерції цього тіла (вимірюються маса та необхідні геометричні величини);

2. Прикласти до тіла відомий момент сили (виміряти його);

3. Виміряти кутове прискорення обертального руху даного тіла під дією прикладеного моменту сили ;

4. Підставити отримані експериментально значення у формулу

(4.9.13)

і зробити відповідні висновки щодо справедливості основного рівняння динаміки обертального руху твердого тіла.

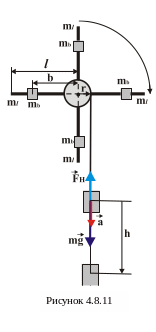Для такої експериментальної перевірки основного рівняння динаміки обертального руху твердого тіла в навчальних фізичних лабораторіях використовують прилад під назвою маятник Обербека, принципова схема якого наведена на рис.4.9.2.1

1. Тілом з відомим моментом інерції є система з чотирьох однакових однорідних стержнів довжиною l та масою m _l кожен. Ці стержні, як видно з рисунку, утворюють хрестовину з одним центром обертання. Вздовж стержнів можна переміщати і зафіксовувати у необхідному положенні на відстані b від осі обертання невеликі тіла масами m _b кожен. Загальний момент інерції такої хрестовини разом з закріпленими на ній тілами дорівнює

(4.9.14)

Пересуваючи тіла вздовж стержнів хрестовини, маємо змогу утворювати тіла обертання з різними моментами інерції, що необхідно для перевірки основного рівняння динаміки обертального руху твердого тіла.

2. Обертовий момент сили M створюється силою натягу нитки, яка намотана на шків (циліндр) радіуса r. До цього шківа (циліндра) прикріплена хрестовина, яка обертається разом з цим шківом. Так як плечем сили натягу нитки є радіус шківа, то момент сили, що обертає хрестовину дорівнює

(4.9.15)

Що стосується значення сили натягу нитки, то ця сила, у свою чергу, створюється вантажем масою m, який прикріплений до нитки, що намотана на шків. На цей вантаж, який опускається вниз з прискоренням а діє сила тяжіння та сила натягу нитки і тоді, згідно другого закону Ньютона, рівнодійна цих сил надає тілу прискорення

(4.9.16)

Як визначити прискорення, як його вимірити ? Для цього звернемось до кінематики руху вантажу, а саме: якщо виміряти відстань, на яку опуститься за час вантаж на нитці, то з рівняння кінематики рівноприскореного руху будемо мати:

. (4.9.17)

Отже,

. (4.9.18)

3. Залишається визначити кутове прискорення обертального руху хрестовини. Знаючи лінійне прискорення ободу шківа та його радіус, з відомого зв’язку між лінійними та кутовими кінематичними величинами обертального руху кутове прискорення визначається простим співвідношенням:

. (4.9.19)

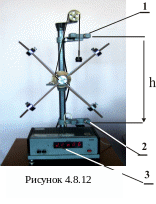Підставивши експериментальні значення моменту сили, моменту інерції та кутового прискорення у рівняння динаміки обертального руху , ми тим самим здійснюємо його перевірку. Така перевірка значно спрощується системою автоматичного вимірювання часу руху вантажу у лабораторній установці (рис.4.9.2.2) маятника Обербека. Вантаж, що опускається, перериває промені світла, які попадають на фотоелементи 1 та 2 і, тим самим, вмикають і вимикають електронний секундомір 3, який дає покази часу руху вантажу.

Поставлену задачу експериментальної перевірки динаміки обертального руху тіла відносно нерухомої осі обертання можна розділити не декілька окремих задач.

1. Маятник Обербека складається з чотирьох однакових однорідних стержнів довжиною 20 см та масою 200 г кожен. На відстані 15 см від центра обертання маятника розташовані і закріплені невеликі вантажі масами 120г кожен. Вважаючи ці вантажі матеріальними точками, визначити момент інерції такого маятника.

Підставляючи всі необхідні числові значення у формулу (4.9.14) отримаємо

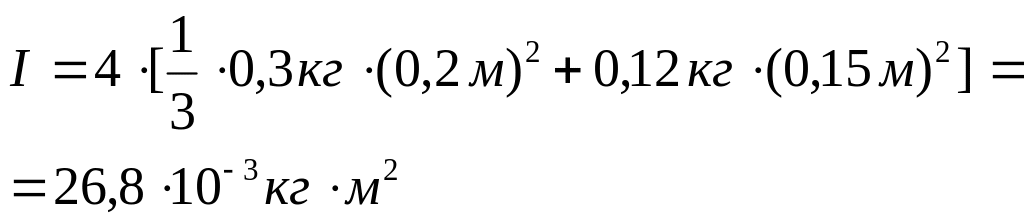. (4.9.20)

2. В досліді з маятником Обербека вантаж на кінці нитки, яка намотана на шків радіуса 2 см за час 1,2с розкручуючи маятник опускається на 40 см. Визначити, яке кутове прискорення обертального руху маятника Обербека.

Спочатку з кінематичної формули рівнозмінного руху знаходимо лінійне прискорення:

. (4.9.21)

Тоді кутове прискорення дорівнює

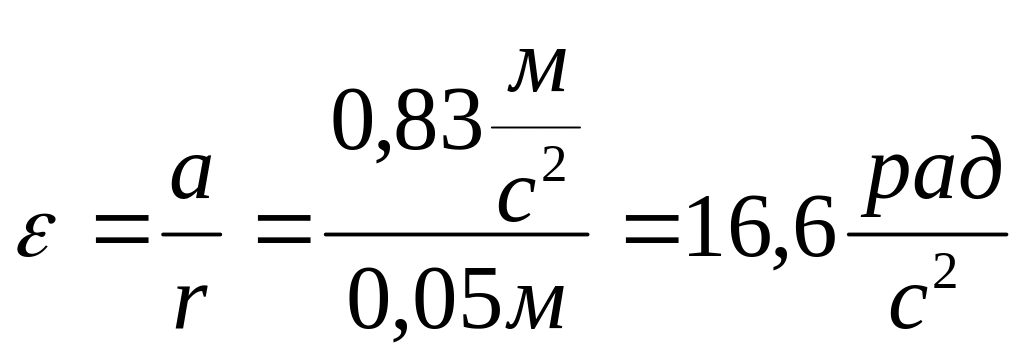. (4.9.22)

3. В досліді з маятником Обербека вантаж масою 40г, підвішений на нитці, яка намотана на шків радіуса 2 см за час 0,8 розкручуючи маятник опускається на 40 см. Визначити момент сили який діє на маятник Обер бека

Використовуючи раніше доведену формулу (4.9.18) та беручи , отримаємо, що момент сили, який обертає маятник Обербека дорівнює

.

4. Перевірка основного рівняння динаміки обертового руху

Отримавши експериментальні значення величин, що входять в основне рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання і підставляючи їх у формулу цього рівняння отримуємо:

(4.9.23)

У той же час, експериментальне значення моменту сили, що надає даному тілу з моментом інерції (маятник Обербека) кутового прискорення , дорівнює . Різниця становить 0,01, що складає 2%. Будь-яке вимірювання фізичної величини не є точним, завжди існує похибка. Тому у межах похибки нашого експерименту справджується основне рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання.

Розглянувши задачу, яка ілюструє застосування основного закону динаміки обертового руху твердого тіла відносно нерухомої осі обертання, необхідно розглянути ще один важливий закон такого руху – закон збереження моменту імпульсу.

3. На горизонтальній круглій платформі (лава Жуковського) знаходиться людина, яка тримає у горизонтальному положенні за його середину однорідний стержень довжиною 3 м та масою 4 кг. При такому положенні (рис.4.8.13(1)) вся система обертається з кутовою швидкістю , яка відповідає одному оберту за секунду. Скільки обертів за одну секунду буде здійснювати така система, якщо людина поверне стержень у вертикальне положення яке співпадає з віссю обертання людини (рис.4.8.13(2))? Круглу платформу та людину, яка стоїть на ній, вважати однорідним суцільним циліндром радіусом 20 см та масою 80 кг.

Вважаючи дану систему замкнутою, можна застосувати закон збереження моменту імпульсу:

, (4.9.24)

де – момент інерції системи, коли стержень у горизонтальному положенні,

момент інерції системи у вертикальному положенні стержня.

Відповідно, та – кутові швидкості системи у першому та другому положення стержня.

У першому, горизонтальному, положенні стержня загальний момент інерції такої системи дорівнює сумі моментів інерції однорідного диску та однорідного стержня:

. (4.9.25)

Якщо стержень знаходиться у вертикальному положенні, так що його вісь співпадає з віссю обертання циліндра, яким ми «замінили» людину на лаві Жуковського, то, вважаючи радіус стержня значно меншим радіуса циліндра, моментом інерції стержня можна нехтувати. Тобто, практично у вертикальному положенні стержня момент інерції системи дорівнює тільки моменту інерції циліндра (людині на лаві Жуковського):

(4.9.26)

Підставивши значення цих моментів інерції, отримаємо, що у вертикальному положенні стержня модуль кутової швидкості даної системи дорівнює:

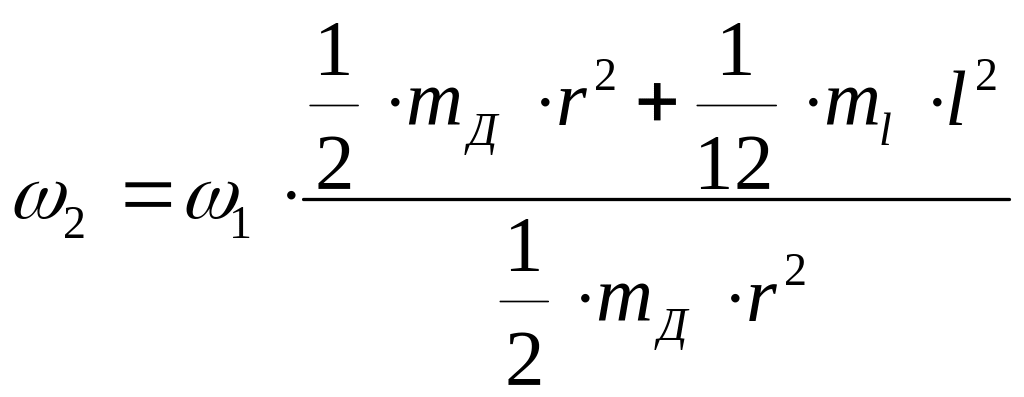. (4.9.27)

Враховуючи зв'язок між кутовою швидкістю і частотою обертання

, отримаємо значення частоти обертання даної системи, коли стержень розташували у вертикальному напрямі:

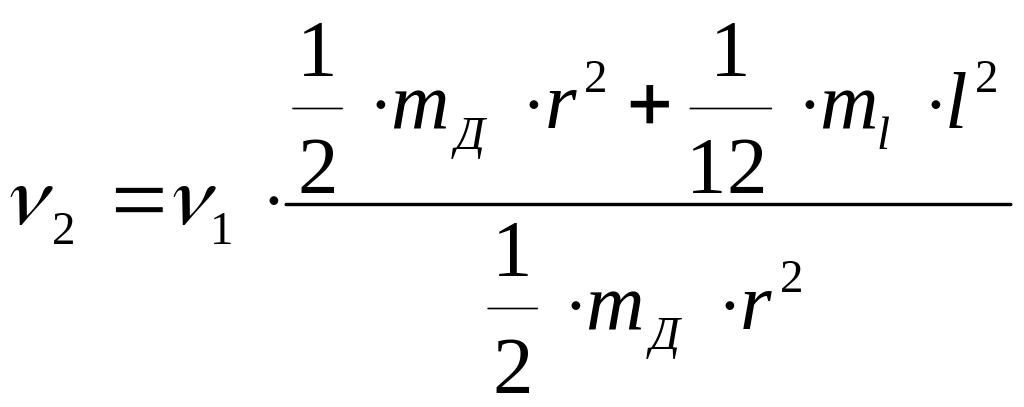(4.9.28)

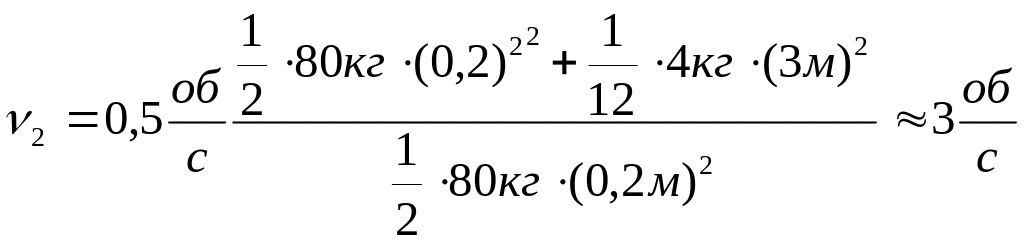(4.9.29)

Розглянута задача є наглядною ілюстрацією закону збереження моменту імпульсу. Дійсно, у першому положенні з більшим моментом інерції системи маємо невелику частоту обертання. Поставивши стержень у вертикальне положення, момент інерції системи зменшується, але, згідно закону збереження моменту імпульсу, добуток кутової швидкості на момент інерції системи є величина стала. Отже, зменшення моменту інерції даної системи (зміна положення стержня) привела до збільшення кутової швидкості.

Розглядаючи закон збереження механічної енергії у випадку обертального руху у багатьох випадках треба враховувати особливості такого руху, коли, крім енергії обертального руху, має місце ще кінетична енергія поступального руху, про що вказувалась у розділі 4.1 (див.рис.4.1.2). Прикладом такого руху, де необхідно враховувати кінетичні енергії обертового та поступального рухів є наступна задача.

4. На вершині похилої площини знаходяться однорідна куля та тонке кільце, як це вказано на рис.4.9.5.1. Тіла відпускають з однакової висоти і вони скочуються вниз по похилій площині. Яка різниця швидкостей цих тіл біля основи похилої площини?

Тіло масою m на висоті h у полі тяжіння Землі володіє потенціальною енергією

, (4.9.30)

яка при подальшому русі вниз по похилій площині перетворюється у кінетичну енергію. Якщо момент інерції дорівнює , то кінетична енергія такого тіла дорівнює сумі кінетичної енергії поступального руху (енергії центра мас тіла), кінетичної енергії обертального руху . Згідно закону збереження і перетворення енергії, можна записати

(4.9.31)

Використовуючи зв'язок між лінійною та кутовою швидкостями , останнє рівняння прийме інший вигляд

, (4.9.32)

звідки

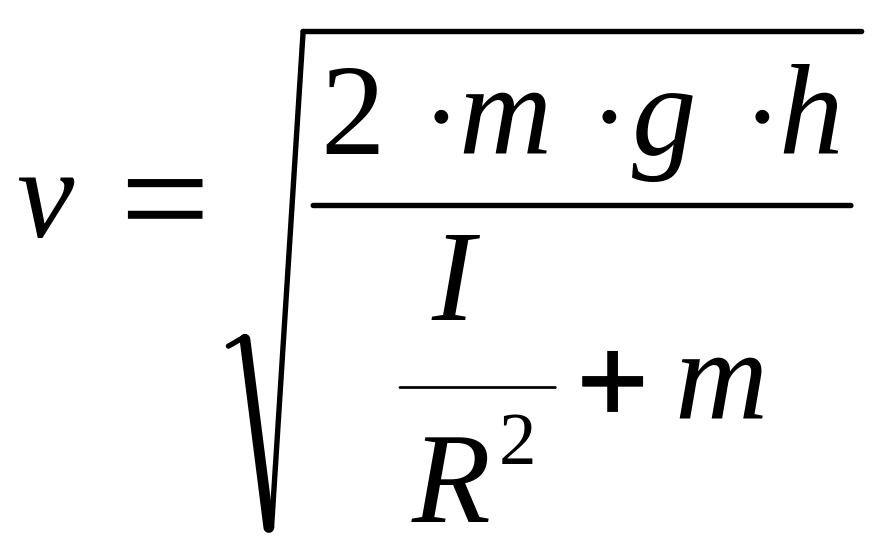(4.9.33)

У загальному випадку, момент інерції тіла сферичної або колової форми радіуса відносно осі обертання, яка проходить через його геометричний центр і є головною віссю інерції, можна записати у вигляді:

(4.9.34)

Так, для однорідної суцільної сфери , а для тонкого кільця .

Ввівши такий коефіцієнт, швидкість, яку набуде тіло з таким коефіцієнтом – характеристикою його моменту інерції буде дорівнювати:

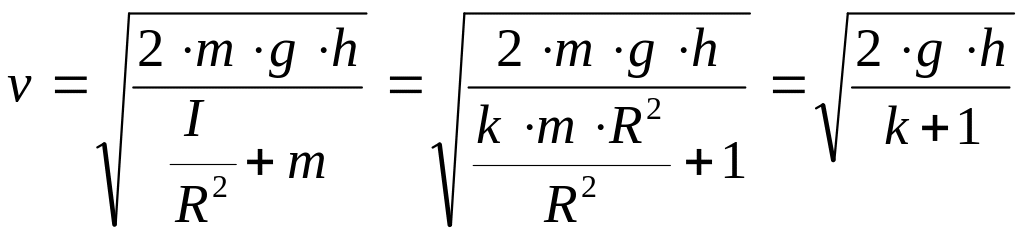(4.9.35)

Тоді шукане відношення двох тіл – суцільної сфери та тонкого кільця буде становити:

. (4.9.36)

4.10. Контрольні питання

1. Який принцип визначення кінетичної енергії обертального руху твердого тіла?

2. Як вводиться поняття моменту інерції твердого тіла, розглядаючи кінетичну енергію його обертового руху?

3. Яка аналогія між формулами кінетичної енергії поступального та обертального рухів твердого тіла?

4. Як записується і формулюється основне рівняння динаміки обертального руху твердого тіла відносно нерухомої осі обертання?

5. Який фізичний зміст моменту інерції тіла?

6. Що собою являє момент сили як скалярна величина?

7. Як визначається вектор моменту сили відносно точки?

8. Як записується основне рівняння динаміки обертального руху у векторній формі?

9. Як вводиться поняття моменту імпульсу тіла і за якою формулою він визначається?

10. Як формулюється і записується закон збереження моменту імпульсу для замкнутої системи?

11. З якими властивостями простору пов'язаний закон збереження моменту імпульсу?

12. Які приклади закону збереження моменту імпульсу?

13. За яким принципом можна математично розрахувати момент інерції різних тіл?

14. Який момент інерції окремих тіл (тонке кільце, суцільний диск, сфера)?

15. Як визначити момент інерції тіла за допомогою теореми Штейнера?

16. Що собою являють вільні осі обертання тіла, головні осі інерції тіла та головні моменти інерції тіла?

17. Як вводиться поняття тензора моменту інерції тіла?

18. В чому полягає гіроскопічний ефект?

19. В чому полягає явище прецесії гіроскопу і як визначити кутову швидкість прецесії гіроскопу?

20. Яке практичне застосування гіроскопів та гіроскопічних ефектів?

5 МЕХАНІКА РІДИН І ГАЗІВ

5.1 Кінематика рідин і газів

Задачею кінематики рідин і газів є вивчення їх руху, не з’ясовуючи причин цього руху. З точки зору механіки рідини і гази є суцільними середовищами. Частинки рідини або газу рухаються одна відносно одної, що робить специфічним опис кінематики рідин і газів. Можливі два способи опису руху рідин і газів. Перший спосіб, який запропонував французький математик Лагранж, полягає в тому, що для кожної точки рідини чи газу у даний момент часу вказується її положення у просторі та швидкість. Уявіть, що в повітря, коли дує вітер, ми запустили величезну кількість повітряних кульок і визначаємо положення та швидкість кожної кульки. У принципі, такий спосіб опису руху рідини чи газу можливий, але практично важко здійснений. Значно простіше слідкувати не за частиками рідини або газу, а за окремими точками простору і фіксувати швидкість, з якою проходять цю точку частики рідини чи газу. Такий спосіб запропонував німецький фізик і математик Ейлер. При цьому способі рух рідини або газу визначається сукупністю функцій для всіх точок простору. Таким чином, сукупність векторів , заданих для кожної точки простору утворюють векторне поле швидкостей. Якщо вектор швидкості в кожній точці простору з часом не змінюється, то така течія називається стаціонарною і, відповідно, векторне поле швидкостей теж буде стаціонарним. Елементи теорії векторного поля на прикладі гравітаційного поля були розглянуті у розділі 2.4.2. Математичний опис як гравітаційного, так і векторного поля швидкостей має багато спільного. Використовується такі ж самі поняття як лінії векторного поля, потоку вектора, дивергенції вектора. Тільки якщо для гравітаційного поля ми говоримо про лінії напруженості або силові, то для векторного поля швидкостей теж використовується аналогічне поняття. Тільки тепер замість ліній напруженості будемо говорити про лінії течії як такі лінії, дотичні до яких у кожній точці визначають напрям швидкості рідини чи газу саме у даній точці.

Таким чином, векторне поле швидкостей можна наглядно зобразити з допомогою ліній течії, як це вказано на рис.5.1.1. Лінію течії можна провести через будь яку точку простору. Якщо провести скільки завгодно ліній, то вони просто зіллються одна з одною. Тому для наглядного зображення течії рідини чи газу будують лише частину ліній, так що по густоті ліній течії можна визначити швидкість рідини або газу. Найпростіший випадок – однорідне векторне поле швидкостей, де лінії течії є паралельні прямі з однаковою густиною. Даючи означення математичного векторного поля абстрактного вектора (див.2.4.2) було сказано, «а чи не нагадують такі паралельні лініє та ще й з стрілочками лінії течії рідини»? Тому тепер замість абстрактного вектора вкажемо на вектор швидкості частинок рідини, яка у буквальному розумінні тече через контур площею . І тепер, знову ж таки, замість абстрактного математичного потоку вектора через контур площею маємо справжній потік рідини, де потік вектора швидкості через площу такого контуру дорівнює

, (5.1.1)

– кут між вектором швидкості та перпендикуляром до поверхні або

, (5.1.2)

де – нормальна проекція площі контуру на напрям вектора швидкості. Потік вектора є скалярна величина і в теорії векторного поля було показано, що потік абстрактного математичного вектора через поверхню визначається скалярним добутком цього вектора на «особливий» вектор площі , де – одиничний вектор, перпендикулярний до даної поверхні. Тому потік вектора швидкості через контур площею як скалярний добуток двох векторів та має наступний вигляд

, (5.1.3)

(порівняйте з…)

Якщо поле вектора швидкості неоднорідне, то загальний потік цього вектора через контур площею дорівнює інтегральній сумі елементарних потоків через елементарні поверхні , у межах яких швидкість можна вважати однаковою

, (5.1.4)

(порівняйте з…)

Що стосується фізичного змісту потоку вектора швидкості, то цей зміст розриває одиниця вимірювання цього потоку

. (5.1.5)

Тобто, потік вектора швидкості через поверхню визначає об’єм рідини, що протікає через дану поверхню за одиницю часу (поверхня орієнтована перпендикулярно до вектора швидкості і поле вектора швидкості однорідне). Якщо вибрати поверхню одиничної площі, що перпендикулярна до вектора швидкості рідини чи газу, то у випадку однорідного векторного поля швидкості потік вектора швидкості через таку поверхню чисельно дорівнює кількості ліній течії, які перетинають цю поверхню. Наприклад, через площу за одну секунду протікає води. Тоді цю площу перетинають 4 перпендикулярні до такої площі лініЇ течії. А якщо об’ємна витрата води , то як через площу провести 0,4 лінії? Дуже просто: площу перпендикулярно до неї перетинає всього одна лінія течії.

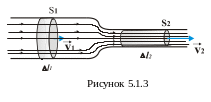Частина рідини або газу, обмежену лініями течії, називається трубкою течії. Приклад трубки течії наведений на рис 5.3, де рідина буквально тече в трубі з різними поперечними перерізами. Рідина практично нестискувана, тому за однаковий час через різні перерізи трубки течії протікають однакові об’єми рідини. За однаковий час частинки рідини у широкій частині трубки течії, маючи швидкість , пройдуть відстань , а у вузькій при швидкості – відстань . Враховуючи рівність об’ємів рідини, які за однаковий час протікають через різні поперечні перерізи трубки течії отримаємо:

. (5.1.6)

Подібні розрахунки стовно до будь якої пари перерізів трубки течії дадуть такий самий результат. Таким чином, для нестискуваної рідини величина у будь-якому поперечному перерізі одної і тієї ж трубки течії повинна бути однаковою

. (5.1.7)

Отриманий результат математично встановлює зміст умови нерозривності струмини, тобто за однакові проміжки часу через будь-які поперечні перерізи трубки течі її протікають однакові об’єми рідини.

Дійсно, добуток визначає потік вектора швидкості, одиницею вимірювання якого є і тому потік вектора швидкості в гідромеханіці називають об’ємною витратою рідини і позначають .

З умови нерозривності струмини впливає, що при зменшенні поперечного перерізу трубки струмини рідини її швидкість збільшується, отже частинки рідини набувають прискорення. Причини такого прискорення встановлює динаміка рідин і газів. Для ідеальних рідин та газів основним рівнянням їх динаміки є рівняння Бернуллі.