1.1.3 Рівномірний рух. Швидкість рівномірного руху

Ми інколи звикаємо до деяких понять, які нам здаються зрозумілими і очевидними. Наприклад, говорячи про рівномірний рух, ми розуміємо, що це рух зі сталою швидкістю. Наприклад, за кожну секунду тіло проходить 10 м. Чи буде такий рух рівномірним? А якщо протягом 0,3 с тіло рухалось повільно, а потім 0,7 с швидко і загалом за 1 с пройшло шлях 10 м, то чи буде такий рух рівномірним? Добре, нехай за кожну 0,1 с шлях становить 1 м, то чи буде такий рух рівномірним? Адже не виключено, що протягом 0,2 с рух повільний, а за наступні 0,8 с, більш швидкий, і т.д., тобто переходимо до часу 0,01 і т.д. Таким чином, якщо за будь-які рівні проміжки часу, якими б вони не були малими, тіло проходить однакові відрізки шляху, то такий рух називаємо рівномірним і для такого руху відношення шляху до часу, за який цей шлях пройдено, є величина стала і це відношення називається швидкістю рівномірного руху (точніше модуль швидкості).

. (1.1.5)

Отже, рівняння кінематики рівномірного руху при природному способі опису руху запишеться:

(1.1.6)

або

, (1.1.7)

де – відстань від початку відліку в момент часу .

Ще раз підкреслимо, що ці рівняння „працюють” тільки тоді, коли відома траєкторія руху. Наприклад, тіло рухається з швидкістю 10 м/с і за час 10 с пройшло шлях 100 м. В якому напрямі рухалось тіло? Для цього треба знати траєкторію руху. Напрям руху автоматично випливає з векторного способу опису цього руху – в якому напрямі вектор переміщення – в такому ж напрямі і рух. Швидкість є векторною величиною і для рівномірного руху вектор швидкості – фізична величина, яка пропорційна вектору переміщення і обернено пропорційна тому часу, за який відбулось це переміщення

. (1.1.8)

Ввівши таким чином поняття вектора швидкості, приходимо до важливого висновку – рівномірним рухом може бути тільки прямолінійний рух, коли швидкість не змінюється не тільки за величиною, але і за напрямом.

Щоб розрізнити швидкість як вектор, і швидкість як скалярну величину в англійській мові існують два терміни “speed” та “velocity” Перший термін стосується тільки числового значення швидкості, (згадаємо спідометр в машині, який не вказує напрям руху автомобіля, а тільки числове значення швидкості). Другий термін стосується вже напряму швидкості, як векторної величини. В українській мові теж була спроба ввести два терміни, але ці терміни не прижились.

1.1.4 Нерівномірний рух. Середня швидкість. Миттєва швидкість

Якщо за рівні проміжки часу тіло проходить не однакові відрізки шляху , то такий рух називається нерівномірний і відношення

(1.1.9)

визначає середню швидкість.

Чим менший час , тим менше нерівномірний рух відрізняється від рівномірного, і лише в границі, коли , рух можна вважати рівномірним. Отже, миттєва швидкість буде математично визначатись як межа, до якої прямує середня швидкість при і як відомо ця границя дає першу похідну від шляху по часу

(1.1.10)

Таким чином, якщо рух матеріальної точки задається відповідною математичною функцією залежності шляху від часу, то миттєва швидкість в будь який момент часу визначається похідною від шляху по часу.

Якщо ж визначати миттєву швидкість як вектор, то маємо аналогічний математичний запис, де замість беремо вектор

(1.1.11)

Тобто, вектор миттєвої швидкості визначається як перша похідна радіуса-вектора по часу.

В вівши поняття вектора миттєвої швидкості, легко показати, що при криволінійному русі цей вектор є дотичний до траєкторії.

Дійсно, розглянемо рис.1.1.6, де вказані переміщення за різні проміжки часу, які послідовно зменшуються.

Чим менший проміжок часу , тим менше переміщення , тобто , і все більше середня швидкість , яка співпадає з , яка і є хордою дуги, наближається до самої дуги. І лише в границі, коли , маємо нескінченно мале переміщення , яке співпадає з дугою і дотичною, отже, вектор миттєвої швидкості є дотичний до траєкторії.

Всі вище наведені приклади стосуються знаходження миттєвої швидкості за заданою функцією шляху від часу , або вектора переміщення від часу .

Тепер розглянемо важливу зворотну задачу – відома залежність швидкості від часу, необхідно визначити шлях, пройдений тілом за цей час.

Нехай залежність швидкості від часу задана деякою функцією , графік якої наведений на рис.1.1.7.

Т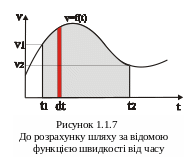 ак як швидкість змінюється, то спочатку визначимо шлях , який пройде тіло за час , протягом якого рух можна вважати рівномірним.

Згідно 1.10 цей елементарний відрізок шляху дорівнює

. (1.1.12)

Легко бачити, що такий шлях чисельно дорівнює площі заштрихованої смужки. Весь шлях буде рівний інтегральній сумі

. (1.1.13)

Ця інтегральна сума чисельно дорівнює сумі площ таких елементарних смужок, тобто в загальному площі криволінійної фігури.