4 Рух тіла, кинутого під кутом до горизонту

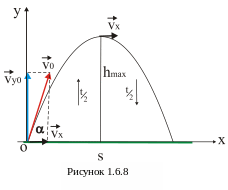Рух тіла, кинутого під кутом до горизонту можна уявити як два незалежних рухи. Так, якщо швидкість v _{0 ,} з якою кинули тіло під кутом α до горизонту, розкласти на дві складові: горизонтальну та вертикальну , як вказано на рис 1.6.8, то тіло здійснює два наступні незалежні рухи:

1. Рівномірний прямолінійний в горизонтальному напрямі з швидкістю v _x

2. Рух тіла, кинутого вертикально вгору з швидкістю v_y0 – до верхньої точки рівносповільнений, а з верхньої точки вниз – рівноприскорений.

Тому задача першого рівня складності про рух тіла, кинутого під кутом горизонту має наступний зміст:

1. Тіло, кинуте зі швидкістю v₀ під кутом α до горизонту. Визначити максимальну висоту підняття тіла, час руху та дальність польоту тіла (відстань по горизонталі від точки кидання до точки падіння).

Тепер математично опишемо ці рухи:

1. Рівняння рівномірного руху

,

де S – дальність польоту тіла, відстань по горизонталі від точки кидання до точки падіння за час t.

Позначивши час всього руху t, час руху вгору до верхньої точки буде становити t/2 (такий самий час руху вниз). Використовуючи відомі співвідношення для вільного падіння, можна записати наступні рівняння, де h – максимальна висота підняття.

.

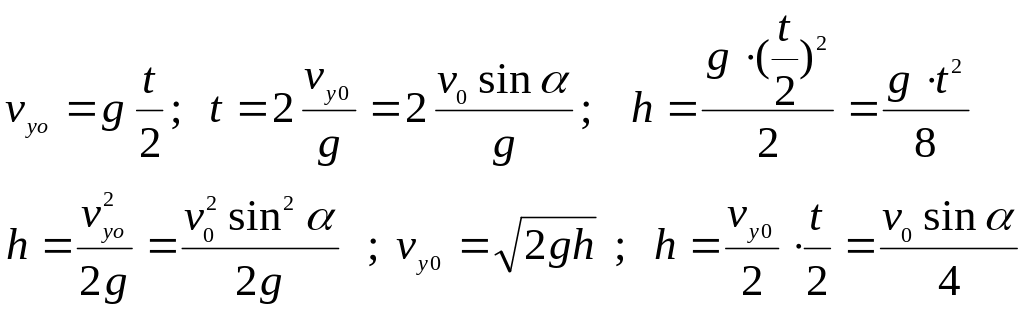
Використовуючи ці формули, легко розв’язати задачі першого рівня складності, де треба з цих формул визначити ту чи іншу величину. До другого рівня складності можна віднести задачі про визначення радіуса кривизни траєкторії у верхній точці та швидкості тіла у будь якій точці траєкторії. Тому на цих задачах доцільно зупинитись біль детально.

2. Тіло, кинуте під кутом до горизонту з швидкістю v_0. Визначити радіус r кривизни траєкторії у її верхній точці.

Типова помилка, яку допускають при розв’язку даної задачі полягає в тому, що радіусом кривизни траєкторії вважають максимальну висоту підняття тіла. Але зверніть увагу на рисунок – верхня частина траєкторії являє собою вершину параболи. В принципі, виключивши час з рівнянь руху по горизонталі та по вертикалі (вісь У), можна отримати рівняння траєкторії і з цього рівняння можна визначити радіус кривизни кривої (параболи) в будь-якій точці. Але фізика дає простий розв’язок поставленої задачі. Ще раз зверніть увагу на точку у верхній частині траєкторії. У цій точці вектор прискорення вільного падіння перпендикулярний до вектора швидкості , отже прискорення вільного падіння у верхній точці траєкторії виконує роль нормального (доцентрового) прискорення. Тому

.

В окремих випадках розв’язування навіть складних задач кінематики спрощується застосуванням закону збереження і перетворення енергії. Це стосується кінематики руху тіла, кинутого вертикально, горизонтально або під кутом до горизонту. Наприклад:

3. Тіло, кинуте під кутом до горизонту з швидкістю v_{0 .} Визначити швидкість тіла на довільній висоті у .

В умові задачі не вказаний кут кидання, тому, як кажуть в приказці, «обійдемо всі гострі кути», і за що тут можна «зачепитися» без кута, який не вказаний в умові. Є одна непогана ідея – невідома швидкість та відома є гіпотенузами прямокутних трикутників, в яких є однаковий катет v_x, а другий катет – швидкість у вертикальному напрямі, і ця швидкість зменшується з висотою. Отже, необхідно записати такі рівняння

Так як (див. таблицю формул на ст….), то, відповідно, .

Тепер ця сама задача з точки зору збереження і перетворення енергії. А саме: якщо б тіло досягло максимальної висоти, то кінетична енергія тіла повістю перейшла би в потенціальну енергію. Але тут тіло не на максимальній висоті, воно володіє як кінетичною, так і потенціальною енергією, тому, згідно закону збереження та перетворення енергії, будемо мати

.

Переконались – як просто без геометрії та формул кінематики знайдена шукана кінематична величина. Забігаючи наперед, відмітимо – застосування закону збереження і перетворення енергії є надзвичайно потужним методом опису процесів різної природи. В розділі «ДИНАМІКА» ми покажемо, що замість диференціального рівняння, яке описує зісковзування шнура зі столу досить застосувати елементарну формулу перетворення потенціальної енергії в кінетичну. Але щоб не склалось враження про можливість розв’язку таким способом абсолютно всіх задач, перейдемо до задачі третього рівня про рух тіла, кинутого під кутом до горизонту з нестандартними умовами, які вимагають теж нестандартного підходу до їх розв’язку. Тут не можна дати готових вказівок – застосування тієї чи іншої формули.

4. Із шланга, який лежить на землі, під кутом б’є вода з початковою швидкістю 10 м/с. Площа перерізу отвору S=5 см². Визначити масу струменя води, яка перебуває в повітрі. Густина води 1000 кг/м³.

Якщо б ми знали об’єм V струминю води, що знаходиться в повітрі, то маса цієї води дорівнювала би . Питання – як знайти такий об’єм. В принципі, склавши рівняння траєкторії (це буде парабола з вершиною в найвищій точці), математично означеним інтегралом можна знайти її довжину. Але ми спробуємо, якщо нам вдасться, обійтись без вищої математики, добре подумавши – а звідкіля береться цей струмінь води? Для цього згадаємо дитячий водяний пістолет, який вистрілює струмінь води, тобто об’єм води, що був в пістолеті опиняється в повітрі. Так ось, роль такого вже не водяного пістолета, а, по суті, водяної гармати, буде виконувати шланг-труба, в якій переміщається зі швидкістю v поршень площею S. З цієї труби, нахиленої під кутом α до горизонту, б’є вода з такою ж швидкістю, з якою рухається поршень. Шланг, тобто труба, заповнені водою, струмінь поки що відсутній, пунктиром позначена майбутня траєкторія (рис 1.6.11 А). Далі при русі поршня траєкторія руху все більше заповнюється водою і коли запаси води в трубі закінчаться, як вказано на другій позиції рисунку 1.6.11Б, вода буде в повітрі.

Отже, шуканий об’єм води дорівнює , де L – переміщення поршня, так що . А час t руху поршня і буде часом руху тіла, кинутого під кутом до горизонту, де в даному випадку таким тілом є струмінь води. Цей час, як вже було раніше вказано, дорівнює

.

Тому шукана маса води буде становити

,

а підставивши числові значення всіх величин отримаємо, що m=7,2 кг.

Розглянуті задачі про рух тіла, кинутого під кутом до горизонту стосувались того випадку, коли точка кидання та падіння знаходяться на одній горизонтальній прямій. Але можуть бути інші випадки. Тіло кидають з деякої висоти під кутом до горизонту вгору або вниз. Тому окремо розглянемо такі випадки.

5. Спортсменка штовхає ядро з висоти свого обличчя на висоті 165 см під кутом 45⁰ з швидкістю 12 м/с. Визначити дальність польоту ядра (відстань по горизонталі від точки кидання до точки падіння ( хоча в спорті цю відстань відраховують від краю сектора для штовхання ядра).

.

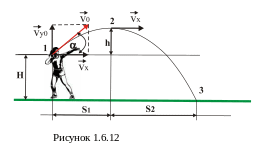
9. Тут зручно рух ядра розділити на дві частини (рис.1.6.12): 1) рух тіла, кинутого під кутом до горизонту, але рух лише до верхньої точки протягом часу t₁ і тіло ще піднімається на «додаткову» висоту h). 2) Рух тіла, кинутого горизонтально з висоти H+h і цей рух буде тривати час t₂ до падіння ядра на землю.

Визначивши принцип (ідею) розв’язку задачі справа лишається за технікою – скласти рівняння вказаних рухів.

1. Рух від точки 1 до 2.

.

2. Рух від точки 2 до 3.

.

Тоді дальність польоту становитиме

.

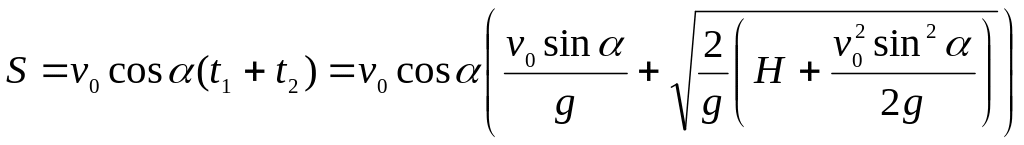Підставивши числові значення, отримаємо S=15,86 м. Найвищий результат по штовханню ядра серед жінок був встановлений у 2010 Надією Остапчук. Вона штовхнула ядро на 20,85м на зимовому чемпіонаті світу.

З деякої висоти (балкона, вежі, з крутого берега ріки і т.п.) тіло можуть кидати під кутом до горизонту тільки не вгору, а вниз. Тому прикладом такого руху тіла, кинутого з висоти вниз зі швидкістю під кутом до горизонту буде наступна задача.

6. З літака, який летить на висоті 500 м з швидкістю 360 км/год під кутом 20⁰ до горизонту скидають вантаж. На якій відстані по горизонталі від точки падіння вантаж впаде на землю, якщо опором повітря знехтувати?

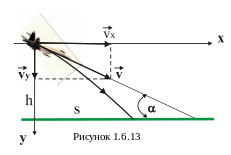5. Якщо розкласти швидкість v на дві складові: v_x - горизонтальну та v_y -вертикальну (рис.1.6.13), то вантаж приймає участь в двох незалежних рухах

1. Рівномірний прямолінійний в горизонтальному напрямі з швидкістю v_x

_.

2. Рух тіла, кинутого вертикально вниз з висоти h з початковою швидкістю

.

Підставивши числові значення і розв’язавши таке квадратне рівняння, отримаємо: час руху становитиме t=7,2 c. Тоді, згідно першого рівняння, шукана відстань S буде мати наступне значення

.