
- •6.040103 – «Геологія»
- •1 Кінематика
- •1.1 Кінематика матеріальної точки
- •Система відліку
- •1.1.2 Матеріальна точка. Способи опису руху матеріальної точки
- •1.1.3 Рівномірний рух. Швидкість рівномірного руху
- •1.1.4 Нерівномірний рух. Середня швидкість. Миттєва швидкість
- •1.1.5 Рівнозміний рух. Прискорення. Змінний рух. Миттєве прискорення
- •1.1.6 Прискорення при криволінійному русі. Нормальне і тангенціальне прискорення
- •Абсолютно тверде тіло та число ступенів його свободи
- •1.3 Кінематика обертального руху твердого тіла
- •1.3.1 Обертальний рух твердого тіла відносно нерухомої вісі обертання. Вектор кутового переміщення. Кутова швидкість. Кутове прискорення.
- •1.3.2. Зв'язок між кутовими і лінійними кінематичними величинами обертального руху
- •1.4 Кінематика відносного руху. Переносне прискорення. Прискорення каріоліса
- •1. Чим більша відстань від центра обертання, тим більша лінійна швидкість обертання. Тобто, маємо зміну швидкості, викликану лише переміщенням точок .
- •1.5 Короткий зміст основних питань кінематики
- •4. Способи опису руху матеріальної точки:
- •6. Миттєва швидкість
- •7. Рівнозмінний рух. Прискорення.
- •8. Змінний рух. Середнє прискорення. Миттєве прискорення.
- •9. Прискорення при криволінійному русі. Нормальне і тангенціальне прискорення.
- •10. Поступальний рух тіла.
- •11. Обертальний рух тіла.
- •16. Кутове прискорення.
- •17. Зв'язок між лінійними і кутовими кінематичними величинами обертового руху.
- •3. Одна пряма рухається паралельно сама собі з швидкістю v1, а друга – зі швидкістю v2.. Питання: з якою швидкістю v3 рухається точка перетину цих прямих?
- •2.Задачі на рівно змінний рух
- •1. Автомобіль проходить гальмівний шлях 20 м. Визначити час руху автомобіля до зупинки та модуль прискорення, якщо початкова швидкість 54 км/.
- •3. Град, падаючи з хмари за останню секунду свого падіння пролітає шлях, що становить 0,19 всієї висоти. Визначити час падіння та висоту, з якає падає град. Опором повітря нехтувати.
- •3 Рух тіла, кинутого горизонтально
- •4 Рух тіла, кинутого під кутом до горизонту
- •5.Задачі на середню і миттєву швидкість та миттєве прискорення
- •2. Першу половину часу автомобіль рухався з швидкістю 60 км/год, а другу половину часу з швидкістю 40 км/год. Визначити середню швидкість протягом всього часу.
- •3. Першу половину шляху автомобіль рухався з швидкістю 60 км/год, а другу половину шляху з швидкістю 40 км/год. Визначити середню швидкість протягом всього часу.
- •6.Задачі кінематики обертального руху
- •1. Колесо починає обертатись зі стану спокою і, зробивши 100 обертів, досягає кутової швидкості 62,8 рад/с. Вважаючи рух рівноприскореним, визначити час та кутове прискорення даного обертового руху.
- •4. У вибраній системі відліку з декартовими координатами кінематичні рівняння матеріальної точки мають наступний вигляд:
- •5. Задача-тест.
- •1.7 Контрольні питання з кінематики
- •2 Динаміка матеріальної точки (тіла) при поступальному русі. Закони ньютона. Сили в механіці. Гравітація
- •2.1 Динаміка матеріальної точки (тіла) при поступальному русі. Закони Ньютона
- •2.2 Сили в природі. Сили в механіці
- •2.2.1 Сили тертя
- •2.2.2 Сили пружності
- •2.3 Гравітація
- •2.3.1 Закони Кеплера. Закон Всесвітнього тяжіння
- •3. Квадрати періодів обертання планет навколо Сонця відносяться як куби великих піввісей їх орбіт:
- •2.3.2 Експериментальне визначення гравітаційної сталої. Дослід Кавендиша
- •2.3.3 Гравітаційна взаємодія тіл довільної форми
- •4 Гравітаційне поле. Напруженість гравітаційного поля
- •5 Елементи теорії векторного поля. Теорема Остроградського-Гауса
- •6 Гравітаційне поле Землі (поле тіла сферичної форми)
- •7 Аномалії гравітаційного поля Землі. Поняття про гравітаційну
- •2.4 Рух тіл в полі тяжіння. Вага тіла. Невагомість. Штучні супутники
- •2.4.1 Вага тіла
- •2.4.2 Рух тіла у полі тяжіння у вертикальному напрямі. Перевантаження. Невагомість
- •2.4.3 Криволінійний рух тіла у полі тяжіння
- •2.4. 4 Вплив обертання Землі на вагу тіл
- •1 Тіло на полюсі
- •2 Тіло на екваторі
- •3 Тіло на довільній широті
- •5 Штучні супутники Землі
- •2.6 Короткий зміст основних питань динаміки
- •3. Сили в природі. Сили в механіці.
- •4. Сили тертя.
- •5. Сили пружності.
- •6. Закони Кеплера.
- •Планети рухаються по еліпсах, в одному з фокусів яких знаходиться Сонце (рис.2.4.2).
- •7. Закон Всесвітнього тяжіння
- •8. Експериментальне визначення гравітаційної сталої. Дослід Кавендиша.
- •9. Гравітаційна взаємодія тіл довільної форми
- •10. Гравітаційне поле
- •10. Вага тіла
- •1. Потік вектора
- •2.7 Приклади розвязування задач
- •1. Рух тіла в горизонтальному напрямі під дією декількох сил
- •2. Дано:
- •5. Рух тіла під дією змінної сили.
- •6. Рух тіла по похилій площині
- •7. Динаміка руху тіла по колу
- •Випадок руху тіла по колу у вертикальній площині – рух тіла на нитці.
- •10. Який період обертання у горизонтальній площині тіла, підвішеного на нитці довжиною l, якщо нитка утворює з вертикаллю кут α?
- •8. Закон всесвітнього тяжіння. Гравітаційне поле
- •1 Визначити силу притягання між тонким кільцем радіуса r і масою м та матеріальною точкою масою m, яка знаходиться на відстані l від центра кільця.
- •2. Матеріальна точка масою m знаходиться на віддалі a від нескінченно довгої тонкої нитки з лінійною густиною . Визначити силу, з якою притягаються така нитка і тіло точкової маси.
- •2.7 Контрольні питання з динаміки
- •3. Закони збереження в механіці
- •3.1 Закон збереження імпульсу
- •3.2 Центр мас. Теорема про рух центра мас
- •3.3 Реактивний рух
- •3.4 Реактивний рух в природі. Живі ракети
- •3.5 Робота сталої і змінної сил. Потужність
- •3.6 Енергія. Загальний підхід до поняття енергії
- •3.7 Кінетична енергія матеріальної точки (тіла) при поступальному русі
- •3.8 Робота сил тяжіння. Потенціальна енергія тіла в полі тяжіння
- •3.9 Закон збереження енергії в механіці
- •3.10 Застосування законів збереження до співудару двох тіл
- •3.11 Основні напрями альтернативної енергетики
- •1. Вітроенергетика
- •2. Геліоенергетика
- •3. Геотермальна енергетика
- •1. Вітроенергетика
- •2. Альтернативна гідроенергетика
- •3.12 Короткий зміст основних питань законів збереження в механіці
- •1. Закон збереження імпульсу
- •2. Центр мас. Теорема про рух центра мас
- •3. Реактивний рух
- •4. Робота сталої і змінної сил. Потужність
- •5. Енергія. Кінетична і потенціальна енергія
- •6. Закон збереження енергії в механіці.
- •3.13 Приклади розв’язування задач
- •1. Імпульс. Закон збереження імпульсу
- •1. М’ячик масою 200 г вільно падає з висоти 5м на горизонтальну поверхню. Вважаючи удар абсолютно пружним, визначити зміну імпульсу при такому ударі (рис.3.13.1).
- •3. Два тіла рухаються назустріч одне одному з швидкостями . Після абсолютно непружного удару ці тіла стали рухатись разом з швидкістю . Визначити відношення мас цих тіл.
- •4. З самохідної гарматної установки загальною масою 8 т вистрілюють снаряд масою 5 кг зі швидкістю 1200 м∕ с під кутом 600 до горизонту. Визначити швидкість віддачі установки.
- •3.14 Контрольні питання
- •4 Динаміка обертального руху твердого тіла відносно нерухомої осі обертання
- •4.1 Кінетична енергія обертального руху твердого тіла відносно нерухомої осі обертання. Момент інерції тіла
- •4.2 Основне рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання
- •4.3 Момент імпульсу. Закон збереження моменту імпульсу
- •4.4 Моменти інерції різних тіл. Теорема Штейнера
- •3. Момент інерції однорідного диска або циліндра
- •4. Момент інерції конуса
- •5. Момент інерції однорідної суцільної кулі
- •6. Момент інерції тонкостінної сфери
- •4.5 Вільні осі обертання тіла. Головні осі інерції тіла. Головні моменти інерції тіла. Поняття про тензор моменту інерції тіла
- •4.6 Гіроскопічний ефект. Прецесія гіроскопа
- •4.7 Застосування гіроскопів та гіроскопічних ефектів
- •4.8 Короткий зміст основних питань динаміки обертового руху твердого тіла
- •Кінетична енергія обертового руху твердого тіла відносно нерухомої осі обертання. Момент інерції тіла
- •Основне рівняння динаміки обертового руху твердого тіла
- •3. Момент імпульсу. Закон збереження моменту імпульсу
- •4. Моменти інерції різних тіл. Теорема Штейнера
- •5. Вільні осі обертання тіла. Головні осі інерції тіла. Головні моменти інерції тіла. Поняття про тензор моменту інерції тіла
- •Гіроскопічний ефект. Прецесія гіроскопа
- •Застосування гіроскопів та гіроскопічних ефектів
- •4.9 Приклади розв’язування задач
- •2. Перевірка основного рівняння динаміки обертового руху твердого тіла відносно нерухомої осі обертання.
- •5.2 Рівняння Бернуллі
- •5.3 Наслідки з рівняння Бернуллі
- •5.3.1 Швидкість витікання рідини через невеликий отвір
- •5.3.2 Горизонтально розташована трубка течії. Вимірювання швидкості течії
- •5.3.3 Застосування наслідків з рівняння Бернуллі в техніці
- •5.4 Внутрішнє тертя в рідинах і газах (в’язкість)
- •5.5 Течія Пуазейля. Формула Пуазейля
- •5.6 Ламінарний та турбулентний режим течії. Числа Рейнольда. Рух тіл в рідинах і газах
- •5.7 Елементи реології
- •1. Ньютонівські та неньютонівські системи
- •2 Експериментальні методи вивчення в’язкості
- •2. Ротаційні віскозиметри
- •3 Метод Стокса
- •5.8 Короткий зміст основних питань механіки рідин і газів
- •8. Наслідки з рівняння Бернуллі.
- •2. Горизонтально розташована трубка течії. Вимірювання швидкості течії.
- •3. Застосування наслідків з рівняння Бернуллі в техніці.
- •4. Природні явища, де мають місце наслідки з рівняння Бернуллі.
- •9. Внутрішнє тертя в рідинах і газах (в’язкість).
- •10. Течія Пуазейля. Формула Пуазейля.
- •11. Ламінарний та турбулентний режим течії. Числа Рейнольда. Рух тіл в рідинах і газах
- •12. Елементи реології.
- •1. Ньютонівські та неньютонівські системи.
- •Експериментальні методи вивчення в’язкості
- •1. Капілярні віскозиметри
- •2. Ротаційні віскозиметри
- •3. Метод Стокса
- •5.9 Приклади розв’язування задач
- •1. Швидкість течії води у широкій частині труби дорівнює 20 см ∕с. Яка швидкість течії у вузькій частині, що має діаметр у 4 рази менший від діаметра широкої частини?
- •2 . З отвору площею поперечного перерізу зі швидкістю у вертикальному напрямі витікає струмина рідин. Якою буде площа поперечного перерізу струмини на висоті ?
- •6 Механічні властивості твердих тіл
- •6.1 Основні види пружних деформацій твердого тіла
- •1. Одностороння деформація розтягу (стиснення).
- •2. Деформація зсуву.
- •3. Деформація кручення.
- •4. Деформація прогину.
- •5. Деформація стиснення (або розтягу).
- •6.2 Твердість тіл
6 Механічні властивості твердих тіл
У попередньому розділі механіки рідин і газів розглядалась механіка суцільних середовищ, де у кожній точці простору присутня речовина. Що стосується механічних властивостей твердих тіл, то найбільш загальні властивості їх деформацій теж можна розглядати як деформацію суцільних середовищ. Тобто, встановлюючи найбільш загальні характеристики деформації тіла, не обов’язково звертатись до його внутрішньої будови. Дійсно, розглядаючи сили пружності на прикладі деформації пружини, ми встановлювали залежність деформації (видовження пружини) від прикладеної сили, а не змін відстані між вузлами кристалічної решітки металу, з якого виготовлена дана пружина. Таким чином, вважаючи тверде тіло суцільним середовищем, деформацію такого тіла описати відповідним зміщенням частинок цього тіла одне відносно одного.
6.1 Основні види пружних деформацій твердого тіла
 Найпростіший
закон, що описує односторонню пружну
деформацію тіла під дією прикладеної
до нього сили – це відомий закон Гука.
Ще раз нагадаємо цей закон, який говорить,
що у межах пружності сила пружності
пропорційна зміні лінійних розмірів
тіла (видовженню або стисненню тіла).
Тому розгляд основних видів деформації
почнемо з одностороннього розтягу (або
стиску).
Найпростіший
закон, що описує односторонню пружну
деформацію тіла під дією прикладеної
до нього сили – це відомий закон Гука.
Ще раз нагадаємо цей закон, який говорить,
що у межах пружності сила пружності
пропорційна зміні лінійних розмірів
тіла (видовженню або стисненню тіла).
Тому розгляд основних видів деформації
почнемо з одностороннього розтягу (або
стиску).
1. Одностороння деформація розтягу (стиснення).
Під односторонньою
деформацією розуміють таку деформацію,
коли змінюються лінійні розміри тіла
лише в одному напрямі. Для прикладу
розглянемо тіло у вигляді однорідного
стержня або циліндра (рис.6.1.1). Деформація
(на рисунку це розтяг) відбувається під
дією сили F, яка прикладена перпендикулярно
до поперечного перерізу стержня і під
дією цієї сили довжина стержня змінилась
на
![]() ,
як різниця між кінцевим і початковим
значення його довжини. Звичайно,
абсолютне значення зміни лінійних
розмірів
тіла ще не дає уявлень про механічні
властивості речовини, з якого виготовлене
дане тіло (стержень). Дійсно, нехай
,
як різниця між кінцевим і початковим
значення його довжини. Звичайно,
абсолютне значення зміни лінійних
розмірів
тіла ще не дає уявлень про механічні
властивості речовини, з якого виготовлене
дане тіло (стержень). Дійсно, нехай
![]() ,
це багато чи мало – залежить від значення
початкових розмірів. Тому, описуючи
деформацію тіл, вводять поняття відносної
деформації. У нашому випадку це відношення
абсолютного видовження
до початкової довжини
,
це багато чи мало – залежить від значення
початкових розмірів. Тому, описуючи
деформацію тіл, вводять поняття відносної
деформації. У нашому випадку це відношення
абсолютного видовження
до початкової довжини
![]() :
:
![]() .
(6.1.1)
.
(6.1.1)
Крім того, відносна
зміна лінійних розмірів тіла при одному
і тому ж значенні прикладеної сили
залежить від площі поперечного перерізу
тіла. Не важко переконатись: чим більша
площа поперечного перерізу тіла, тим
для однакового видовження потрібна
більша сила. Тому, математично описуючи
зміну лінійних розмірів тіл під дією
прикладеної сили F, необхідно ще
враховувати площу S поперечного перерізу
цього тіла. Відношення сили F, яка
прикладена до площі S поперечного
перерізу тіла, називається механічне
напруження і позначається
![]() :
:
![]() .
(6.1.2)
.
(6.1.2)
Одиницею механічного
напруження є
![]() .
.
У межах
пружної деформації відносна зміна
лінійних розмірів тіла пропорційна
механічному напруженню
![]() .
Тепер для знаку рівності необхідний
коефіцієнт, який би враховував пружні
механічні властивості речовини даного
тіла і, звичайно, залежав би від вибору
системи одиниць вимірювань. Такий
коефіцієнт ввів англійський фізик Юнг
і назва цього коефіцієнту – модуль
Юнга,
позначається буквою Е
(перша буква
у слові
Expantion
– розширення, розтяг). Ввівши такий
модуль, закон односторонньої пружної
деформації прийме наступний вигляд:
.
Тепер для знаку рівності необхідний
коефіцієнт, який би враховував пружні
механічні властивості речовини даного
тіла і, звичайно, залежав би від вибору
системи одиниць вимірювань. Такий
коефіцієнт ввів англійський фізик Юнг
і назва цього коефіцієнту – модуль
Юнга,
позначається буквою Е
(перша буква
у слові
Expantion
– розширення, розтяг). Ввівши такий
модуль, закон односторонньої пружної
деформації прийме наступний вигляд:
![]() (6.1.3)
(6.1.3)
або
![]() .
(6.1.4)
.
(6.1.4)
З останнього рівняння легко розкрити фізичний зміст модуля Юнга.
Якщо
![]() ,
то
,
то
![]() ,
тобто
,
тобто
модуль Юнга Е для речовини даного тіла дорівнює такому нормальному механічному напруженню , яке зумовлює відносну зміну довжини цього тіла, рівну одиниці.
Якщо
,
то це значить
![]() ,
тобто довжина тіла збільшується у два
рази, таким чином
модуль
Юнга Е для речовини даного тіла дорівнює
такому нормальному механічному
напруженню
,
яке зумовлює його видовження у два рази
(якщо б при такій деформації виконувався
закон Гука).
,
тобто довжина тіла збільшується у два
рази, таким чином
модуль
Юнга Е для речовини даного тіла дорівнює
такому нормальному механічному
напруженню
,
яке зумовлює його видовження у два рази
(якщо б при такій деформації виконувався
закон Гука).
Зрозуміло, що більшість твердих тіл просто не втримають такого механічного напруження, при якому вони розтягуються вдвічі. Тому у таблицях механічних властивостей різних матеріалів, крім модуля Юнга, вказується максимальне механічне напруження або границя міцності, після якого тіло руйнується.


 Визначення
механічних властивостей різних
матеріалів в лабораторних умовах
здійснюється за допомогою спеціальних
установок, які називаються розривними
машинами. Сучасні розривні машини
поєднують потужну механічну частину,
яка розтягує або стискає досліджуваний
матеріал та систему здавачів, що фіксують
механічні навантаження і деформації
досліджуваного взірця. Інформація від
таких здавачів у вигляді електричних
сигналів поступає на комп’ютер розривної
машини і комп’ютер видає отриману
залежність деформації від механічного
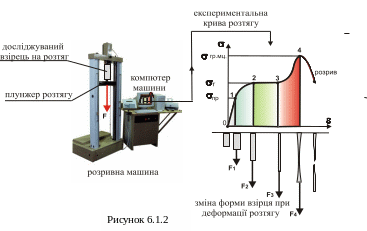
напруження. На рис.6.1.2 наведено загальний
вигляд розривної машини. Досліджуваний
взірець розтягується плунжером (поршнем)
потужного гідравлічного приводу. На
моніторі комп’ютера можна бачити
отриману експериментальну криву розтягу
з наступними характерними ділянками.
Визначення
механічних властивостей різних
матеріалів в лабораторних умовах
здійснюється за допомогою спеціальних
установок, які називаються розривними
машинами. Сучасні розривні машини
поєднують потужну механічну частину,
яка розтягує або стискає досліджуваний
матеріал та систему здавачів, що фіксують
механічні навантаження і деформації
досліджуваного взірця. Інформація від
таких здавачів у вигляді електричних
сигналів поступає на комп’ютер розривної
машини і комп’ютер видає отриману
залежність деформації від механічного
напруження. На рис.6.1.2 наведено загальний
вигляд розривної машини. Досліджуваний
взірець розтягується плунжером (поршнем)
потужного гідравлічного приводу. На
моніторі комп’ютера можна бачити
отриману експериментальну криву розтягу
з наступними характерними ділянками.
0-1. Ця ділянка відповідає малим відносним змінам лінійних розмірів тіла, при яких справджується лінійний закон пружної деформації Гука. Найбільше напруження, до якого ще має місце закон Гука, називається межею пропорційності.
1-2. Подальше збільшення напруження зумовлює нелінійний характер видовження тіла і після припинення дії механічного напруження тіло вже не відновлює попередню форму.
3-4. Ділянка плинності або течії твердого тіла. Без збільшення механічного напруження має місце збільшення деформації тіла, яке веде себе подібно до рідини, тобто «тече» . Якщо прослідкувати за зміною форми тіла, то при такій плинності воно стає тоншим, як це показано на рис.6.1.2.
4-5. При напруженнях, перевищуючих межу текучості, пружні властивості тіла у деякій мірі відновлюються і тіло знову починає чинити опір деформації. Тіло зазнає значних змін форми, утворюється характерне звуження, у якому в подальшому наступає розрив при напруженні, яке визначає границю міцності.
