3.10 Застосування законів збереження до співудару двох тіл

Вище окремо було розглянуто фундаментальні закони збереження – закон збереження імпульсу та закон збереження енергії. На основі цих законів можна пояснити багато явищ і кількісно описати ці явища. Застосування цих законів в окремих випадках значно спрощує розв’язок окремих задач, про що Ви переконались на окремих прикладах з кінематики і динаміки.

Одне з важливих застосувань законів збереження – це співудар двох тіл. А саме, відомі маси тіл та їх швидкості до співудару, необхідно знайти швидкості після їх взаємодії.

Розглянемо два випадки: абсолютно не пружній удар та абсолютно пружній.

До взаємодії імпульс тіл, як замкнутої системи дорівнює:

. (3.10.1)

П ісля напруженої взаємодії тіла рухаються, як єдине ціле масою та з швидкістю і імпульс тіл становить:

, (3.10.2)

тоді, згідно закону збереження імпульсу:

, (3.10.3)

звідки шукана швидкість дорівнює

. (3.10.4)

Для практичних розрахунків співвідношення необхідно спроектувати на вибраний напрям. Згідно рис. 3.10.1, в проекціях на вісь ОХ будемо мати:

. (3.10.5)

При тіла рухаються в напрямі вибраної осі ОХ.

Якщо порівняти кінетичні енергії тіл до удару і після удару, то вони не рівні, частина механічної енергії «щезає», перетворюється у внутрішню енергію при недружній деформації. Визначимо цю різницю енергій:

. (3.10.6)

Т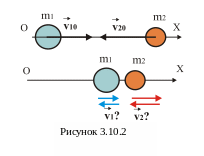 епер розглянемо абсолютно пружній удар, при чому обмежимось центральним ударом двох однорідних куль. Удар називається центральним, якщо кулі до удару рухаються вздовж прямої, яка проходить через їх центри. Відомі маси тіл , та їх швидкості , , до удару. Необхідно визначити швидкості цих тіл після удару (рис.3.10.2).

При такому пружному співударі виконуються закони збереження енергії та імпульсу

(3.10.7)

. (3.10.8)

Опускаючи громіздкий сумісний розв’язок системи цих двох рівнянь (пропонується зробити самостійно), запишемо кінцевий результат, який визначає швидкість кожного тіла після цього абсолютно пружного співудару:

, (3.10.9)

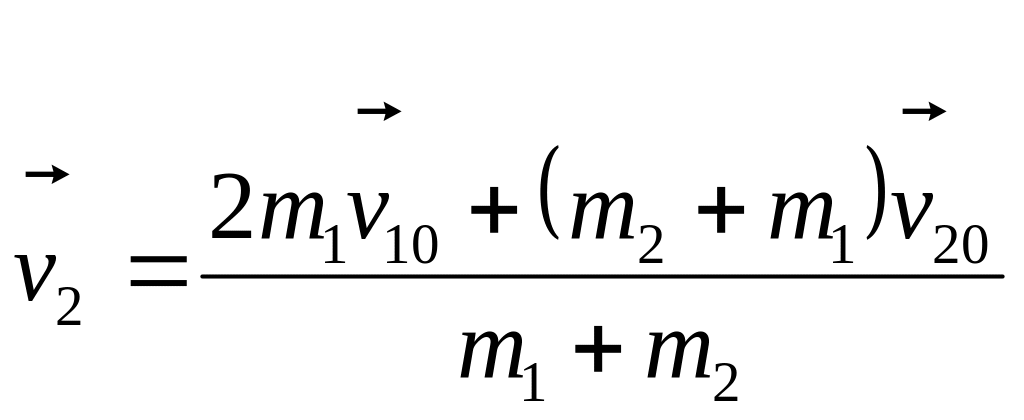. (3.10.10)

Р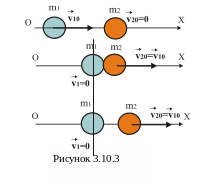 озглянемо окремий випадок, коли маси куль однакові. Тоді при , як випливає з (3.10.9) та (3.10.10), , , тобто кулі при співударі обмінюються швидкостями. Якщо ж друга куля до удару буде нерухома, то після удару вона почне рухатись з швидкістю першої. Приклад такої взаємодії двох кульок однакової маси наведений на рис.3.10.3. Перша кулька вдаряється об нерухому кульку і зупиняється, зате друга кулька починає рухатись з швидкістю першої кульки. Якраз такий випадок центрального пружного удару показаний на рис.3.10.4. при грі в більярд. Гравець ударяє перший шар, надаючи йому швидкості , після чого цей шар, вдаряючись об другий, нерухомий шар, зупиниться. Другий шар, набувши швидкості першого шару, попаде у лузу. Якщо говорити про гру у більярд, то центральний удар шарів найбільш простий елемент гри. Створена ціла науки гри в більярд і, між іншим, відомий фізик і математик Каріоліс іменем якого назване каріолісове прискорення (див. розділ кінематики) написав книжку « Математична теорія явищ більярдної гри».

Розглянутий абсолютно пружний удар – ідеальний випадок. При цьому удар поділяється на дві фази: фазу абсолютно пружної деформації тіла і фазу повного відновлення попередньої форми тіла. У більшості випадків повного відновлення попередньої форми тіл не наступає, що супроводжується втратами кінетичної енергії тіл. Тому для врахування втрат кінетичної енергії при ударах тіл вводять коефіцієнт відновлення, який визначають наступним чином. Так, якщо швидкість першого тіла до удару і ця швидкість при абсолютно пружному ударі входить у всі формули закону збереження енергії та імпульсу, то при реальній, не абсолютно пружній деформації, швидкість зменшиться до і саме ця зменшена швидкість буде визначати результат співудару з іншим тілом. Так само друге тіло не є абсолютно пружним, що приведе до зменшення швидкості з до . Відношення модуля різниці реальних швидкостей двох тіл до модуля різниці швидкостей цих самих, але тільки абсолютно пружних тіл і буде коефіцієнтом відновлення:

. (3.10.11)

Значення коефіцієнта відновлення для різних тіл визначається дослідним шляхом. Наприклад, для дерева , для сталі , для тенісного м’ячика , а для більярдної кульки, виготовленої з слонової кості .

Можна довести що з врахуванням коефіцієнта відновлення модулі швидкостей двох тіл після удару, вказаного на рисунку 3.7.2, будуть мати такі значення:

, (3.10.12)

. (3.10.13)