2. Абсолютно тверде тіло та число ступенів його свободи

Х то з захопленням не спостерігав за фігурами вищого пілотажу, які здійснюють льотчики – аси, де керовані ними сучасні реактивні літаки здійснюють неймовірні повороти, так званні «бочки», піке з переходом на мертву петлю і т.п.

З точки зору кінематики літак являє собою абсолютно тверде діло, яке здійснює складний рух. Нагадаємо, що абсолютно твердим тілом в механіці вважають таким, відстані між будь якими двома точками не змінюється.

Всі попередні розділи стосувались кінематики матеріальної точки, положення якої в просторі визначається трьома координатами. А як визначити положення твердого тіла, яке є системою багатьох точок. Тоді, якщо тіло є системою з 1000 або більше точок то чи треба стільки ж кінематичних рівнянь? А чи не можна спростити поставлене завдання – визначити положення твердого в просторі за допомогою мінімального числа координат і так, щоб ці координати незалежно від числа частинок в твердому тілі однозначно визначали його положення в просторі.

Для прикладу розглянемо тверде тіло у вигляді трикутника (рис. 1.2.2).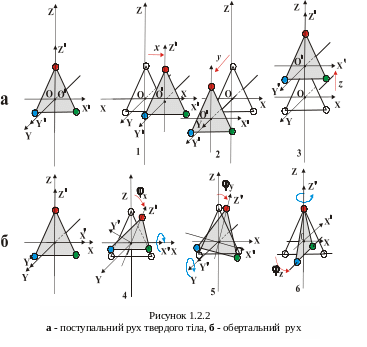

Тіло рухається в просторі відносно вибраної нами «нерухомої» системи відліку з координатами X,Y,Z. З самим тілом, як з тілом відліку, зв’яжемо іншу систему координат X´,Y´,Z´ початок якої( точка О) знаходиться в центрі мас даного тіла. Нехай спочатку початки систем X,Y,Z та X´,Y´,Z´ та їх осі співпадають, як вказано на рис. 1.2.2. Будь-яке складне переміщення в просторі твердого тіла можна розглядати як сукупність окремих переміщень або рухів. Так, якщо будь-яка пряма, проведена в тілі при його русі залишається паралельно сама собі, то такий рух називають поступальним. Такий поступальний рух ілюструє рис. 1.2.2а:

1 - паралельне переміщення вздовж осі X.

2 - паралельне переміщення вздовж осі Y.

3 - таке ж паралельне переміщення вздовж осі Z. Положення в просторі центра мас твердого тіла як матеріальної точки визначається трьома лінійними координатами X, Y, Z. При поступальному русі тіла всі його точки рухаються однаково (однаково змінюються всі координати X, Y, Z) і тоді положення твердого тіла в просторі можна визначити трьома координатами будь-якої точки даного тіла.

Крім поступального руху, тіло може здійснювати обертання, і для опису такого руху додаткові координати. Знову ж таки, нехай спочатку системи X, Y, Z та X´, Y´, Z´ та їх осі співпадають ( рис. 1.2.2б). Будь-який поворот у просторі твердого тіла можна подати як послідовність трьох незалежних поворотів, трьох обертань відносно трьох осей обертання, роль яких виконують осі X, Y, Z.

4 - обертання відносно осі X і таке обертання визначається кутовою координатою φх.

5 - кутова координата φy визначає обертання відносно осі Y.

6 - обертання відносно вісі Z, що характеризується відповідною кутовою координатою φz.

Таким чином, положення в просторі твердого тіла визначається шістьма координатами – трьома лінійними, які визначають положення центра мас тіла та трьома кутовими, що характеризують обертання цього тіла. Тілу дана своєрідна «свобода» у його переміщенні в просторі і ця свобода визначається мінімальним число незалежних координат, що визначають положення тіла в просторі, які отримали назву – числа ступенів свободи.

У даний час поняття числа ступенів свободи набуло особливо актуального значення у проектуванні та виготовленні механізмів, які називають маніпуляторами або навіть роботами. Основою маніпуляторів є механізми з багатьма ступенями свободи. Маніпулятори можуть виконувати роботи в середовищах або умовах, які недоступні для людини. Так, на рис.1.2.3 показано марсохід, який досліджував у автоматичному режимі поверхню Марса.

Цей марсохід надзвичайно складний апарат, який поєднує сучасну комп’ютерну техніку з найсучаснішою механічною частиною для його переміщення з так званою механічною рукою для взяття проб ґрунту. Звичайно, що такий марсохід як механічна система володіє великою кількістю ступенів свободи. Але з точку зору машин і механізмів людина, її біомеханіка є особливою механічною системою з величезним числом ступенів свободи. Для прикладу розглянемо спрощену модель ходьби людини, що схематично вказано на рис.1.2.4. Показаний лише один елемент ходьби у випадку опори на праву ногу (потім опорною буде ліва нога).

Будемо вважати, що тулуб людини здійснює поступальний рух і визначення положення центра мас (точка 1) тулуба достатньо три координати. Так само необхідно по три координати для визначення центра мас стегна (точка 2), гомілки (точка 3) та ступні (точка 4). Разом з тим, на рух центрів мас вказаних частин тіла припадає 12 ступенів свободи. Крім того, стегно, гомілка та ступня ноги повертаються. Якщо брати до уваги обертання лише в одній площині, то для лівої ноги необхідно ввести ще три кутові координати, а для правої опорної достатньо однієї кутової координати. Така, навіть спрощена, механічна модель ходьби людини має 16 ступенів свободи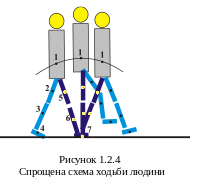. А тепер уявіть, яке загальне число ступенів свободи людського тіла. Самі проаналізуйте можливі рухи пальців руки – Ви нарахуєте не менше 14 ступенів поступального руху та 42 ступені свободи обертального руху. Недарма говорять, що рука людини – найдосконаліший механізм і навіть є приказка «руки все зроблять». Всіма цими рухами керує рефлекторна нервова система, яка знаходиться у спинному мозку, який є своєрідним комп’ютером, що здійснює механічні рухи. На щастя, природа потурбувалась про те, щоб ми не думали як треба підняти ногу і зігнути її, щоб здійснити крок. Ми бачимо, наприклад, перешкоду і її треба переступити. Око бачить цю перешкоду, дає сигнал нервовій системі і ця система вже без нашого відома мовою сучасної техніки аналізує цей сигнал і дає команду відповідним м’язам здійснити необхідні скорочення – підняти ногу, зігнути і т.п. Сучасні маніпулятори теж здійснюють подібні операції – наприклад, механічна рука, де роль м’язів виконують електродвигуни або гідравлічні системи, а керують ними комп’ютери. Згадайте фільм «Термінатор», коли рухалась лише металева механічна частина робота, а його основною частиною був чіп, який, по суті, був і головним і спинним мозком термінатора.

Отже, розглядаючи ступені свободи тіла, було виділено два основні рухи – поступальний та обертальний. Якщо в попередніх розділах в основному йшла мова про рух матеріальної точки, яким можна описати і поступальний рух твердого тіла, то на питанні обертального руху необхідно зупинитись більш докладно. Тому наступний розділ якраз і буде стосуватись кінематики обертального руху.