3.4 Реактивний рух в природі. Живі ракети
Р
еактивний
рух властивий деяким представникам
живої природи. Наприклад, кальмарам,
каракатицям, медузам – всі вони
використовують для плавання реакцію
струмини води, що відкидається. Так,
кальмар забирає у себе воду, а потім
виштовхує її через невеликий отвір, як
показано на рис.3.4.1, і, тим самим,
забезпечуючи реактивний рух. Все як у
реактивному двигуні – тільки замість
газів витікає вода зі швидкістю
,
а сам кальмар рухається у протилежному
напрямі з швидкістю
(приблизно 70 км/год).
При цьому всі щупальці кальмара
збираються у вузол, і він набуває обтічної
форми.
Другий разючий приклад реактивного руху в природі – це, так званий, скажений огірок. Природа справді створила живу рослинну ракету. У південних країнах та у нас на узбережжі Чорного моря виростає рослина під назвою "скажений огірок". Цю рослину не дарма так називають. До моменту стиглості в ньому виникає великий тиск (майже 6 атмосфер). Навіть легкий дотик до такого огірка викликає неймовірний ефект – миттєво огірок відривається від стеблини, а з отвору, що утворився, викидається сильна струмина клейкої рідини з насінням. Летить такий огірок, подібно ракеті (рис3.4.2), розкидаючи насіння на відстань майже 12 м.
3.5 Робота сталої і змінної сил. Потужність
Ми настільки звикли до терміну „робота”, що для нас це поняття не вимагає пояснення. Але що ж таке робота? Якщо говорять – у нього важка фізична робота, то мають на увазі, що під дією мускульної сили переміщаються важкі предмети. Наприклад, робітник працює вантажником. Але такий самий результат переміщення тіла можна отримати за рахунок не мускульної, а іншої сили, наприклад, електродвигуна підіймального крана. Таким чином, дія сили, однаковою за величиною, але різною за своєю природою, в першому і другому випадках однакова. Отже, доцільно ввести фізичну величину, яка б характеризувала дію сили при переміщенні, і тому в механіці мірою дії сили при переміщенні тіла є фізична величина, що називається роботою.
Спочатку розглянемо
найпростіший випадок переміщення тіла
під дією сталої сили. Наприклад, на тіло
діє стала сила
,
під дією якої відбувається переміщення,
модуль якого дорівнює
,
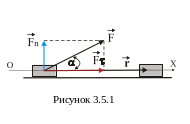
як вказано на рис.3.5.1. Очевидно, чим
більша сила і чим більше переміщення,
тим більша дія такої сили, тобто робота.
Отже, робота сили повинна визначатись
добутком сили на переміщення. А якщо
напрям сили не співпадає з переміщенням?
Звичайно, тоді роботу виконує тангенціальна
(дотична)
,
складова сили, що співпадає з переміщенням,
і тоді робота сталої сили визначається
відомим співвідношенням
,
(3.5.1)
де
– кут між напрямом сили і переміщенням.
Зрозуміло, що нормальна (перпендикулярна)
складова
роботи не виконує.
Одиницею роботи в системі СІ є 1 Дж (джоуль), який дорівнює роботі, здійснюваній силою 1Н на шляху 1м.
Скалярний добуток
можна переписати у вигляді добутку
проекції сили
на напрям переміщення
.
(3.5.2)
Якщо робота
виконується змінною силою, то спочатку
визначають елементарну роботу
на такому малому переміщенні,
,
щоб силу вважати сталою і ця елементарна
робота дорівнює
.
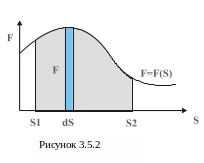
(3.5.3)
Тоді вся робота дорівнює інтегральній сумі
.
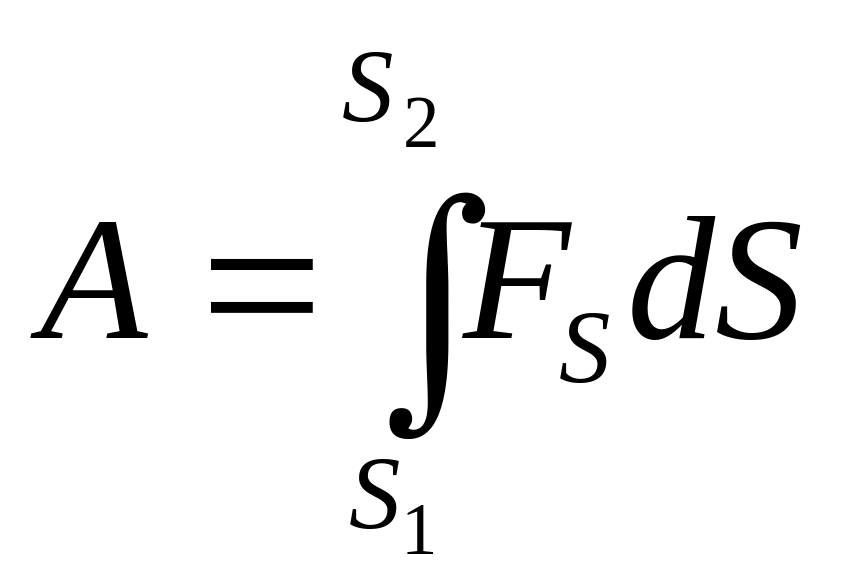(3.5.4)
Наприклад, залежність сили від шляху задана деякою функцією, графік якої наведений на рис. 3.5.2.
Як видно з рис.3.5.2, елементарна робота чисельно дорівнює площі смужки з основою і висотою F, а вся робота буде чисельно дорівнювати сумі площ, тобто площі цієї криволінійної фігури.
Як найпростіший
випадок роботи змінної сили можна
розглядати роботу при деформації
пружини, яка виконується силою,
пропорційною зміщенню
.
Тоді робота такої змінної сили дорівнює
.
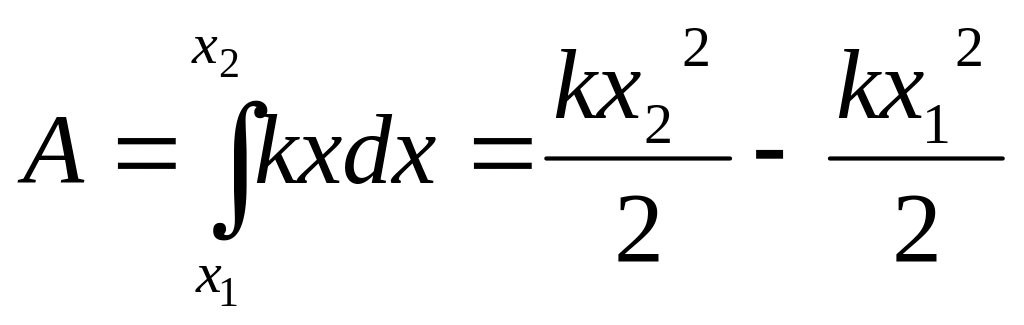(3.5.5)
Визначаючи
елементарну роботу
,
ми користуємось математичним знаком
диференціала
.
З математики відомо, що лише неперервна
функція диференційована в кожній точці.
А чи може робота, як неперервна функція,
існувати в „точці”?
Звичайно, ні. Отже, робота не є функція
стану, вираз
не є повним диференціалом неперервної
функції, а вираз
– це є елементарна робота, тобто робота
при нескінченно малому переміщенні
(але
ні в якому випадку в точці).
Одна і та ж робота може бути виконана за різні проміжки часу, тому вводять фізичну величину, яка називається потужністю. Якщо за будь-які, але рівні проміжки часу, виконується однакова робота, то відношення цієї роботи за той час, за який дана робота виконана, називається потужністю.
.
(3.5.6)
Якщо за рівні
проміжки часу
виконується неоднакова робота
,
то відношення
(3.5.7)
дає значення середньої потужності. Миттєва потужність визначається відношенням елементарної роботи за час до цього часу .
.
(3.5.8)
Так як
,
то
.
(3.5.9)
Наприклад,
–
сила тяги двигуна,
– швидкість.
В системі СІ одиницею потужності є Вт (ват), 1Вт = 1 Дж/с. Поряд з цією одиницею потужності інколи (особливо для двигунів) користуються несистемною одиницею потужності – одна кінська сила, 1к.с. = 736 Вт.