2.3.2 Експериментальне визначення гравітаційної сталої. Дослід Кавендиша

Фізичний зміст гравітаційної сталої в законі тяжіння Ньютона дуже простий, про що вказувалось в попередній темі. Так, з цього закону гравітаційна стала визначається наступним співвідношенням

. (2.3.9)

Але для цього необхідно знати числові значення всіх величин, що входять в це співвідношення, необхідно їх виміряти. Якщо вимірювання мас тіл та відстаней між ними особливих труднощів не складає, то вимірювання сил притягання – складна експериментальна задача. Майже у всіх підручниках фізики читаємо стандартну фразу «вперше гравітаційну сталу було визначено в 1798 році англійським фізиком Кавендишем за допомогою крутильних терезів» (дається короткий опис експерименту та вказується отриманий результат G=6,67·10^-11(Н·м²)/кг². Так то воно так, але трішечки не так (крилата фраза Шельменко-денщика, українського Фігаро). Це трішечки «не так» полягає в тому, що це зовсім не так. Кавендиш в своїх дослідах не визначив гравітаційну сталу, а масу Землі, точніше її густину, порівнюючи її з густиною води. Виникає питання, а чому Кавендиш не визначив гравітаційну сталу. Банальна відповідь – він не знав про її існування. Так, не знав і не міг знати. Перенесемося в кінець 18 століття, коли ще не було єдиної системи фізичних одиниць. Хоч як би хотів Кавендиш визначити гравітаційну сталу, її просто в той час не існувало, адже для її фізичного тлумачення потрібна одиниця сили. Лише згодом в 1832 німецьким фізиком Гаусом була встановлена перша система фізичних одиниць і першою одиницею сили була дн (дина) – це така сила яка надає тілу масою 1г прискорення 1 м/с² (порівняйте з одиницею сили 1Н). Так в чому ж таки заслуга Кавендиша, якщо він не визначив числового значення гравітаційної сталої? А заслуга надзвичайно велика – визначивши масу Землі, Кавендиш дав можливість при появі єдиної системи фізичних величин легко розрахувати в цій системі гравітаційну сталу.

Так все ж таки, як Кавендиш визначив густину Землі, не знаючи про єдину систему фізичних величин, якої на той час і не було. Тут Кавендиш, користуючись мовою сучасної науки і техніки, використав принцип фізичного моделювання. Щоб зрозуміти ідею такого моделювання дещо видозмінимо деталі досліду Кавендиша, залишаючи без змін сам принцип досліду. Тобто, якщо тіло масою m притягається до Землі, як кулі масою М_З та радіуса R_З з силоюF_З , то це ж тіло в лабораторних умовах буде притягатись до кулі масою М та радіуса R з силоюF. Тобто, маємо модель Землі. В дослідах Кавендиша такою своєрідною моделлю Землі були свинцеві кулі діаметром 20 см і масою 49,5 кг, а тіло, що зазнає притягання – свинцева кулька діаметром 5 см та масою 775 г.

Знаючи закон тяжіння, Кавендиш міркує так: сила притягання зі сторони Землі в стільки разів більша, в скільки разів маса Землі більша маси моєї кулі, а, враховуючи квадратичну залежність сили тяжіння від відстані, будемо мати наступне відношення:

. (2.3.10)

Звідки маса Землі дорівнює

. (2.3.11) Отже дійсно, для визначення маси Землі в дослідах Кавендиша зовсім не потрібне значення гравітаційної сталої. Тому інколи дослід Кавендиша називають дослідом «зважування Землі» і, найголовніше, що немає потреби визначати абсолютні значення сил тяжіння, треба знати їх відношення. Але як це зробити? Якщо йде мова про порівнянне вимірювання двох однойменних фізичних величини, то найкраще проводити їх вимірювання одним і тим же приладом, тут абсолютні значення величин нам не потрібні, наприклад, шкала в приладі Кавендиша була проградуйована в дюймах, а ми б градуювали в міліметрах, від цього відношення лінійних величин не змінюється – відношення дюйм на дюйм таке саме як міліметр на міліметр. Що стосується конструкції самого приладу, то він повинен бути, мовою сучасної техніки, приладом з широким діапазоном вимірювань – починаючи від надзвичайно слабої гравітаційної взаємодії свинцевої кулі масою М з кулькою масою m і закінчуючи таки добре відчутною силою притягання цієї ж кульки до величезної кулі, якою є Земля. Ці вимоги найкраще здійснити за допомогою крутильних терезів, де незначне кутове переміщення може бути «підсилене» зміщенням променя світла відбитого від дзеркала, яке закріплене на рухомій частині приладу. Поетапно розглянемо принцип досліду Кавендіша, що ілюструє рисунок 2.3.6

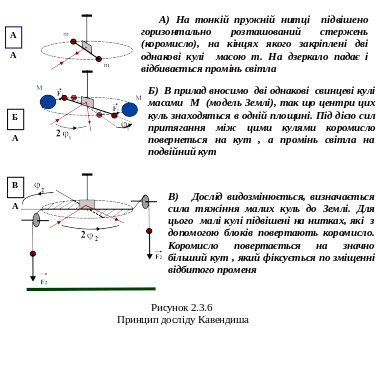
Саме горизонтальне розташування коромисла в дослідах Кавендиша дало можливість в «чистому» виді визначити силу притягання між свинцевими кулями, виключаючи силу притягання до Землі. При горизонтальному розташуванні коромисла сила тяжіння до Землі перпендикулярна до напряму переміщення куль і не може викликати їх обертання, і ця сила пропорційна куту повороту коромисла. В дослідах Кавендиша визначалось зміщення відбитого променя на шкалі приладу з точністю 0,02 дюйма ( 1 дюйм відповідає 2,54 см). Отже, якщо малі кулі притягаються до великих з силою , то це і викликає зміщення променя по шкалі приладу на k₁ дюймів, а сила притягання тих же самих куль, тільки тепер до Землі зміщується промінь на k₂ дюймів. Вважаючи пропорційність цих зміщень до сил, відношення сил у випадках А та В (рис.2.3.2.1) можна замінити відношенням зміщень відбитого променя в приладі Кавендиша . (2.3.12)

Отже, шукана маса Землі дорівнює

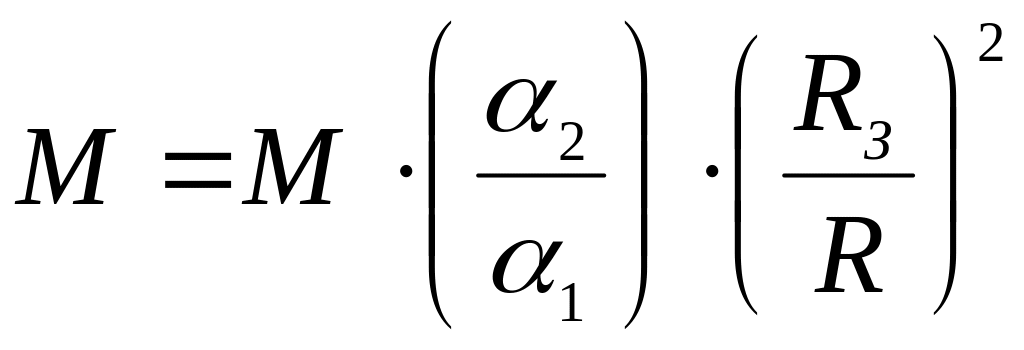(2.3.13)

Ми розглянули лише принцип досліду Кавендиша, опускаючи окремі технічні деталі досліду. Прилад Кавендиша, мовою сучасної техніки, був крутильними терезами з широким діапазоном вимірювань який забезпечувала система блоків (рис.2.3.7).

К рім того, весь прилад Кавендиш встановлював у закриту кімнату, щоб усунути можливу дію потоків повітря, а за поворотом коромисла спостерігав за допомогою підзорної труби, як це показано на рис.2.3 Гравітаційна стала є однією з фундаментальних фізичних величин, але по сьогоднішній день така фундаментальна фізична визначена найменш точно. Причина проста – в лабораторних умовах поки що неможливо з високою точністю визначити слабу гравітаційну взаємодію. Вона стає помітною для тіл великої маси. Але тоді виникають проблеми з вимірювань мас цих тіл. Якщо намагатися визначити G з руху планет і супутників, то необхідно з високою точністю знати маси планет, а вони визначені далеко не точно. Тому і на даний час визначення гравітаційної сталої проводиться класичним методом вимірювання в лабораторних умовах сил гравітаційної взаємодії між тілами відомої маси, в основному за допомогою торсійних терезів. Вигляд таких сучасних торсійних терезів, які використовуються у Вашингтонському університеті наведений на рис.2.3.9. Вимірюється сила тяжіння між двома підвішеними усередині пластинами (на фотографії не видні) і кулями, розташованими на периферії циліндра і отримане значення гравітаційної дорівнює G=(6,67390·10^-11 ± 0,00001) (Н·м²)/кг² .