4.6. Симметрия молекул

В многоатомной молекуле можно выделить одинаковые атомы, химические связи либо отдельные фрагменты (группы атомов). Их взаимное пространственное расположение придает молекуле определенную структурную форму, которая может быть подобна некоторой геометрической фигуре. Ввиду наличия в молекуле одинаковых частей (атомов), которые можно взаимозаменять в результате различных поворотов, отражений, говорят, что молекула в устойчивом электронном состояния обладает определенной симметрией равновесной конфигурации ядер. Атомы либо структурные группы, которые можно менять местами, эквивалентны по своей симметрии. Молекула может обладать одним или несколькими элементами симметрии (например, ось симметрии, плоскость симметрии и др. (рис. 4.6)). Каждому элементу симметрии соответствует своя операция симметрии, при которой равновесная конфигурация молекулы пер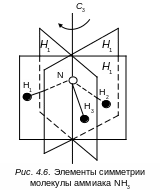 еходит сама в себя. Эквивалентными атомами или связями в молекуле будут такие атомы или связи, которые могут взаимозаменяться в результате операций симметрии. Все атомы данного вида, а равным образом и химические связи, эквивалентные в отношении симметрии, являются химически тождественными.

Например, в результате поворота молекулы NH₃ на угол 120° вокруг оси третьего порядка (С₃), проходящей через атом азота (рис. 4.6.), получим конфигурацию, эквивалентную первоначальной, так как атомы водорода и связи N–H считаются одинаковыми. Следующий поворот на 120⁰ переводит молекулу NH₃ в новое положение, неотличимое от предыдущего. В общем случае молекула с осью симметрии n-го порядка имеет n эквивалентных положений, получающихся одно из другого вращением вокруг этой оси. Операцию вращения рассматривают как операцию симметрии.

Все операции симметрии для молекулы оставляют хотя бы одну точку в пространстве без изменения. Обычно в этой точке пересекаются все оси и плоскости симметрии, поэтому она является центром симметрии (центром тяжести молекулы). Наличие элементов симметрии и соответствующих им операций симметрии позволяет разбить все молекулы по числу и характеру их элементов симметрии на небольшое число групп. Эти группы называются точечными группами симметрии. Точечными потому, что при проведении любой операции симметрии в молекуле всегда имеется хотя бы одна точка, положение которой не меняется при проведении любой операции симметрии, присущей молекуле

4.6.1. Группа. Определение и основные свойства

Впервые понятие группы было введено в математике для описания такой совокупности элементов а, b, с, d, ...., которая подчиняется определенным групповым законам. Природа этих элементов может быть самой разнообразной. Это могут быть числа, перестановки, операции симметрии и др.

Основные законы теории групп можно сформулировать следующим образом:

1. Произведение двух элементов а и b группы дает третий элемент c, принадлежащий группе, т. е.

с = b a. (4.32)

Произведение здесь понимается в обобщенном смысле как комбинация или сочетание двух элементов, которое по определенным правилам дает третий элемент. Это произведение зависит от порядка элементов. Если под a и b понимать операции симметрии, то при записи b a, сначала выполняется операция a, а затем операция b. Обратное не всегда cправедливо. Иначе говоря, для элементов группы коммутативный закон не всегда выполняется, т. е.

ba  ab.

2. Совокупность элементов группы содержит единичный элемент I, для которого выполняется правило

aI = Ia = a. (4.33)

Под a здесь понимается любой элемент группы. Для операций симметрии под единичным элементом будем понимать поворот системы на угол, равный нулю (С₁) или 360°.

3. Совокупность содержит обратный элемент. Например, элементу а имеется обратный элемент а^–1 такой, что

a a^–1= a^–1 a = 1. (4.34)

Для каждой операции симметрии всегда имеется обратная операция, которая уничтожает действие первой. Например, повороту системы на угол  по часовой стрелке всегда найдется обратная операция – поворот той же системы на угол –  (против часовой стрелки).

4. Для элементов группы всегда выполняется так называемый ассоциативный закон

c(ba) = (cb), (4.35)

т. е. безразлично умножается сначала a на b, а затем получаемое произведение ba умножить на c, либо умножается a на произведение b на c (т. е. cb). В силу cказанного произведение трех элементов группы можно записывать в виде cba.

Все группы разделяются на конечные и бесконечные в зависимости от того, сколько элементов они содержат. Число элементов в группе называют ее порядком h. Пример группы бесконечного порядка – это число поворотов вокруг оси связи на любой угол в двухатомной молекуле. Эта группа будет являться не только бесконечной, но и непрерывной, т. е. ее элементы (повороты) непрерывным образом зависят от угла , который может принимать любые значения от 0 до 2.

Важным понятием является подгруппа, под которой понимают часть элементов группы, удовлетворяющая групповым условиям.

Группы, для которых выполняется закон коммутативности, т. е. ba = ab, называются абелевыми (в честь норвежского математика Абеля). Все другие группы будут неабелевы, или некоммутативны.

Для молекул мы будем иметь дело с точечными группами симметрии, т. е. такими группами, операции симметрии которых оставляют хотя бы одну точку в пространстве неподвижной. Обычно эта точка является центром тяжести молекулы.