4.3. Нормальные координаты и колебания.
Как
было показано в
п. 4.2,
значения кинетической и потенциальной
энергии колеблющейся молекулы были
выражены через произведение скоростей
и произведение qiqk
координат.
Однако, характеристическое уравнение
и уравнение для нахождения амплитуд
колебаний
можно упростить, если ввести такое
преобразование координат, в результате
которого все коэффициенты Аik
и Kik
обратятся в
нуль для i
k
и останутся только те коэффициенты, для
которых i
= k.
Можно показать математически, что такие
координаты действительно существуют.
Обозначим их через Q1,
Q2,
..., Qn.
Они определяются через координаты
смещения qk
с помощью линейных уравнений
,
(4.14)
где Cik – квадратная матрица, элементы которой подбираются так, чтобы в новых координатах кинетическая и потенциальная энергия имели вид
(4.15)
В развернутом виде это может быть записано так:
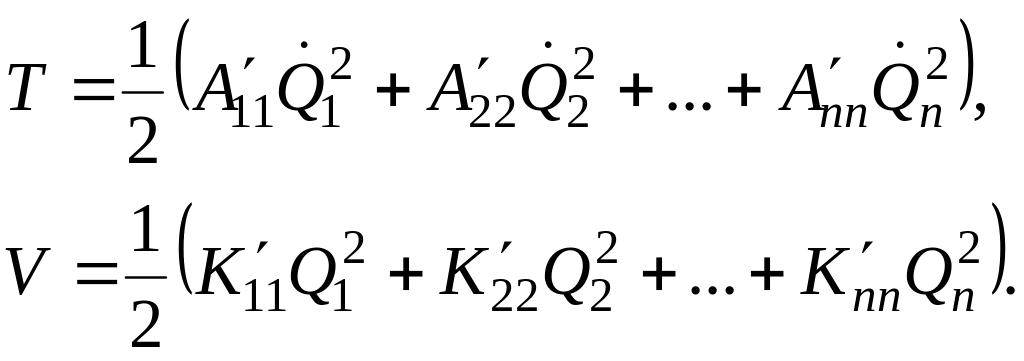(4.16)
Другими
словами, в выражения для кинетической
и потенциальной энергии в нормальных
координатах входят только квадраты
скоростей
и квадраты координат Q
без перекрестных членов. С физической
точки зрения это означает, что каждая
такая координата изменяется независимо
от других координат в процессе колебания.
Координаты Qi, удовлетворяющие введенным выше условиям, называются нормальными координатами, а колебания молекулы представленные в этих координатах, называются нормальными (главными) колебаниями. Уравнение движения в этих координатах получится в виде, аналогичном (4.7), т. е. уравнение движения Ньютона в форме Лагранжа запишется в виде:
.
(4.17)
Итак, вместо (4.17) можно написать n уравнений по числу колебательных степеней свободы вида
или
(4.18)
где
– квадрат частоты собственных колебаний
молекулы (i
=
1, 2, 3, ... n).
Как видно, уравнение (4.18) описывает
гармонические колебания системы атомов
в молекуле. Решение уравнения (4.18),
как следует из теории гармонического
осциллятора, можно записать в виде
,
(4.19)
где i, – частота, совпадающая с одной из частот колебаний молекулы, Qi0 и i, – амплитуда и фаза этого колебания.
Таким образом, из уравнения (4.18) видим, что колебания молекулы в нормальных координатах – это гармонические колебания, которые совершаются с собственными частотами i. Уравнение движения в нормальных координатах для молекул распадается на n независимых уравнений гармонических колебаний. Каждая нормальная координата совершает независимое гармоническое колебание.
Матрицы кинетической и потенциальной энергии в нормальных координатах преобразуются к диагональной форме, а полная энергия
(4.20)
равна сумме энергий Ei гармонических осцилляторов, колеблющихся по закону (4.19). Следовательно, любое колебательное движение системы (молекулы) может быть представлено как наложение нормальных колебаний с соответствующими амплитудами. Для наглядности формы колебаний часто изображают стрелками около атомов, передающими направления смещения при возбуждении одного из нормальных колебаний. Длина стрелки характеризует величину этих смещений.