Глава 2. Вращательные спектры молекул

2.1. Вращение двухатомной молекулы. Классический случай

рассмотрим двухатомную молекулу, состоящую из двух ядер на некотором расстоянии , которое назовем равновесным, и обращающиеся вокруг ядер электроны. Связь между атомами в такой молекуле обусловлена электрическими силами взаимодействия между заряженными частицами (электронами и ядрами). Несмотря на то, что двухатомная молекула представляет собой некоторую динамическую систему из движущихся электронов и ядер, для простоты изучения картины вращения рассмотрим ее упрощенную модель. Согласно этой модели, молекула представляется в виде жесткого образования, по форме напоминающего гимнастическую гантель (см. рис.2.1).

С точки зрения вращения она представляет собой жесткий ротатор (расстояние между атомами постоянно). Вращается указанная система вокруг осей, проходящих через центр тяжести. Общее число таких осей равно трем. Однако вращение вокруг оси, проходящей через ядра атомов, не приводит к изменению энергий. Ядра считаются точечными, а массой электронов по сравнению с массой ядер пренебрегают, поэтому момент инерции вокруг указанной оси равен нулю. В двухатомной молекуле будем учитывать две различные оси вращения (OO₁ и OO₂), перпендикулярные оси молекулы, т. е. две вращательные степени свободы.

Для описания движения построенной модели двухатомной молекулы как целого необходимо получить выражения ее кинетической (Т) и потенциальной (V) энергий для данного вида движения (вращения). зная выражения, составим уравнение движения и решим его. В результате получим значения координат как функций времени, т. е. законы движения рассматриваемой модели.

Поскольку, для жесткого ротатора const и потенциальная энергия V = const, которую можно положить равной 0, тогда полная энергия Е ротатора равна кинетической энергии вращающихся масс m₁ и m₂ вокруг одной из осей (OO₁ или OO₂), т. е.

(Е = Т, так как V = 0) (2.1)

где и – линейные скорости движения атомов, находящихся на расстоянии r₁ и r₂ от оси вращения. Вводя вместо линейной скорости угловую  ( и ), выражение (2.1) можно переписать следующим образом:

, (2.2)

где выражение в скобках есть сумма моментов инерции I₁ и I₂ вращающихся атомов относительно оси вращения, r₁ и r₂ – расстояния массы атомов от оси вращения.

Можно показать, что , где – приведенная масса молекулы, а – равновесное расстояние между атомами. Предоставляем это проделать читателю.

С учетом сказанного равенство (2.2) можно переписать следующим образом:

, (2.3)

где I – момент инерции двухатомной молекулы. Таким образом, кинетическая энергия вращающейся молекулы пропорциональна квадрату угловой скорости и является функцией температуры. Это свидетельствует о том, что молекула может вращаться с любой скоростью , определяемой температурой среды.

Поглощать или испускать радиацию могут те молекулы, у которых при вращении будет изменяться дипольный момент. Известно, что дипольный момент есть вектор. Он может изменяться и по величине, и по направлению. Так как расстояние между атомами в двухатомной молекуле принимается постоянным (жесткий ротатор), то при вращении молекулы дипольный момент изменяется только по направлению. Следовательно, поглощать или испускать радиацию будут те молекулы, которые обладают постоянным дипольным моментом. К таким относятся все молекулы, состоящие из неодинаковых атомов (например, СО NO, HCl и др.). У них центр тяжести положительных зарядов не совпадает с центром тяжести отрицательных зарядов. Все бездипольные молекулы, состоящие из одинаковых ядер, не обладают чисто вращательными спектрами поглощения и испускания. Эти молекулы имеют достаточно высокую симметрию ( ), и у них центры тяжести положительных и отрицательных зарядов совпадают, т. е. отсутствует дипольный момент.

При комнатной температуре значительная часть молекул находится на сравнительно высоких (возбужденных) уровнях вращатель­ной энергии. Распределены они по этим уровням в соответствии с законом Больцмана. Доля молекул, имеющих вращательную энергию в интервале от Е_вр до Е_вр + dЕ_вр, выражается формулой

, (2.4)

где dЕ_вр= I_врd_вр с учетом выражения (2.3), А – некоторая постоянная величина.

Пусть полное число молекул в единице объема с любыми вращательными энергиями равно n₀. Это же число молекул мы можем найти, пользуясь выражением (2.4), если проинтегрируем по всем вращательным энергиям от 0 до .

, (2.5)

откуда A = n₀/kT.

С учетом постоянной А формулу (2.4) можно переписать следующим образом:

. (2.6)

Классическое распределение интенсивностей во вращательной полосе совпадет с распределением молекул по различным вращательным состояниям, определяемым формулой (2.6), и графически представлено на рис. 2.2.

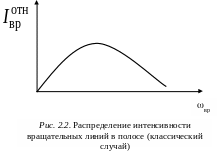
Так как по классической теории частоты _вр могут изменяться непрерывно, то полоса должна быть сплошной.