4.6.3. Точечные группы симметрии и их элементы

В точечных группах симметрии молекул операции симметрии группируются по классам. Говорят, что две (и более) операции относятся к одному классу, если их можно получить некоторым преобразованием координат, состоящим из операций симметрии данной точечной группы. Например, три отражения в плоскостях , и в молекуле NH₃ принадлежат к одному классу, поскольку их можно реализовать, поворачивая систему координат на 120°. Из определения классов следует, что в один класс входят следующие пары операций:

1) два поворота на одинаковый угол вокруг разных осей, если в группе имеется операция, переводящая одну ось в другую;

2) два поворота и вокруг одной оcи, если в группе есть операция поворота, меняющая направление оси на обратное, либо операция отражения в плоскости, содержащей ось С_n;

3) два отражения в разных плоскостях, если в группе имеется операция, переводящая одну плоскость в другую.

Например, мы видели, что наличие у молекулы оси S₂ эквивалентно наличию центра симметрии i.

i  S₂= _hС₂. (4.37)

Отметим, что операции C_n и _h коммутируют. При нечетных n (n =  2m + 1) из (4.37) получаем (с учётом )

; ; . (4.38)

Это означает, что система обладает в данном случае как осью С_n так и плоскостью _h (в отдельности). Таким образом, лишь при четном n S_n представляет собой самостоятельный элемент симметрии. Заметим также, что в этом случае ось S_n одновременно является и осью С_n/2 (порядка n/2).

Сочетание в одной системе нескольких различных элементов симметрии автоматически приводит к появлению новых элементов симметрии. Так, линия пересечения двух взаимно перпендикулярных плоскостей симметрии всегда является осью симметрии молекулы (например, H₂O). Чем больше число различных элементов симметрии (и их комбинаций), тем выше симметрия молекулы (например, С₆Н₆). Вообще говоря, особенность точечных групп заключается в том, что все они могут быть построены из простейших групп С_n путем присоединения новых элементов симметрии. Причем это добавление не может быть произвольным (например, новые оси симметрии не могут пересекаться со старыми осями под произвольными углами). Данное обстоятельство и служит причиной существования конечного числа точечных групп, а именно: C_n, S_n, C_nh, C_n, D_n, D_nh, D_nd, T, T_h, T_d, O, O_h, I, I_h. При этом каждая молекула принадлежит к одной точечной группе, являющейся строго определенной. Для конкретной точечной группы (молекулы) получаются вполне определенные типы симметрии состояний последней. Впервые полную классификацию групп симметрии молекул и кристаллов дал знаменитый русский кристаллограф Е. С. Федоров.

Число элементов группы h называется ее порядком (речь идет, естественно, о конечных группах в отличие от бесконечных). Задание группы определяется перечислением ее элементов и указанием закона их умножения (для конечных групп это делается в виде таблицы умножения). Во многих случаях, однако, более удобным оказывается задание группы с помощью указания образующих элементов (так называемых генераторов) и определяющих соотношений между ними. Для одной и той же группы генераторы можно выбирать разными способами. для каждого такого набора будут соответственно свои определяющие соотношения.

Рассмотрим вначале в самом общем виде как задаются перечисленные выше 14 точечных групп, а затем более подробно проанализируем их образование и свойства.

Группа С_n состоит из поворотов вокруг оси на углы 2m/n (m = 0, 1, 2, ..., n–1, где n – число элементов) и имеет один генератор С_n, а определяющее соотношение равно

. (4.39)

Группа С_nh имеет ось n-го порядка и перпендикулярную к ней плоскость отражения _h (рис. 4.10, а) и состоит из:

1) элементов группы (m = 1, 2,...< n–1);

2) n зеркально-поворотных преобразований: .

Генераторами группы являются С_n, _h, а определяющие соотношения имеют вид

. (4.40)

При четных n в группе есть инверсия , которая может быть выбрана в качестве генератора вместо _h

Группа S_n имеет одну зеркально-поворотную ось n-го порядка. При нечетном n она является группой C_nh, при четном n = 2m (определяющее соотношение). Порядок группы равен h.

Группа C_n содержит ось n-го порядка и n плоскостей отражения, проходящих через эту ось (рис. 4.10, б). Состоит из 2n элементов: n из них являются поворотами С_n , а оcтальные – отражениями _ в n вертикальных плоскостях. Генераторами группы служат С_n и _, а определяющие соотношения имеют вид

. (4.41)

Группа D_n имеет ось n-го порядка и n перпендикулярных к ней осей, которые обозначают С₂ (или V₂) (см. рис. 4.10, в). Группа содержит 2n элементов: n операций C_n, и n поворотов вокруг осей С₂. Генераторами группы служат С_n и C₂, а также соотношения

. (4.42)

Группа D_nh получается из группы D_n путем добавления плоскоcти отражения _h, перпендикулярной к оси С_n (см. рис. 4.10 г). Она состоит из 4n элементов: 2n операций группы D_n, произведений С_n_h и C₂C_n_h. Генераторы этой группы – С_n, C₂, _h (при четном n вместо _h можно использовать инверсию i). Определяющие соотношения

(4.43)

Группа D_nd получается из группы D_n путем добавления диагональных плоскостей отражения _d проходящих через ось С_n посередине между осями С₂ (рис. 4.11 д). Содержит 4n элементов: 2n элементов подгруппы D_n, n отражений в различных плоскостях (m = 0, 1, 2, ..., n – 1) и n произведений . Данную группу можно получить и из группы S_2n добавлением к ней оси второго порядка C₂ или плоскости отражения _. Генераторами служат S_2n и C₂. Определяющие соотношения:

. (4.44)

Группа Т есть группа вращений, совмещающих тетраэдр сам с собой, (рис. 4.11, а). Она содержит три взаимно перпендикулярные оси второго порядка, соединяющие середины противоположных ребер тетраэдра, и четыре оси третьего порядка, проходящие через каждую из вершин и центры противоположных граней. Эту группу можно получить из группы D₂ присоединением оси третьего порядка. Группа Т имеет 12 элементов: I, 3C₂, 4C₃ и 4 из вершин и центры противоположных граней. Ее генераторами являются С₂ и С₃, а определяющие соотношения имеют вид:

.

Группа Т_h получается из группы Т добавлением инверсии в центре тетраэдра. Так как С_2i = _h, то в группе появляются три взаимно перпендикулярные плоскости отражения.

Группа T_d (см. рис. 4.11, б) получается на группы Т добавлением шести плоскостей симметрии, проходящих (каждая из них) через две оси третьего порядка С₃, и одну ось второго порядка С₂. Она содержит 24 элемента: I, 4C₃, 4 , 6, 3C_4, 3 , 3C₂. Генераторами служат S₄, C₃. Определяющие соотношения имеют вид

S₄⁴= I; = I; S₄C₃S₄ = . (4.45)

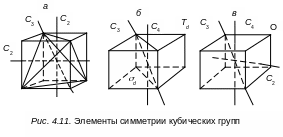
Группа О есть группа поворотов, совмещающих куб с самим собой. Она cодержит три оси четвертого порядка С_4, проходящие через центры противоположных граней, четыре оси третьего порядка С_3, проходящие через противоположные вершины куба, и шесть осей второго порядка С₂, проходящих через середины противоположных ребер (рис. 4.11 в.). Группа состоит из 24 элементов: I, 4C₃, 4 , 3C_4, 3 , 3 , 6C₂, В качестве генераторов можно выбрать C₄ и C₃, которые удовлетворяют следующим cоотношениям:

= I; = I; C₄C₃C₄ = . (4.46)

Группа O_h получается добавлением к группе О центра инверсии. Число элементов равно 48: I, i, 4C₃, 4 , 4S₆, 4 , 3C₄, 3 , 3 , 3S₄, 3 , 6C₂, 3_h, 6_d. Для этой группы генераторами можно выбрать поворот С₄ и зеркальный поворот S₆, которые удовлетворяют соотношениям

= I; = I; C₄ = C₄; S₆ S₆ = С₄.

Группы симметрии икосаэдра I, I_h. Поскольку молекулы данных групп встречаются крайне редко, на детальной их характеристике не будем останавливаться.

Помимо перечисленных групп, устремив порядок оси С₄ к бесконечности, легко получим так называемые непрерывные точечные группы: С_, C_h, С_,D_, D_h. Все точечные группы молекул по порядку осей, содержащихся в них, можно разделить на три вида:

1) низшей симметрии, соответствующей молекулам с осями симметрии С_n и n не выше 2(C₁, C₂, D₂, D_i, C_i, C_s, C_2h, C_2, D_2h);

2) средней симметрии, соответствующей молекулам с выделенной осью симметрии с n  3(C_n, D_n, C_nh, C_n, D_nh, S_n, D_nd, C_h, D_h);

3) высшей симметрии кубические группы, соответствующие молекулам с несколькими осями симметрии с n  3(T, T_h, T_d, O, O_h).

С принадлежностью молекулы к определенному виду групп симметрии тесно связaна возможность вырождения ее уровней энергии. Так, молекулы групп низшей симметрии имеют только невырожденные состояния. В группах средней симметрии наряду с невырожденными появляются и двукратно вырожденные состояния. Тройное вырождение уровней энергии имеет место в группах высшей симметрии.

Весьма существенной характеристикой молекулы с точки зрения формирования оптического спектра является наличие или отсутствие у нее дипольного момента. Последнее же непосредственно связано с симметрией молекулы. Для молекул, имеющих дипольный момент и обладающих определенной симметрией, его направление частично или полностью определяется этой симметрией.

Другой важной характеристикой молекулы является ее поляризуемость, определяемая симметричным тензором поляризуемости _(, =x, y, z) с составляющими _xx, _yy, _zz, _xy = _yx; _yz = _zy; _xz = _zx Наличие симметрии накладывает определенные условия на тензор поляризуемости, что существенно сказывается на правилах отбора в спектрах комбинационного рассеяния.

В заключение рассмотрим табл.4.1, в которой несколько по-другому сопоставлены и охарактеризованы наиболее важные из возможных групп симметрии и примеры соответствующих молекул.

Таблица 4. 1