2.2. Квантовомеханический случай

Совсем по-иному подходит квантовая механика для нахождения энергии жесткого ротатора. Общий квантовомеханический подход для нахождения энергии заключается в решении уравнения Шредингера для жесткого ротатора

, (2.7)

где – оператор Гамильтона для жесткого ротатора, ψ_вр – вращательная волновая функция, Е_вр – собственное значение энергии оператора.

Учитывая, что для жесткого ротатора можно считать его потенциальную энергию V = 0, оператор Гамильтона будет равен только оператору кинетической энергии такой системы. Уравнение Шрёдингера для стационарных состояний жесткого ротатора формально будет совпадать с уравнением движения свободной частицы с кинетической энергией Т и массой m:

, (2.8)

где – оператор кинетической энергии частицы, – оператор Лапласа. символ (набла в квадрате) означает оператор, определяемый соотношением . Для вращающегося ротатора это уравнение можно переписать следующим образом:

, (2.9)

где  приведенная масса вращающейся молекулы. Если это уравнение переписать в сферических координатах r, ,  связанных с декартовыми координатами x, y, z соотношениями x = rsin sin, y = rsincos, z = rcos, то оно примет вид:

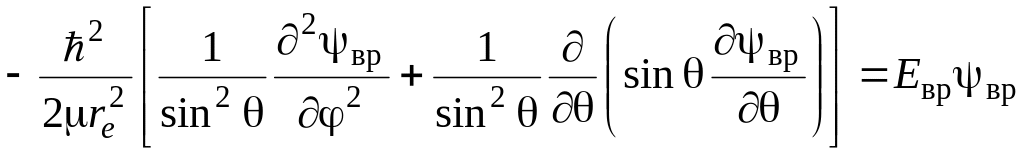. (2.10)

Здесь учтено то обстоятельство, что из общего выражения Лапласиана

,

первый член равен нулю, так как радиальная координата не изменяется в процессе вращения (жесткий ротатор). поэтому вращательная волновая функция зависит только от угловых координат  и , а значение r равно . Таким образом, вращение двух масс m₁ и m₂ вокруг одной из осей, проходящих через центр тяжести системы, мы заменяем вращением массы . (приведенная масса молекулы), находящейся на расстоянии от центра сферической системы координат (рис. 2.3).

Решение уравнения (2.9) можно представить в виде произведения двух функций (  = f()j(), где функции f и j зависят только от одной переменной. Учет граничных условий приводит к тому, что значение энергии E_вр принимает только дискретные собственные значения:

, (2.11)

где J – вращательное квантовое число, принимающее значение J = 0, 1, 2, 3, …

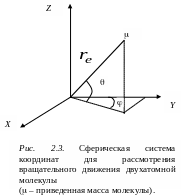
Выражение для энергии вращательных состояний молекулы можно получить гораздо проще, не решая уравнения Шрёдингера, а приняв во внимание только квантование момента вращения .

Согласно законам квантовой механики для свободной системы (в нашем случае двухатомной молекулы) квантуется квадрат момента количества движения. Он принимает ряд дискретных значений, определяемых формулой

, (2.12)

где J – вращательное квантовое число, принимающее целые значения (J = 0,1, 2, 3, …).

Одновременно квантуется и проекция вращательного момента количества движения на выделенное направление относительно неподвижной (лабораторной) системы координат. Эту систему координат будем обозначать X, Y, Z в отличие от системы координат X, Y, Z, cвязанной с молекулой. Проекция момента вращения относительно неподвижной оси (скажем, оси Z) равна:

, (2.13)

где m_J = J, J – 1, …, 0,…, –J принимает 2J + 1 значений. Энергия вращающейся молекулы не зависит от проекции момента количества движения, а только от величины квадрата момента, т. е.

(2.14)

Здесь учтено, что P = I.

Так как энергия молекулы не зависит от проекции момента количества движения, а только от квадрата момента, то говорят, что вращательные уровни анергии свободной молекулы всегда вырождены со степенью вырождения g = 2J + 1 (кроме уровня J = 0, для которого g = 1). Это связано с произвольностью ориентации момента количества движения относительно неподвижной системы координат.

Принимая во внимание выражение (2.12) для квадрата момента количества движения, равенство (2.14) можно переписать следующим образом:

, (2.15)

где значение момента инерции относится к равновесному расстоянию между атомами (от латинского слова equilibrium – равновесие). Как видим, с учетом квантования квадрата момента количества движения, мы получили значение вращательной энергии, как и в (2.11). Согласно выражению (2.15) коэффициент при вращательном квантовом числе есть величина постоянная для данной молекулы. Обозначим этот коэффициент через , тогда формулу (2.15) можно переписать более просто:

, (2.16)

где – вращательная постоянная, относящаяся к минимуму кривой потенциальной энергии и соответствующая равновесному расстоянию между атомами. Эта постоянная полностью определяет значение вращательной энергии двухатомной молекулы. При изучении оптических спектров вращательную постоянную обычно выражают в см^–1 (в системе СИ она, как и энергия, выражается в Дж). Оценим для молекул H₂ и HCl величину в Дж и в см^–1. для чего будем использовать ряд фундаментальных постоянных h = 6,626·10^–34Дж·с; с= 2,998·10⁸ м/с; I а.е.м. = 1,66·10^–27 кг; Н=1,67310^–27 кг; Сl³⁵=58,110^–27 кг; r_e^H₂ = 0,074 нм; r_e^HCl = 0,1275 нм.

Вычислим моменты инерции I_e:

Вычислим в Дж:

.

Учитывая, что величина постоянна и равна в системе СИ 5,5610^–69(Дж)²с², то выражение для будет иметь более простой вид:

Вычислим в см^–1 (так как , то для выражения в см^–1 необходимо полученные величины выражать в системе СИ за исключением постоянной с, которую следует выражать в смс^–1). Итак, получим:

.

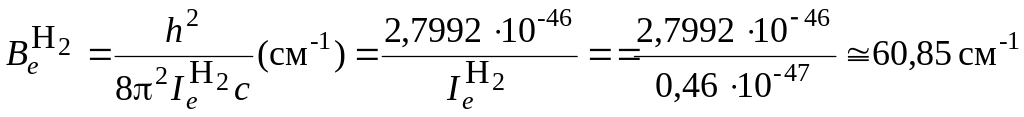
Из оценки вращательной постоянной видно, что чисто вращательные спектры располагаются в далекой ИК-области, соответствующей сантиметровому и миллиметровому диапазонам.

Так как значения вращательной энергии квадратично зависят от вращательного квантового числа J, то уровни вращательной энергии представляют собой расходящуюся последовательность.

В табл. 2.1 приведены значения Е_вр в зависимости от вращательного квантового числа J, а в табл. 2.2 межъядерные расстояния двухатомных молекул. Чтобы описать спектр поглощения или испускания, необходимо знать вероятности переходов между уровнями энергии и правила отбора.

Таблица 2.1