§ 50 Аналогії між кінематикою і статикою

Одним з основних понять статики є поняття сили. Сила в статиці твердого тіла (див. § 6) є ковзним вектором. Іншим важливим поняттям статики є поняття про момент пари сил. Момент пари сил (див. § 17) є вільним вектором. Аналогічні вектори є і в кінематиці. Вектор кутової швидкості (див. § 43.4) є ковзним вектором. Вектор моменту пари обертань (див. § 49.4) є вільним вектором.

Отже, між векторами і , і є аналогія. Треба зауважити, що ця аналогія є зовнішньою (формальною), а не фізичною. Проте знання її необхідне для більш глибокого розуміння законів механічного руху і є ще одним підтвердженням взаємозв’язку цих законів. Оскільки дані вектори лежать в основі побудови теоретичного курсу статики твердого тіла і кінематики, то природно чекати, що і між теоремами цих розділів є також відповідна аналогія. Очевидно, аналогії треба шукати між теоремами, які мають голов-ним чином геометричний зміст і доведення яких базується на загальних властивостях ковзних і вільних векторів. Систематизація теорем дає таку картину аналогії.

№	Статика	Кінематика
1	Аксіома про паралело- грам сил (§ 6)	Складання обертань твердого тіла навколо двох осей, що перетинаються (§ 49.3)
2	Зведення збіжної системи сил до канонічного вигляду (§ 7)	Складання обертань твердого тіла навколо осей, що перетинаються в одній точці (§ 49.3)
3	Пара сил і її властивості (§ 16)	Пара обертань і її властивості (§ 49.4)
4	Лема про паралельний перенос сили (§ 19)	Теорема про паралельний перенос вектора кутової швидкості
5	Зведення довільної системи сил до канонічного вигляду (§ 20)	Теорема про складання поступальних і обертальних рухів
6	Складання паралельних сил (курс фізики середньої школи, додаток 4)	Складання обертань тіла навколо паралельних осей (§ 49.4)

Як видно з таблиці, більшість з наведених теорем доведена вище. Під номерами 4 і 5 вказані нові, ще не доведені, теореми кінематики твердого тіла. Доведемо ці теореми в даному параграфі.

Теорему про паралельний перенос вектора кутової швидкості сформулюємо за аналогією леми про паралельний перенос сили:

не змінюючи миттєвого розподілу швидкостей в тілі, вектор кутової швидкості можна паралельно перенести в будь-яку точку, якщо при цьому приєднати пару обертань, момент якої геометрично дорівнює моменту заданої кутової швидкості відносно точки переносу.

Доведення даної теореми є по суті повторенням доведення аналогічної теореми статики. Нехай деяке тверде тіло (рис. 157, а) обертається навколо осі з кутовою швидкістю . В точці до тіла вздовж осі , яка паралельна осі , приєднаємо еквівалентну нулеві сукупність обертань так, що (рис. 157, б). Вектори і утворюють пару обертань, яку за формулою (2.109) замінено вільним вектором-моментом пари обертань

.

Рис. 157

В результаті в точці (рис. 157, в) залишаться вектори і , які надаватимуть точкам тіла такі ж миттєві швидкості як і вектор , що був прикладений в точці .

Отже, якщо при паралельному переносі вектора кутової швидкості в довільну точку приєднується пара обертань, момент якої геометрично рівний моменту заданої кутової швидкості відносно точки переносу, то розподіл миттєвих швидкостей в тілі не зміниться.

Отриману теорему використаємо для доведення теореми, яка за доведенням і змістом формально подібна (аналогічна) зведенню довільної системи сил до канонічного вигляду.

Теорема

Сукупність одночасних “n” поступальних рухів, швидкості яких , , ..., і “m” миттєвих обертальних рухів з кутовими швидкостями , , ..., твердого тіла, еквівалентна сукупності одного поступального і одного обертального рухів. Кутова швидкість результуючого обертання дорівнює геометричній сумі (головному вектору) кутових швидкостей складових обертань

, (2.110)

а швидкість результуючого поступального руху дорівнює геометричній сумі моментів кутових швидкостей відносно центра зведення і швидкостей поступальних рухів

. (2.111)

Оскільки кожний поступальний рух можна представити відповідною парою обертань, то геометрична сума (2.111) є не що інше, як головний момент кутових швидкостей відносно центра зведення.

Доведення сформульованої теореми з врахуванням наведених аналогій між статикою і кінематикою є дуже простим. Розглянемо тіло, яке одночасно здійснює поступальних рухів з швидкостями , , ..., і миттєвих обертальних рухів з кутовими швидкостями , , ..., (рис. 158, а). Виберемо точку центром зведення. Враховуючи, що вектори кутових швидкостей є ковзними векторами і, користуючись правилом їх паралельного переносу (див. попередню теорему), переносимо їх до центра . В результаті такої дії отримаємо сукупність векторів кутових швидкостей ( , , ..., ), прикладених до точки і пар обертань, моменти яких визначають відповідні поступальні рухи

, , ..., . (а)

За правилом складання обертань навколо осей, що перетинаються, зведемо обертання з кутовими швидкостями , , ..., , які тепер прикладені до однієї точки , до одного обертання з кутовою швидкістю, яка дорівнює геометричній сумі заданих кутових швидкостей

. (б)

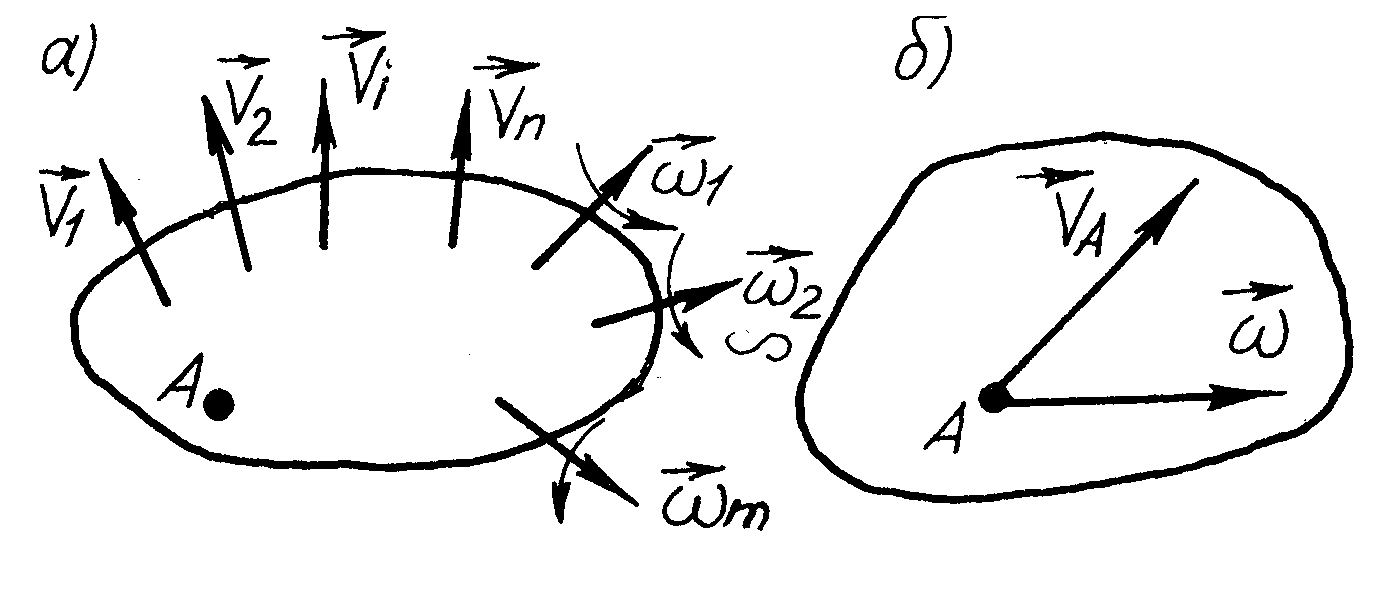
Рис. 158

Вектори швидкостей поступальних рухів , , ..., є вільними векторами, то, паралельно перенісши їх до точки і геометрично склавши, отримаємо

.

Склавши отриману швидкість з швидкостями , , ..., знайдемо швидкість результуючого поступального руху

.

Враховуючи (а), матимемо

або

. (в)

Отримані результати і рівності (б) і (в) підтверджують сформульовану теорему, отже вона доведена.

Розвиваючи далі аналогію між статикою і кінематикою, можна показати (читачу пропонується це проробити самостійно), що:

1. В кінематиці, як і в статиці, є два інваріанти, тобто дві величини, які не залежать від вибору центра зведення рухів. Першим інваріантом є головний вектор обертання, який визначається за формулою (2.110). Другим інваріантом є скаляр-ний добуток головного вектора обертання (формула 2.110) на головний момент (вектора швидкості результуючого поступального руху, формула (2.111)).

2. Якщо результуюча швидкість поступального руху (головний момент) дорівнює нулеві, то рух тіла, який складається з обертальних рухів і поступальних рухів, зведеться до одного обертального руху, кутова швидкість якого визначається за формулою (2.110).

3. Якщо кутова швидкість результуючого обертання (головний вектор обертання) дорівнює нулеві, то рух тіла, який складається з обертальних рухів і поступальних рухів, зведеться до одного поступального руху, швидкість якого визначатиметься за формулою (2.111).

4. За умови , , результуючим рухом тіла буде обертальний рух навколо осі, що буде зміщена від центра зведення на відстань .

5. Якщо вектор , і вони не є взаємно перпендикулярними, тобто їх скалярний добуток , відмінний від нуля, то вся система рухів твердого тіла зведеться до кінематичного гвинта.

Все перераховане аналогічне частковим випадкам зведення довільної системи сил до заданого центра (§ 21).

Д О Д А Т К И