
- •Рецензенти:
- •76019, Івано-Франківськ, вул. Карпатська, 15 Івано-Франківський національний технічний університет нафти і газу
- •§ 2 Основні поняття теоретичної механіки
- •1 Статика твердого тіла
- •§ 3 Предмет статики твердого тіла
- •§ 4 Основні поняття статики
- •§ 5 В’язі та їх реакції
- •§ 6 Вихідні положення (аксіоми) статики
- •1. Аксіома зрівноваження двох сил.
- •2. Аксіома приєднання і виключення зрівноваженої системи сил.
- •3. Аксіома дії і протидії (ііі-ій закон Ньютона).
- •4. Аксіома накладання додаткових в’язей.
- •5. Аксіома паралелограма.
- •1.1 Система збіжних сил
- •§ 7 Зведення системи збіжних сил до канонічного вигляду
- •1. Геометричний спосіб визначення рівнодійної.
- •2. Аналітичний спосіб визначення рівнодійної.
- •§ 8 Умови і рівняння рівноваги системи збіжних сил
- •1. Геометрична умова рівноваги.
- •2. Аналітичні умови рівноваги. Рівняння рівноваги.
- •§ 9 Алгоритм розв’язання задач на рівновагу
- •Питання для самоконтролю
- •1.2 Теорія моменту сил
- •§ 10 Момент сили відносно точки
- •§ 11 Момент сили відносно осі
- •§ 12 Залежність між моментом сили відносно точки і моментом сили відносно осі, яка проходить через цю точку
- •§ 13 Аналітичне визначення моменту сили відносно довільної точки
- •§ 14 Теорема Варіньйона
- •Питання для самоконтролю
- •1.3 Довільна система сил
- •§ 15 Головний вектор і головний момент системи сил
- •1. Геометричний спосіб
- •2. Аналітичний спосіб
- •§ 16 Пара сил і її момент
- •§ 17 Еквівалентність пар сил
- •§ 18 Додавання пар сил
- •§ 19 Лема про паралельний перенос сили
- •§ 20 Зведення довільної системи сил до заданого центра
- •§ 21 Окремі випадки зведення довільної системи сил
- •§ 22 Інваріанти довільної системи сил
- •§ 23 Аналітичні умови рівноваги просторової системи сил
- •§ 24 Аналітичні умови рівноваги плоскої системи сил
- •§ 25 Статично означені і статично неозначені задачі
- •§ 26 Рівновага системи тіл
- •Питання для самоконтролю
- •1.4 Деякі спеціальні питання статики
- •§ 27 Тертя ковзання
- •§ 28 Конус тертя. Область рівноваги
- •§ 29 Тертя кочення
- •§ 30 Поняття про ферми
- •Питання для самоконтролю
- •1.5 Система паралельних сил. Центр ваги твердого тіла
- •§ 31 Зведення системи паралельних сил до канонічного вигляду
- •§ 32 Центр ваги твердого тіла
- •1. Центр ваги однорідного тіла (центр ваги об’єму)
- •2. Центр ваги площі однорідного плоского тіла (центр ваги площі)
- •3. Центр ваги однорідного лінійного тіла (центр ваги лінії)
- •§ 33 Центр ваги деяких простих геометричних фігур
- •§ 34 Способи визначення положення центра ваги тіла
- •Питання для самоконтролю
- •2 Кінематика
- •§ 35 Предмет кінематики
- •2.1 Кінематика точки
- •§ 36 Векторний спосіб вивчення руху точки
- •§ 37 Координатний спосіб вивчення руху точки
- •§ 38 Швидкість і пришвидшення точки в полярних координатах
- •§ 39 Натуральна система координат
- •§ 40 Натуральний спосіб вивчення руху точки
- •§ 41 Класифікація руху точки за її пришвидшеннями
- •Питання для самоконтролю
- •2.2 Кінематика твердого тіла
- •§ 42 Поступальний рух твердого тіла
- •§ 43 Обертання твердого тіла навколо нерухомої осі
- •§ 43.1 Рівняння обертання тіла навколо нерухомої осі
- •§ 43.2 Рівняння рівномірного і рівнозмінного обертання
- •§ 43.3 Швидкість і пришвидшення точки тіла, яке обертається навколо нерухомої осі
- •§ 43.4 Вектор кутової швидкості
- •§ 43.5 Векторні вирази швидкості, доцентрового і обертального пришвидшень точки тіла при обертальному русі
- •Питання для самоконтролю
- •2.1 Кінематика складного руху точки
- •§ 44 Складний рух точки
- •§ 44.1 Основні поняття і визначення
- •§ 44.2 Теорема про складання швидкостей
- •§ 44.3 Теорема про складання пришвидшень (Теорема Коріоліса)
- •§ 44.4 Коріолісове пришвидшення і його визначення
- •Питання для самоконтролю
- •2.4 Кінематика складного руху твердого тіла
- •§ 45 Складний рух твердого тіла
- •§ 46 Плоскопаралельний (плоский) рух твердого тіла
- •§ 46.1 Основні поняття і визначення
- •§ 46.2 Рівняння руху плоскої фігури
- •§ 46.3 Рівняння руху точки плоскої фігури
- •§ 46.4 Теорема про швидкості точок плоскої фігури та її наслідок
- •§ 46.5 Миттєвий центр швидкостей
- •§ 46.6 Способи визначення положення миттєвого центра швидкостей
- •§ 46.7 Теорема про пришвидшення точок плоскої фігури
- •§ 46.8 Миттєвий центр пришвидшень
- •Питання для самоконтролю
- •§ 47 Обертання твердого тіла навколо нерухомої точки
- •§ 47.1 Кути Ейлера. Рівняння обертання твердого тіла навколо нерухомої точки
- •§ 47.2 Теорема Ейлера-Даламбера
- •§ 47.3 Кутова швидкість і кутове пришвидшення тіла, що обертається навколо нерухомої точки
- •§ 47.4 Швидкість точок твердого тіла, яке обертається навколо нерухомої точки
- •§ 47.5 Пришвидшення точок твердого тіла, яке обертається навколо нерухомої точки
- •Питання для самоконтролю
- •§ 48 Рух вільного твердого тіла
- •Питання для самоконтролю
- •§ 49 Синтез рухів
- •§ 49.1 Складання поступальних рухів твердого тіла
- •§ 49.2 Складання поступального і обертального рухів твердого тіла
- •§ 49.3 Складання обертань навколо осей, що перетинаються
- •§ 49.4 Складання обертань навколо паралельних осей
- •Питання для самоконтролю
- •§ 50 Аналогії між кінематикою і статикою
- •1 Проекція вектора на площину
- •2 Проекція вектора на вісь
- •3 Приклади розв’язування задач на рівновагу тіла
- •4 Додавання двох паралельних сил
- •5 Доведення теореми про еквівалентність пар сил
- •6 Найменше значення головного моменту системи сил
- •Список використаної літератури, деяких підручників і навчальних посібників з теоретичної механіки
- •Предметний покажчик
§ 43 Обертання твердого тіла навколо нерухомої осі
Р
Рис. 98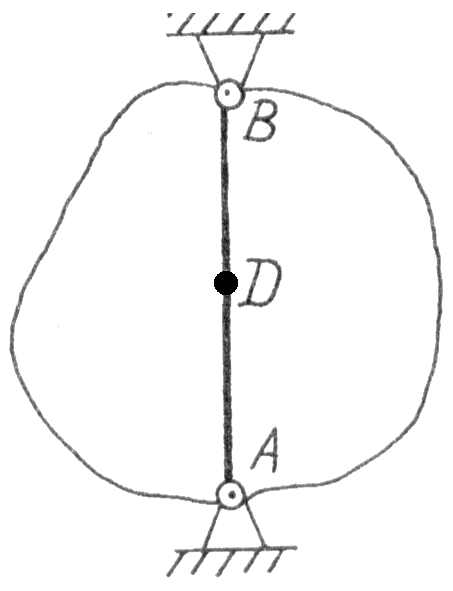
![]() (рис. 98).
(рис. 98).
Тоді з формули (2.31)
![]()
отримуємо,
що
![]() тобто
тобто
![]() .
.
Виберемо
тепер на прямій
довільну точку
,
для якої вектор
![]() ,
де
– деяке число. За формулою (2.31) визначимо
швидкість точки
,
де
– деяке число. За формулою (2.31) визначимо
швидкість точки
![]() ,
або
,
або
![]()
Оскільки
![]() ,
,
![]() – число, то отримуємо, що
– число, то отримуємо, що
![]() .
Точка
на прямій
вибрана довільно, а це означає, що пряма
є геометричне місце точок, швидкості
яких дорівнюють нулеві, тобто є віссю
обертання.
.
Точка
на прямій
вибрана довільно, а це означає, що пряма
є геометричне місце точок, швидкості
яких дорівнюють нулеві, тобто є віссю
обертання.
Отже,
обертанням твердого тіла навколо нерухомої осі називається такий його рух, при якому хоча б дві точки тіла є нерухомими.
В
Рис. 99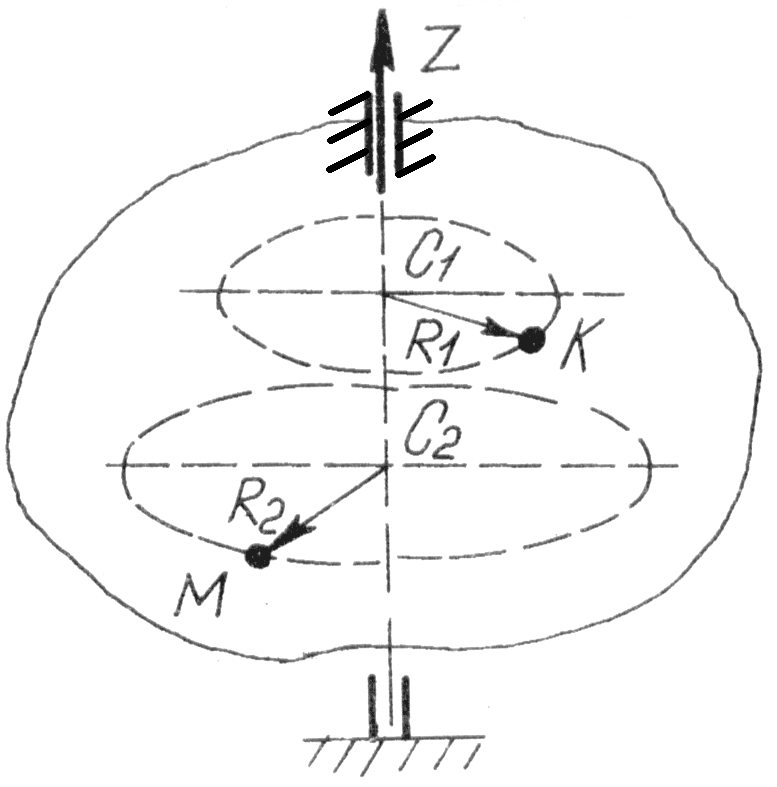
![]() Точки тіла, які не належать осі обертання
(наприклад, точка
і
(рис. 99), очевидно, рухатимуться по колах,
площини яких перпендикулярні до осі
обертання, а центри їх знаходяться на
осі обертання. Радіуси цих кіл
Точки тіла, які не належать осі обертання
(наприклад, точка
і
(рис. 99), очевидно, рухатимуться по колах,
площини яких перпендикулярні до осі
обертання, а центри їх знаходяться на
осі обертання. Радіуси цих кіл
![]() і
і
![]() визначають відстані відповідних точок
до осі обертання.
визначають відстані відповідних точок
до осі обертання.
§ 43.1 Рівняння обертання тіла навколо нерухомої осі
Розглянемо
тверде тіло, яке обертається навколо
нерухомої осі (рис. 100). Для визначення
положення тіла через вісь обертання
проведемо дві півплощини: нерухому
і рухому
,
яка жорстко з’єднана з тілом, тобто
положення і рух її в
Рис. 100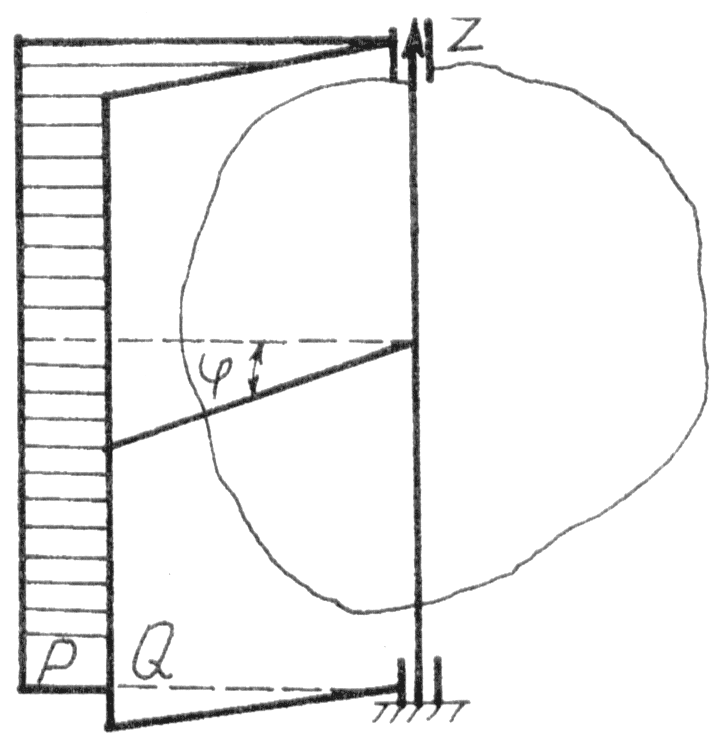
![]() (2.34)
(2.34)
Записане рівняння називається рівнянням (законом) обертання твердого тіла навколо нерухомої осі, бо, знаючи це рівняння, можна визначати положення тіла в будь-який момент часу.
Кут повороту вимірюється в радіанах і вважається додатним, якщо він відкладається проти ходу годинникової стрілки, коли дивитися з кінця осі обертання.
Перша похідна за часом від кута повороту називається алгебраїчною кутовою швидкістю.
Вона
позначається буквою
![]() (омега)
(омега)
![]() (2.35)
(2.35)
Перша похідна за часом від алгебраїчної кутової швид-кості називається алгебраїчним кутовим пришвидшенням.
Кутове
пришвидшення позначається буквою
![]() (епсилон).
(епсилон).
![]() (2.36)
(2.36)
Модулі
алгебраїчної кутової швидкості і
кутового пришвидшення позначаються
![]() ,
,
![]() і будемо називати їх просто кутовою
швидкістю
і кутовим
пришвид-шенням.
На рисунках алгебраїчну кутову швидкість
і кутове пришвидшення
показують дуговими стрілками, додатний
напрям
яких вибирають проти ходу годинникової
стрілки, якщо дивитись з кінця осі
обертання.
і будемо називати їх просто кутовою
швидкістю
і кутовим
пришвид-шенням.
На рисунках алгебраїчну кутову швидкість
і кутове пришвидшення
показують дуговими стрілками, додатний
напрям
яких вибирають проти ходу годинникової
стрілки, якщо дивитись з кінця осі
обертання.
Кут повороту , кутова швидкість і кутове пришвид-шення є кінематичними характеристиками обертання твердого тіла навколо нерухомої осі.
З’ясуємо одиниці вимірювання цих величин. В теоретичній механіці, як і у фізиці та в більшості інших дисциплін, кут повороту найчастіше вимірюється в радіанах (рад), тобто:
![]()
Тоді згідно з формулою (2.35) кутова швидкість буде вимірюватись в рад/с, тобто:
![]()
а кутове пришвидшення
![]()
У
техніці кут повороту тіла визначають
в обертах. Кількість обертів найчастіше
позначають буквою
![]() .
Оскільки за один оберт тіло повертається
на
.
Оскільки за один оберт тіло повертається
на
![]() радіан, то за
обертів воно повертається на кут
радіан, то за
обертів воно повертається на кут
![]() рад.
(2.37)
рад.
(2.37)
Кутову
швидкість у техніці часто характеризують
числом обертів за хвилину (об/хв) і
позначають буквою
.
В паспортах кожного двигуна внутрішнього
згоряння, електродвигуна вказане
експлуатаційне число обертів за хвилину.
Зв’язок між
![]() і
визначається формулою
і
визначається формулою
![]()
тобто
![]() (2.38)
(2.38)
Залежність (2.38) – це формула переходу від кутової швидкості в обертах за хвилину до кутової швидкості в радіанах за секунду. Цю формулу бажано запам’ятати, бо вона часто застосовується в реальних розрахунках і не треба її плутати з формулою
![]() ,
(2.39)
,
(2.39)
де
![]() – частота обертання тіла, тобто кількість
обертів тіла за одну секунду, яка також
часто зустрічається в технічній
літературі.
– частота обертання тіла, тобто кількість
обертів тіла за одну секунду, яка також
часто зустрічається в технічній
літературі.
