§ 40 Натуральний спосіб вивчення руху точки

В даному способі задання руху точки на відміну від попередніх вказується траєкторія, по якій рухається точка. Припустимо, що точка рухається по деякій траєкторії (рис. 92). На заданій траєкторії вибираємо деяку нерухому точку , відносно якої будемо визначати положення рухомої точки . Саме положення точки визначається дугою , яка найчастіше позначається буквою і називається дуговою координатою. Отже, нерухома точка є початком відліку дугової координати. В один бік відліку дугова координата вважається додатною, в протилежний бік – від’ємною. Вибір додатного напряму відліку дугової координати є довільним.

П

Рис. 92

ри русі точки її дугова координата неперервно змінюється з часом, тобто є функцією часу

(2.17)

Записане рівняння, яке дає змогу визначити положення рухомої точки на траєкторії в будь-який момент часу, називається рівнянням (законом) руху точки по траєкторії. Очевидно, як і попередніх випадках, функція повинна бути однозначною і неперервною разом із своїми похідними.

Тут треба зауважити, що дугова координата точки і шлях, пройдений точкою, який також часто позначається буквою , в загальному випадку відрізняються. І дійсно, якщо припустити, що за проміжок часу точка переміститься з положення в положення і повернеться в положення (рис. 92), то в момент часу дугова координата точки буде , а шлях, пройдений точкою (позначимо його буквою ), буде дорівнювати сумі довжин двох дуг: . До того ж дугова координата точки може бути як додатною, так і від’ємною, а шлях, який проходить точка, є завжди додатним.

Швидкість точки визначимо за формулою (2.2)

(а)

Оскільки кожному значенню координати відповідає певне значення радіуса-вектора (див. рис. 92), то можна вважати, що радіус-вектор є неперервною функцією , і формулу (а) можна записати так:

(б)

(Відомості з математики. В математиці похідна позначається вектором і доводиться, що величина вектора дорівнює одиниці, і цей вектор напрямлений по дотичній до лінії в бік зростання дугової координати, тобто вектор є ортом дотичної. Отже, , де – орт дотичної).

Враховуючи це, формула (б) набуває вигляду

(2.18)

Формула (2.18) визначає вектор швидкості точки у випадку, коли рух її задано натуральним способом, тобто відома траєкторія точки і закон її руху по траєкторії (рівн. 2.17).

Аналізуючи отриману формулу, можна зробити такі висновки:

1. Якщо то вектор швидкості співпадає з напрямом вектора . Якщо , то вектор швидкості протилежний до напряму вектора (рис. 93). В першому і другому випадках вектор швидкості буде дотичним до траєкторії.

Рис. 93

Отже, вектор швидкості точки в кожному її положенні є дотичним до траєкторії.

2. Вектор швидкості дорівнює добутку одиничного вектора на вираз . Згідно з поняттями векторної алгебри цей вираз визначає проекцію вектора швидкості на дотичну вісь і називається алгебраїчною швидкістю точки, тобто

(2.19)

Алгебраїчна швидкість точки дорівнює першій похідній за часом від дугової координати.

Величина (модуль) швидкості при натуральному способі задання руху дорівнює

Оскільки пришвидшення точки – це перша похідна за ча-сом від її вектора швидкості, то в нашому випадку отримаємо

Вектор є змінним вектором, бо при русі точки змінюється його напрям. Отже, похідну треба брати від добутку.

(а)

Якщо врахувати, що орт змінює свій напрям при зміні дугової координати , тобто він є функцією дугової координати то

і співвідношення (в) набуває вигляду

(г)

(Відомості з математики. В математиці похідна позначається вектором , який називається вектором кривизни. Вектор кривизни напрямляється по напряму головної нормалі і дорівнює , де – радіус кривизни лінії. Отже,

.

Враховуючи це і формулу (2.19), отримуємо, що

(2.20)

Пришвидшення точки дорівнює геометричній сумі двох доданків.

Векторна складова напрямлена по головній нормалі, на що вказує вектор – орт головної нормалі, познача-ється і називається вектором нормального пришвидшення

(2.21)

Скалярний співмножник при орті , очевидно, визначає проекцію нормального пришвидшення на головну нормаль

(2.22)

Векторна складова , яка напрямлена по дотичній, на що вказує вектор – орт дотичної, позначається і назива-ється вектором тангенціального (дотичного) пришвидшення

(2.23)

Скалярний співмножник при орті , очевидно, визначає проекцію тангенціального пришвидшення на дотичну вісь

(2.24)

Нормальне пришвидшення характеризує зміну вектора швидкості за напрямом. Величина цього пришвидшення визначається за формулою (2.22), а його вектор завжди напрямлений по головній нормалі в бік вгнутості траєкторії (рис. 94).

Дотичне пришвидшення характеризує зміну вектора швидкості за величиною. Алгебраїчна величина цього пришвидшення визначається за формулою (2.24), а його вектор напрямлений по вектору при і в протилежний бік при (рис. 94).

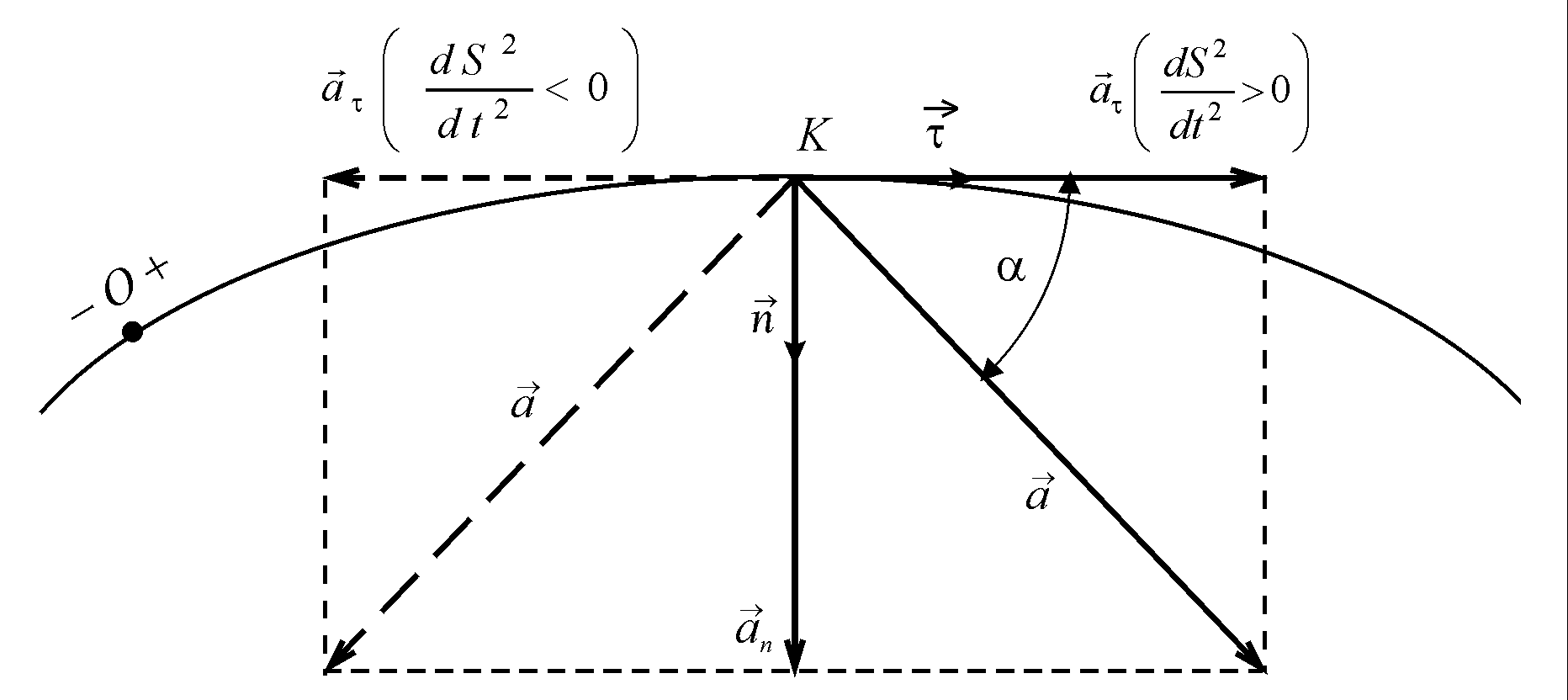
Рис. 94

Підставляючи формули (2.21), (2.23) в (2.20), отримаємо

. (2.25)

Пришвидшення точки дорівнює геометричній сумі її нормального і тангенціального пришвидшень.

Оскільки орти і взаємно перпендикулярні, то вектор нормального пришвидшення , буде перпендикулярним до вектора тангенціального пришвидшення , і модуль повного пришвидшення буде визначатися за теоремою Піфагора

. (2.26)

Формули (2.21)-(2.26) визначають вектор пришвидшення точки у випадку, коли рух її задано натуральним способом, тобто відома траєкторія, по якій рухається точка і закон її руху по траєкторії (рів. 2.17).

З рис. 94 можна зробити такі висновки:

1. Вектор пришвидшення точки знаходиться в стичній площині.

2. Проекція вектора пришвидшення точки на бінормаль завжди дорівнює нулеві, тобто

3. Кут, який утворює вектор пришвидшення точки з дотичною до траєкторії, можна визначити з формули

. (2.27)