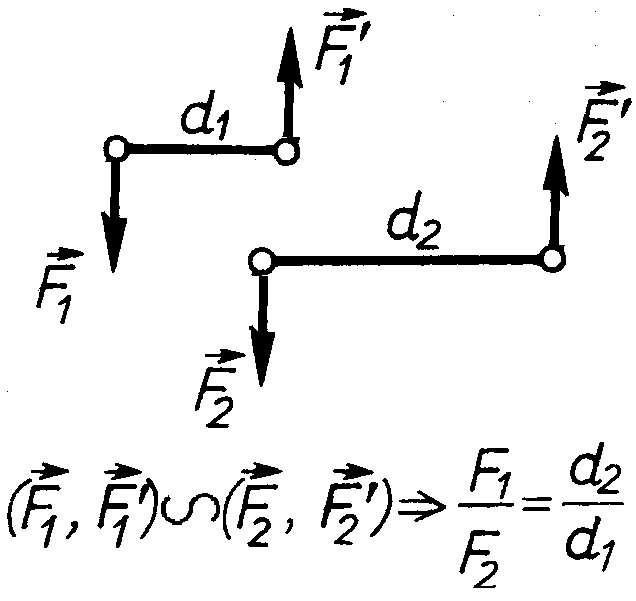- •Рецензенти:
- •76019, Івано-Франківськ, вул. Карпатська, 15 Івано-Франківський національний технічний університет нафти і газу
- •§ 2 Основні поняття теоретичної механіки
- •1 Статика твердого тіла
- •§ 3 Предмет статики твердого тіла
- •§ 4 Основні поняття статики
- •§ 5 В’язі та їх реакції
- •§ 6 Вихідні положення (аксіоми) статики
- •1. Аксіома зрівноваження двох сил.
- •2. Аксіома приєднання і виключення зрівноваженої системи сил.
- •3. Аксіома дії і протидії (ііі-ій закон Ньютона).
- •4. Аксіома накладання додаткових в’язей.
- •5. Аксіома паралелограма.
- •1.1 Система збіжних сил
- •§ 7 Зведення системи збіжних сил до канонічного вигляду
- •1. Геометричний спосіб визначення рівнодійної.
- •2. Аналітичний спосіб визначення рівнодійної.
- •§ 8 Умови і рівняння рівноваги системи збіжних сил
- •1. Геометрична умова рівноваги.
- •2. Аналітичні умови рівноваги. Рівняння рівноваги.
- •§ 9 Алгоритм розв’язання задач на рівновагу
- •Питання для самоконтролю
- •1.2 Теорія моменту сил
- •§ 10 Момент сили відносно точки
- •§ 11 Момент сили відносно осі
- •§ 12 Залежність між моментом сили відносно точки і моментом сили відносно осі, яка проходить через цю точку
- •§ 13 Аналітичне визначення моменту сили відносно довільної точки
- •§ 14 Теорема Варіньйона
- •Питання для самоконтролю
- •1.3 Довільна система сил
- •§ 15 Головний вектор і головний момент системи сил
- •1. Геометричний спосіб
- •2. Аналітичний спосіб
- •§ 16 Пара сил і її момент
- •§ 17 Еквівалентність пар сил
- •§ 18 Додавання пар сил
- •§ 19 Лема про паралельний перенос сили
- •§ 20 Зведення довільної системи сил до заданого центра
- •§ 21 Окремі випадки зведення довільної системи сил
- •§ 22 Інваріанти довільної системи сил
- •§ 23 Аналітичні умови рівноваги просторової системи сил
- •§ 24 Аналітичні умови рівноваги плоскої системи сил
- •§ 25 Статично означені і статично неозначені задачі
- •§ 26 Рівновага системи тіл
- •Питання для самоконтролю
- •1.4 Деякі спеціальні питання статики
- •§ 27 Тертя ковзання
- •§ 28 Конус тертя. Область рівноваги
- •§ 29 Тертя кочення
- •§ 30 Поняття про ферми
- •Питання для самоконтролю
- •1.5 Система паралельних сил. Центр ваги твердого тіла
- •§ 31 Зведення системи паралельних сил до канонічного вигляду
- •§ 32 Центр ваги твердого тіла
- •1. Центр ваги однорідного тіла (центр ваги об’єму)
- •2. Центр ваги площі однорідного плоского тіла (центр ваги площі)
- •3. Центр ваги однорідного лінійного тіла (центр ваги лінії)
- •§ 33 Центр ваги деяких простих геометричних фігур
- •§ 34 Способи визначення положення центра ваги тіла
- •Питання для самоконтролю
- •2 Кінематика
- •§ 35 Предмет кінематики
- •2.1 Кінематика точки
- •§ 36 Векторний спосіб вивчення руху точки
- •§ 37 Координатний спосіб вивчення руху точки
- •§ 38 Швидкість і пришвидшення точки в полярних координатах
- •§ 39 Натуральна система координат
- •§ 40 Натуральний спосіб вивчення руху точки
- •§ 41 Класифікація руху точки за її пришвидшеннями
- •Питання для самоконтролю
- •2.2 Кінематика твердого тіла
- •§ 42 Поступальний рух твердого тіла
- •§ 43 Обертання твердого тіла навколо нерухомої осі
- •§ 43.1 Рівняння обертання тіла навколо нерухомої осі
- •§ 43.2 Рівняння рівномірного і рівнозмінного обертання
- •§ 43.3 Швидкість і пришвидшення точки тіла, яке обертається навколо нерухомої осі
- •§ 43.4 Вектор кутової швидкості
- •§ 43.5 Векторні вирази швидкості, доцентрового і обертального пришвидшень точки тіла при обертальному русі
- •Питання для самоконтролю
- •2.1 Кінематика складного руху точки
- •§ 44 Складний рух точки
- •§ 44.1 Основні поняття і визначення
- •§ 44.2 Теорема про складання швидкостей
- •§ 44.3 Теорема про складання пришвидшень (Теорема Коріоліса)
- •§ 44.4 Коріолісове пришвидшення і його визначення
- •Питання для самоконтролю
- •2.4 Кінематика складного руху твердого тіла
- •§ 45 Складний рух твердого тіла
- •§ 46 Плоскопаралельний (плоский) рух твердого тіла
- •§ 46.1 Основні поняття і визначення
- •§ 46.2 Рівняння руху плоскої фігури
- •§ 46.3 Рівняння руху точки плоскої фігури
- •§ 46.4 Теорема про швидкості точок плоскої фігури та її наслідок
- •§ 46.5 Миттєвий центр швидкостей
- •§ 46.6 Способи визначення положення миттєвого центра швидкостей
- •§ 46.7 Теорема про пришвидшення точок плоскої фігури
- •§ 46.8 Миттєвий центр пришвидшень
- •Питання для самоконтролю
- •§ 47 Обертання твердого тіла навколо нерухомої точки
- •§ 47.1 Кути Ейлера. Рівняння обертання твердого тіла навколо нерухомої точки
- •§ 47.2 Теорема Ейлера-Даламбера
- •§ 47.3 Кутова швидкість і кутове пришвидшення тіла, що обертається навколо нерухомої точки
- •§ 47.4 Швидкість точок твердого тіла, яке обертається навколо нерухомої точки
- •§ 47.5 Пришвидшення точок твердого тіла, яке обертається навколо нерухомої точки
- •Питання для самоконтролю
- •§ 48 Рух вільного твердого тіла
- •Питання для самоконтролю
- •§ 49 Синтез рухів
- •§ 49.1 Складання поступальних рухів твердого тіла
- •§ 49.2 Складання поступального і обертального рухів твердого тіла
- •§ 49.3 Складання обертань навколо осей, що перетинаються
- •§ 49.4 Складання обертань навколо паралельних осей
- •Питання для самоконтролю
- •§ 50 Аналогії між кінематикою і статикою
- •1 Проекція вектора на площину
- •2 Проекція вектора на вісь
- •3 Приклади розв’язування задач на рівновагу тіла
- •4 Додавання двох паралельних сил
- •5 Доведення теореми про еквівалентність пар сил
- •6 Найменше значення головного моменту системи сил
- •Список використаної літератури, деяких підручників і навчальних посібників з теоретичної механіки
- •Предметний покажчик
§ 16 Пара сил і її момент
Система
двох рівних за величиною протилежно
напря-млених
сил (![]() ),
лінії дії яких не співпадають, називається
парою
сил
(рис. 29).
),
лінії дії яких не співпадають, називається
парою
сил
(рис. 29).
Рис. 29 |
Рис. 30 |
Основними характеристиками пари сил є:
1.
Площина
дії пари сил
– це площина, в якій знаходиться пара
сил. На рис. 29, на якому зображено пару
сил
![]() ,
– це площина дії заданої пари сил. Вона
єдина, оскільки через дві паралельні
лінії можна провести тільки одну площину.
,
– це площина дії заданої пари сил. Вона
єдина, оскільки через дві паралельні
лінії можна провести тільки одну площину.
2.
Плече
пари сил
– це найкоротша відстань між лініями
дії сил пари. На рис. 29 воно позначено
літерою
![]() .
.
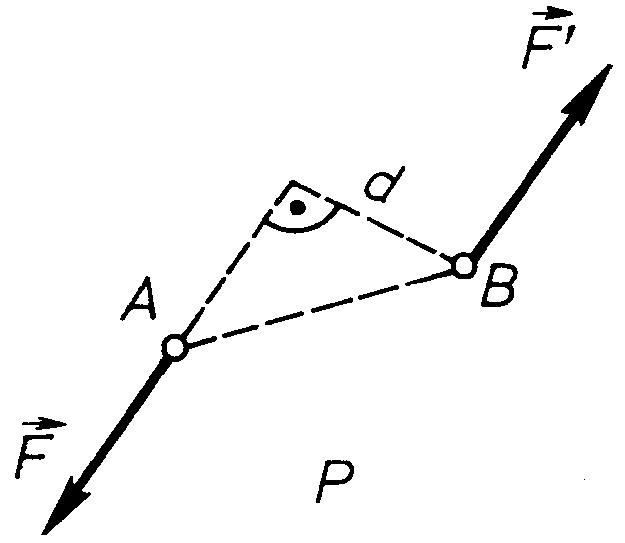
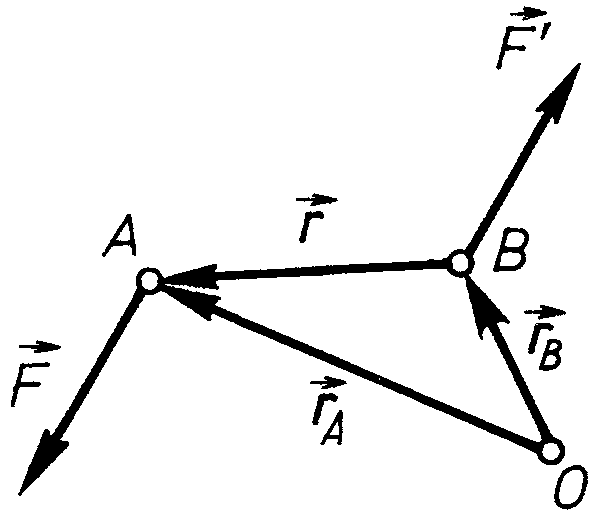
3. Момент пари сил.
Для
введення поняття моменту пари сил
розглянемо пару сил
,
сили якої прикладені в точках
і
(рис. 30). Виберемо довільну точку
і проведемо відповідні радіуси-вектори
![]() .
За формулою (1.26) визначимо головний
вектор пари сил
.
За формулою (1.26) визначимо головний
вектор пари сил
![]() .
.
Отже, головний вектор пари сил дорівнює нулеві.
За формулою (1.27) визначимо головний момент пари сил відносно довільної точки
![]() .
.
Оскільки , отримаємо
![]() ,
,
тобто:
![]() .
.
Головний момент пари сил не залежить від положення точки, відносно якої він визначається, а залежить тільки від параметрів самої пари сил і називається моментом пари сил.
Отже,
момент
пари сил
![]() дорівнює
векторному моменту однієї сили пари
відносно точки прикладання іншої сили
даної пари, тобто
дорівнює
векторному моменту однієї сили пари
відносно точки прикладання іншої сили
даної пари, тобто
![]() .
(1.34)
.
(1.34)
З отриманого випливає:
1. Момент пари сил – це вектор, бо вектором є момент сили відносно точки.
2.
Вектор моменту пари сил перпендикулярний
до площини дії пари, оскільки вектор
![]() перпендикулярний до площини, яка
проходить через точку
і вектор сили
,
а це є площина дії пари сил.
перпендикулярний до площини, яка
проходить через точку
і вектор сили
,
а це є площина дії пари сил.
3. Якщо побудувати вектор (рис. 31, а), а це згідно з формулою (1.34) буде вектор моменту пари сил, то ми отримаємо, що момент пари сил як вектор напрямлений в бік, звідки спостерігач бачить намагання пари сил повернути тіло проти руху годинникової стрілки.
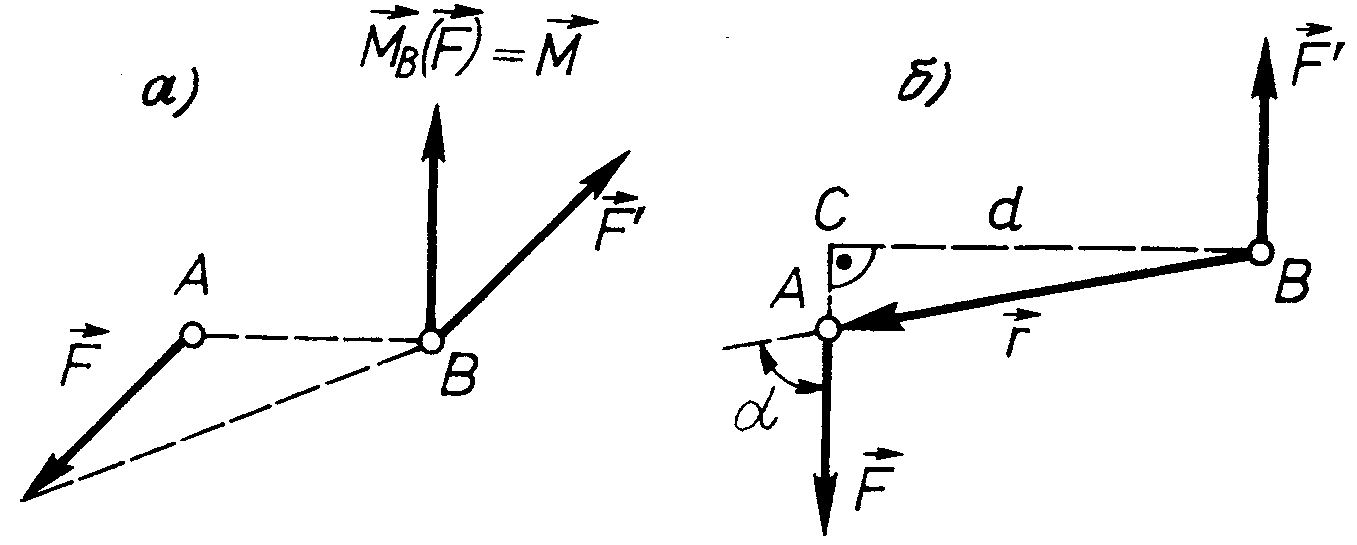
Рис. 31
Визначимо величину вектора моменту пари сил. За формулою (1.34) маємо
![]() .
.
Оскільки (див. рис. 31, б)
![]() ,
,
отримуємо
![]() .
(а)
.
(а)
Отже,
момент пари сил чисельно дорівнює добутку модуля однієї сили пари на її плече.
Якщо пари сил розміщені в одній площині, то величини їх моментів знаходяться за формулою (a), а вектори цих моментів будуть колінеарними. В цьому випадку доцільніше користуватися не векторним поняттям моменту пари сил, а алгебраїчним.
Алгебраїчний момент пари сил дорівнює добутку, взятому з відповідним знаком, модуля однієї сили пари на її плече, тобто
![]() .
(1.35)
.
(1.35)
Той чи інший знак у цій формулі визначається за таким правилом: якщо спостерігач бачить намагання пари сил повернути тіло проти годинникової стрілки, береться знак “+”, в противному разі – знак “–“.
Алгебраїчні моменти пари сил на рисунках показують дуговими стрілками (рис. 32).
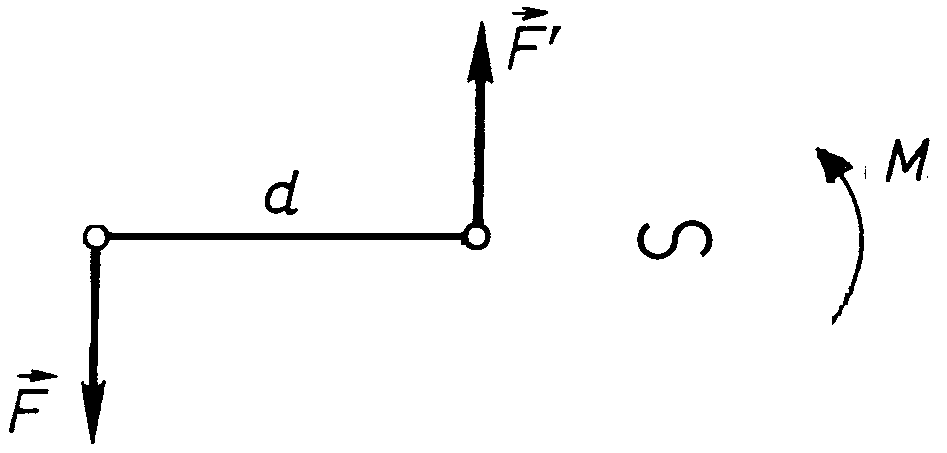
Рис. 32
Зазначимо, що одиницею виміру моменту пари сил, як і моменту сили, є Нм.
§ 17 Еквівалентність пар сил
Тут будуть тільки сформульовані (без відповідних доведень) теореми, які нададуть нам можливість виконувати певні дії над парами сил. З доведенням даних теорем можна ознайомитись в додатку 4.
Теорема 1.
Дія пари сил на тверде тіло не зміниться, якщо пару сил в площині її дії перемістити в будь-яке положення (рис. 33).
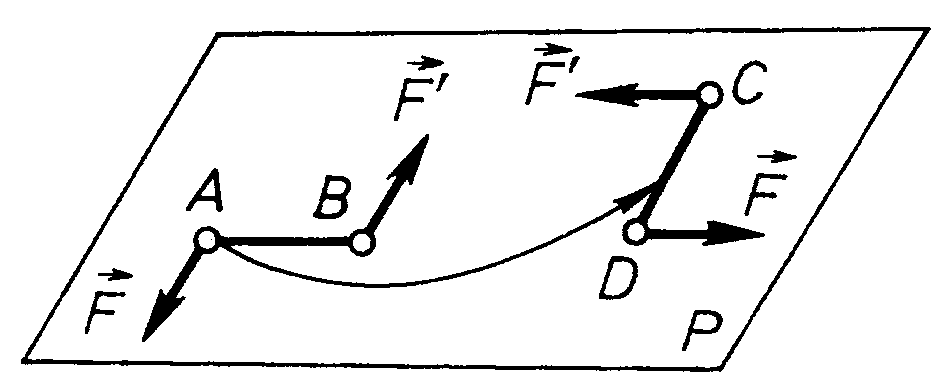
Рис. 33
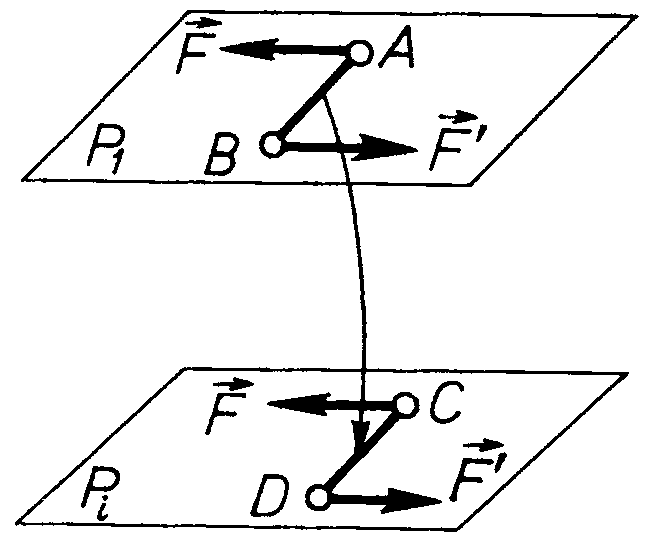
Теорема 2.
Дія пари сил на тверде тіло не зміниться, якщо пару сил перемістити в площину, яка паралельна площині дії пари сил (рис. 34).
Теорема 3.
Дія пари сил на тверде тіло не зміниться, якщо змі-нити сили пари і плече пари, залишивши без змін момент пари.
Для
пар сил, показаних на рис. 35,
![]() і
і
![]() .
З рівності
.
З рівності
![]() випливає, що для еквівалентних пар сили
обернено пропорційні їх плечам.
випливає, що для еквівалентних пар сили
обернено пропорційні їх плечам.
Сформульовані три теореми можна об’єднати в одну:
пари сил, моменти яких геометрично рівні, є еквівалентними
![]() .
(1.36)
.
(1.36)
Рівність
(1.36) є необхідною і достатньою умовою
еквівалентності двох пар сил з моментами
![]() і
і
![]() .
.
Рис. 34 |
Рис. 35 |
На основі сформульованих теорем бачимо, що над парою сил, як елементом статики, можна виконувати такі дії:
пару сил можна переносити в площині її дії, включаючи і її поворот на будь-який кут;
пару сил можна переносити в будь-яку площину, яка паралельна площині дії заданої пари сил;
можна змінювати силу пари і її плече, не змінюючи моменту пари.
Виходячи зі сказаного та математичної класифікації векторів (вільний, невільний, ковзний), вектор моменту пари сил належить до вільного вектора.