Реактивное поле, рассчитанное в модели Онзагера, равно

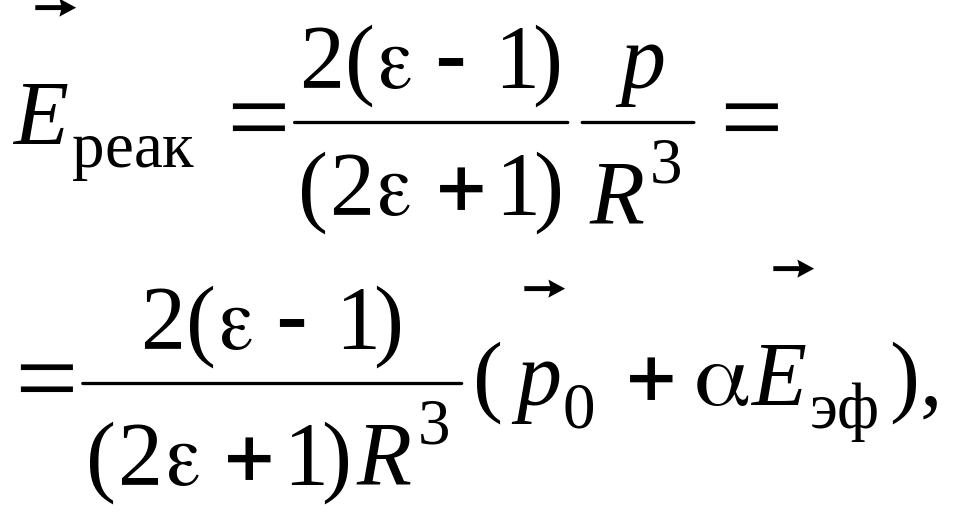(6.56)

где R – радиус полости, – результирующий дипольный момент молекулы. Реактивное поле, так как и поле внутри полости, можно выразить через показатель преломления среды:

. (6.57)

Таким образом, эффективное поле, действующее на молекулу в озагеровской полости равно

или

(6.58)

где и – функции от показателя преломления среды n (в общем случае n может быть комплексным), R – параметр теории, характеризующий объем полости.

Из формулы (6.58) видно, что свойства эффективного поля в области примесной молекулы существенно зависят от ее поляризуемости и параметра теории R. Если в единице объема находится N молекул, которые занимают объем , то R³ определяет эффективный объем, приходящийся на одну молекулу. Этот объем может быть рассчитан по известным значениям плотности и молекулярного веса для однокомпонентной среды.

Известно, что объем молекул очень тесно связан с ее поляризуемостью , входящей в формулу Лоренц – Лоренца. Анализ этой зависимости приводит к простому выражению .

Следовательно, онзагеровский радиус может быть оценен независимыми способами на основании различных характеристик вещества: показателей преломления или соответствующей величины рефракции, значения которых приведены в справочной литературе. Указанные способы применяются и к двухкомпонентным растворам, если радиусы молекулы и растворителя близки. Если радиус примесной молекулы больше, чем радиус молекулы растворителя, то онзагеровкий радиус для такой системы может быть выбран исходя из ван–дер–ваальсова радиуса исследуемой молекулы.

Модель Онзагера не лишена и некоторых недостатков:

1. модель шара с точечным диполем в центре не отражает реальных свойств молекулы, обладающей сложным расположением зарядов

2. нельзя рассматривать ближайшее окружение молекулы как сплошную среду с диэлектрической проницаемостью .

Недостаточно считать, что и связь данной молекулы с ее окружением выражается реактивным полем, имеющим то же направление, что и дипольный момент рассматриваемой молекулы. Логично предположить, что ориентация данной молекулы связана с ориентацией соседних молекул и, следовательно, зависит от их расположения.

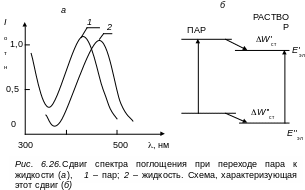
Несмотря на отмеченные недостатки с помощью этой модели можно рассчитывать взаимодействие растворенной молекулы с окружающей средой и определять положение ее электронно-колебательных уровней. Уровень энергии при переходе от газовой фазы к раствору смещается на величину так называемой энергии стабилизации W_ст, под которой будем понимать энергию уровня, которая установится после осуществления всех релаксационных процессов в молекуле после акта поглощения или испускания. Разность энергий стабилизации ΔW_ст = W'_ст + W''_ст основного и возбужденного уровней молекулы в растворе характеризует смещения спектра поглощения или испускания (см. рис. 6.26)

Величина сдвига спектра может быть записана в следующем виде:

,

где , и – изменения энергии молекулы в растворе, обусловленные взаимодействиями ориентационного, индукционного и дисперсионного характера. Энергия взаимодействия растворенной молекулы со средой определяется значениями ее дипольного момента , поляризуемости , а также величиной эффективного электрического поля , действующего на молекулу в растворе. Однако преимущества метода локального поля проявились еще и в том, что на его основе были рассчитаны динамические сдвиги полос в электронных спектрах поглощения. Влияние динамических индуктивно-резонансных взаимодействий на сдвиг частот максимумов полос спектров растворов был рассмотрен Бахшиевым в рамках описания общих закономерностей влияния растворителя на смещение электронных спектров при переходах от газовой фазы к раствору. Величина сдвига оценивается по формуле

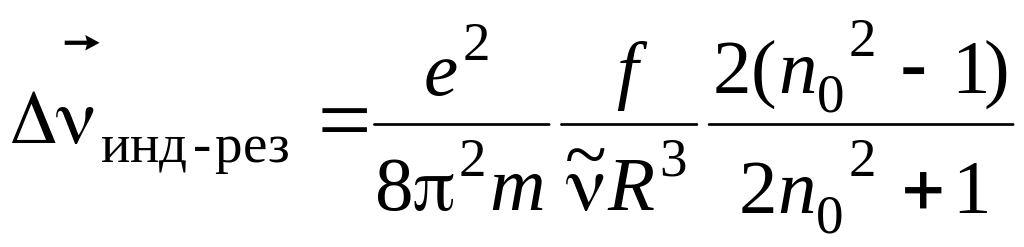, (6.59)

где e и m – заряд и масса электрона; f – сила осциллятора полосы; n₀ –показатель преломления растворителя; R – онзагеровский радиус молекулы; – частота максимума полосы

Принципиальное отличие динамических сдвигов от статических, рассматриваемых в теории Дебая, состоит в том, что динамические взаимодействия в конечном итоге определяются дипольным моментом перехода между квантовыми состояниями растворенной молекулы.

Итак, полный сдвиг частоты чисто электронного перехода для поглощения выразится в виде суммы

(6.60)

где – динамический сдвиг полосы, обусловленной возникновением у молекулы наведенного дипольного момента под действием электрического вектора световой волны.

В электронных спектрах поглощения смещение полос может достигать весьма значительной величины, равной тысячам см^–1. Причем полосы поглощения для одной и той же молекулы по разному сдвигаются в зависимости от растворителя. Например, спектр поглощения для молекулы 3-аминофталимида смещается в красную сторону в н-гептане на 1400 см^–1, а в этиловом спирте и воде – до 2300 см^–1.

В настоящее время установлены многие закономерности проявления межмолекулярных взаимодействий, имеющих самую разнообразную природу. Создан даже отдельный отдел спектроскопии межмолекулярных взаимодействий, который интенсивно развивается санкт-петербургской школой физиков (Бахшиев Н.Г., Либов В.С. и др.).

Источником информации в спектроскопии межмолекулярных взаимодействий о свойствах отдельных молекул служит не спектр молекулы как таковой, а изменение спектра при помещении молекулы в конденсированную среду.