
- •Глава 1. Общие вопросы спектроскопии молекул
- •1.1. Единицы измерения энергии и длины волны различных видов излучения
- •Переводные множители единиц измерения энергии
- •Длины волн, частоты и энергии различных диапазонов
- •1.2. Ширина уровней энергии и спектральных линий
- •1.3. Распределение молекул по уровням энергии
- •1.4. Вероятности оптических переходов
- •1.5. Квантовомеханический расчет вероятностей переходов
- •1.6. Правила отбора для различных типов излучения и поглощения
- •1.7 Поглощение света классическим электрическим осциллятором
- •Глава 2. Вращательные спектры молекул
- •2.1. Вращение двухатомной молекулы. Классический случай
- •2.2. Квантовомеханический случай
- •Значения вращательной энергии Евр двухатомной молекулы в зависимости от j
- •Вращательные постоянные , межъядерные расстояния re
- •2.3. Вращательные спектры многоатомных молекул
- •2.3.1. Деление молекул на сферические, симметричные и асимметричные волчки
- •2.3.2. Вращательные уровни энергии сферического волчка.
- •2.3.3. Вращательные уровни энергии и спектры молекул типа симметричного волчка
- •2.3.4. Уровни энергии и спектры молекул типа асимметричного волчка
- •Значения энергии вращательных уровней молекулы н2о, см–1
- •2.4. Применения вращательных спектров молекул
- •Вращательные постоянные (в см–1), межатомные расстояния и дипольные
- •Вращательные постоянные и структурные параметры некоторых
- •Глава 3.
- •3.1.Образование двухатомной молекулы. Представление о ее потенциальной кривой.
- •3.2. Колебания двухатомной молекулы как гармонического осциллятора
- •3.2.1. Механическая модель двухатомной молекулы
- •3.2.2. Квантовомеханический случай
- •3.3. Колебания двухатомной молекулы как ангармонического осциллятора
- •3.3.1. Аппроксимация зависимости потенциальной энергии от межьядерного расстояния в реальной молекуле (кривая Морзе)
- •3.3.2 Уровни энергии, правила отбора и спектры двухатомной молекулы как ангармонического осциллятора
- •3.4. Определение энергии диссоциации двухатомной молекулы
- •3.4.1. Аналитический метод
- •3.4.2. Метод графической экстраполяции (метод Берджа – Шпонер)
- •3.5. Колебательные спектры двухатомных молекул с изотопным замещением
- •3.6. Колебательно-вращательные спектры двухатомных молекул
- •3.6.1. Общая характеристика колебательно-вращательных
- •3.6.2 Колебательно-вращательные спектры. Ик-поглощения
- •3.6.3. Колебательно-вращательные спектры кр
- •3.6.4. Интенсивности линий вращательной структуры
- •Глава 4 колебательные спектры многоатомных молекул
- •4.1. Колебательные степени свободы многоатомной молекулы
- •4.2. Колебания многоатомной молекулы в классическом случае
- •4.3. Нормальные координаты и колебания.
- •4.4. Малые колебания в квантовой механике
- •4. 5. Классификация нормальных колебаний по форме
- •4.6. Симметрия молекул
- •4.6.1. Группа. Определение и основные свойства
- •4.6.2. Элементы и операции симметрии
- •4.6.3. Точечные группы симметрии и их элементы
- •Группы симметрии молекул
- •4.7. Примеры применения групповых законов к конкретным молекулам
- •Одно из возможных представлений группы с3
- •4.8. Представления группы симметрии. Линейные преобразования координат, соответствующие операциям симметрии
- •4.9. Выбор колебательных координат для характеристики колебательного движения атомов в молекулах
- •4.10. Анализ симметрии колебаний с помощью теории групп
- •4.11. Типы симметрии колебаний молекул
- •Типы симметрии колебаний и характеры представлений точечной группы симметрии d6h
- •4.12. Порядок нахождения числа колебаний различных типов симметрии
- •Характеры приводимых представлений молекулы воды точечной группы симметрии с.
- •Характеры приводимых представлений молекулы бензола точечной группы симметрии d6h
- •Интерпретация колебательного спектра бензола
- •Частоты и симметрия колебаний свободной и бидентатно-координированной нитратной группы
- •4.14. Спектры комбинационного рассеяния многоатомных молекул
- •4.15. Правила отбора в колебательных спектрах
- •Результирующая симметрия для сочетаний вырожденных состояний точечной группы симметрии d6h
- •4.16. Характеристические частоты колебаний молекулы
- •Характеристические частоты колебаний отдельных функциональных групп
- •Глава 5
- •5.1. Колебательная структура электронного спектра двухатомной молекулы
- •5.2.Относительная интенсивность полос в электронно-колебательном спектре двухатомной молекулы. Принцип Франка – Кондона
- •5.2.2. Квантовомеханический принцип Франка – Кондона
- •5.3. Химическая связь в двухатомной молекуле
- •5.3.1. Общие сведения о двухатомной молекуле
- •5.3.2. Основы метода молекулярных орбиталей (мо)
- •5.4. Типы химических связей в двухатомных молекулах. Σ- и π-связи
- •5.5. Систематика электронных состояний в двухатомной молекуле
- •5.6. Молекулярные электронные оболочки в двухатомной молекуле
- •5.7. Вращательная структура электронно-колебательных полос
- •5.8. Взаимодействие электронного и вращательного движений
- •5.9. Правила отбора в электронно-колебательно-вращательных спектрах двухатомных молекул
- •Глава 6 Электронные спектры многоатомных молекул
- •6.1. Электронные состояния и химические связи в многоатомных молекулах
- •6.1.1 Характеристика электронных состояний в многоатомных молекулах
- •6.2.2. Молекулярные орбитали молекулы формальдегида н2со
- •6.2.3. Молекула бензола с6н6
- •6.4. Некоторые вопросы теории электронно-колебательных спектров многоатомных молекул
- •6.4.1.Адиабатическое приближение
- •. Учет электронно-колебательного взаимодействия. Эффект Герцберга – Теллера
- •6.6. Электронные спектры поглощения ароматических соединений в газовой фазе
- •6.6.1 Бензол
- •6.7.1. Растворы. Ван-дер-ваальсово взаимодействие
- •Молекулярные постоянные и величины межмолекулярных взаимодействий в различных средах
- •6.7.2 Модель Онзагера
- •Реактивное поле, рассчитанное в модели Онзагера, равно
- •6.8. Электронные спектры поглощения растворов бензола и его производных
- •6.8.1. Общие замечания
- •6.8.2 Спектры растворов бензола и его производных с алкильными заместителями
- •6.8.3. Спектры поглощения производных бензола с заместителями, содержащими неподеленные пары электронов
- •6.9. Электронные спектры молекул в твердотельных матрицах. Эффект Шпольского
- •6.10. Электронные спектры поглощения молекулярных кристаллов
- •6.10.1.Общая характеристика молекулярного кристалла
- •6.10.2. Возникновение экситонных состояний в кристаллах. Давыдовское расщепление
- •6.10.3. Электронные спектры поглощения кристаллов бензола, нафталина и антрацена
- •Литература
5.8. Взаимодействие электронного и вращательного движений
Вращательная структура электронно-колебательных полос существенным образом зависит от свойств комбинирующих электронных состояний и особенно от силы спин-орбитальной связи. Известно, что для всех Σ-состояний проекция орбитального момента на ось молекулы равна нулю и взаимодействие спинового момента с орбитальным также равно нулю. Более высоко расположенные электронные состояния типа Π, Δ, ... начинают сравнительно сильно взаимодействовать со спиновым моментом молекулы.
Классификация различных типов связи электронных моментов молекулы с вращательными моментами была дана Гундом. По Гунду тип связи отличается различным порядком сложения электронных и вращательных моментов количества движения. Типов связи по Гунду различают несколько. Однако наиболее существенными являются два типа – случаи а и б по Гунду, которые различаются в зависимости от того, велико или мало мультиплетное расщепление, обусловленное спин-орбитальным взаимодействием, по сравнению с величиной вращательной энергии (вращательным моментом R).
Случай
а
имеет место, когда спин-орбитальное
взаимодействие достаточно велико, и
его нужно учитывать в первую очередь
по сравнению с величиной вращательной
энергии. Этот случай реализуется тогда,
когда электронный орбитальный момент
![]() и спиновый момент
и спиновый момент
![]() сильно связаны с осью молекулы, т. е.
имеют смысл только их проекции (обозначим
их соответственно
сильно связаны с осью молекулы, т. е.
имеют смысл только их проекции (обозначим
их соответственно
![]() и
и
![]() ).
Их проекции складываются в первую
очередь и дают полный электронный момент
Ω относительно оси.
).
Их проекции складываются в первую
очередь и дают полный электронный момент
Ω относительно оси.
![]() .
.
Причем
в отличие от
может быть как положительной величиной,
так и отрицательной. Значение Ω может
меняться от Λ + Z
до Λ – Z.
индексом
справа внизу указывают значения
![]() у Λ и одновременно индексом слева вверху
‑ мультиплетность æ = 2s
+ 1 с полной аналогией обозначения атомных
уровней при нормальной связи. Например,
при Λ и s 1
(æ = 3) число Z
может быть равно Z
= 1, 0, –1.
следовательно
Ω = Λ + Z = 2, 1, 0 и получаются
состояния 3Π2,
3Π1,
3Π0.
Спин-орбитальное взаимодействие приводит
к расщеплению Π-уровня на три подуровня
с различными значениями Ω.
у Λ и одновременно индексом слева вверху
‑ мультиплетность æ = 2s
+ 1 с полной аналогией обозначения атомных
уровней при нормальной связи. Например,
при Λ и s 1
(æ = 3) число Z
может быть равно Z
= 1, 0, –1.
следовательно
Ω = Λ + Z = 2, 1, 0 и получаются
состояния 3Π2,
3Π1,
3Π0.
Спин-орбитальное взаимодействие приводит
к расщеплению Π-уровня на три подуровня
с различными значениями Ω.
Для
каждого уровня с заданным значением Ω
нужно учесть сложение полного электронного
момента количества движения, направленного
вдоль оси молекулы, с вращательным
моментом количества движения
![]() ,
направленным перпендикулярно оси
молекулы. В результате этого суммирования
мы получаем полный момент количества
движения
,
направленным перпендикулярно оси
молекулы. В результате этого суммирования
мы получаем полный момент количества
движения
![]() как сумму
и
.
Квантовое число J
может принимать значение от Ω до Ω+1,
Ω+2, и т. д. до сравнительно больших
значений Ω пока еще возможно сохранение
молекулы. Согласно наглядным представлениям
картину сложения моментов поясняет
рис.5.19
как сумму
и
.
Квантовое число J
может принимать значение от Ω до Ω+1,
Ω+2, и т. д. до сравнительно больших
значений Ω пока еще возможно сохранение
молекулы. Согласно наглядным представлениям
картину сложения моментов поясняет
рис.5.19
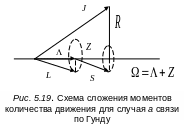
Электронный орбитальный момент и спиновый момент прецессируют вокруг оси молекулы, давая вектор , направленный по оси молекулы и равный . Этот вектор, складываясь с вектором вращательного движения , образует полный момент количества движения , вокруг которого прецессируют и . Вращательная энергия при этом выражается приближенной формулой:
![]() .
(5.82)
.
(5.82)
В результате для каждой составляющей мультиплетного терма, рассмотренного выше, получается своя последовательность вращательных уровней.
Случай связи а (по Гунду) имеет место при большом мультиплетном расщеплении, т. е. для вырожденных электронных состояний типа Π, Δ и др.
При
слабом взаимодействии спинового момента
с орбитальным моментом
реализуется случай связи б (по Гунду).
При этом сначала складывается вектор
проекции орбитального момента
с вектором вращательного момента
,
образуя полный момент количества
движения
![]() без учета
спина. Затем спиновый момент
складывается с вектором
,
и получается полный момент
с учетом
спина. Схема сложения моментов в случае
связи б
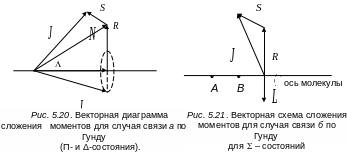
приведена на рис. 5.20. Для квантового
числа N
существует правило N
≥ Λ. Вращательная
энергия молекулы зависит главным образом
от значения квантового числа N,
спин только немного изменяет положение
уровней энергии.
без учета
спина. Затем спиновый момент
складывается с вектором
,
и получается полный момент
с учетом
спина. Схема сложения моментов в случае
связи б
приведена на рис. 5.20. Для квантового
числа N
существует правило N
≥ Λ. Вращательная
энергия молекулы зависит главным образом
от значения квантового числа N,
спин только немного изменяет положение
уровней энергии.
В синглетных состояниях (s = 0) векторы и совпадают. При s ≠ 0 для каждого значения N возможны 2s + 1 значений J:
J = N + S, N + S – 1, ...|N – S|
Поэтому вместо одного уровня с данным значением N существует 2s + 1 подуровней с различными возможными значениями J, немного различающимися по энергии. Таким образом, получается мультиплетное. расщепление вращательных уровней.
Векторная диаграмма сложения моментов для случая связи б по Гунду для состояний Σ-типа изображена на рис. 5.21).
В реальных молекулах случаи связи в вырожденных электронных состояниях являются, как правило, промежуточными между а и б по Гунду. Кроме того, при усилении вращения происходит постепенный «разрыв связи» спина с осью вращения (с ростом квантового числа J). Поэтому могут быть состояния, приближающиеся к случаю связи а (при малых значениях J) или к случаю б (при больших значениях J). Случаи а и б по Гунду являются предельными, возможны также промежуточные случаи.
Для дважды вырожденных уровней с Λ ≠ 0, наблюдается наряду с усложнением структуры, которое обусловлено наличием спина, явление Λ-удвоения. Оно состоит в расщеплении дважды вырожденных уровней под действием вращения. Различие в энергии расщепления будет тем больше, чем сильнее молекула вращается.
