5.5. Систематика электронных состояний в двухатомной молекуле

Для систематики электронных состояний в двухатомных молекулах, аналогично как и в атомах, вводятся определенные квантовые числа, характеризующие орбитальное и спиновое движение электронов. Наличие электрических и магнитных полей как в молекулах, так и в атомах, приводит к векторному сложению орбитальных и спиновых моментов количества движения. Однако в двухатомной молекуле валентные электроны движутся не в сферически-симметричном электрическом поле, что характерно для атома, а в аксиально-симметричном, что характерно для двухатомных или линейных многоатомных молекул. Все двухатомные молекулы относятся к двум типам симметрии: D_∞h или С_∞. К первому типу относятся молекулы, состоящие из одинаковых атомов, ко второму – из разноименных. Ось бесконечного порядка направлена вдоль химической связи. в том же направлении действует и электрическое поле, которое сильно влияет на полный орбитальный момент, вызывая его прецессию вокруг оси поля. В результате этого полный орбитальный момент перестает квантоваться, а сохраняется лишь квантование его проекции L_z на ось молекулы:

L_z = m_L· ħ, (5.65)

где m_L – квантовое число, принимающее значения m_L = 0, ±1, ±2 и т. д. При этом энергия электронного состояния зависит только от абсолютного значения m_{L ,} что соответствует тому факту, что с наглядной точки зрения оба вращения электрона (правое и левое) вокруг оси молекулы приводят к одному и тому же значению энергии. Введем некоторую величину Λ, которая характеризует абсолютную величину проекции полного орбитального момента на ось молекулы. Тогда значения Λ будут целыми положительными числами, различающимися на одну единицу Λ = m_L = 0, 1,2, ...

Для классификации электронных состояний двухатомной молекулы числа Λ играют ту же роль, что и орбитальное квантовое число l для классификации электронных состояний атомов. Общее суммарное квантовое число для атомов принято обозначать , где суммирование производится по всем электронам атома. Если L = 0, то такие электронные состояния обозначаются буквой s; если L = 1, то электронные состояния обозначаются буквой р., т. е.

	s, p, d, ...
L=	0, 1, 2, ...

Пользуюясь обозначениями электронных состояний для атома, электронные состояния для молекулы с последовательными значениями Λ принято обозначать прописными греческими буквами:

Λ=	0, 1, 2, 3, ...
состояния	Σ, Π, Δ, Φ, ...

Для двухатомных молекул обычно приходится иметь дело со значениями Λ, не превышающими 2. Для нормальных состояний молекул Λ преимущественно равно 0 (Σ-состояния). Возбужденные состояния двухатомных молекул имеют в большинстве случаев Λ = 0 и Λ = 1 (Σ- и П-состояния).

Все значения энергии с Λ ≠ 0 являются дважды вырожденными, что соответствует двум значениям проекции орбитального момента – положительным и отрицательным (m_L = Λ и m_L = –Λ). Σ-состояния, для которых Λ = 0, являются невырожденными.

На полный спиновый момент молекулы S, в отличие от полного орбитального момента L, аксиально-симметричное электрическое поле не действует. Поэтому полный спиновый момент S квантуется обычным образом приближенно сохраняя свое значение. При заданном значении S полный спиновый момент может ориентироваться æ = 2s + 1 способами, что для молекулы, аналогично как и для атома, определяет мультиплетность æ электронных состояний. В зависимости от значений æ состояния могут быть синглетными (æ = 1), дублетными (æ = 2), триплетными (æ = 3) и т. д. индекс, указывающий мультиплетность, ставится слева вверху соответствующей прописной буквы.

Например, синглетные состояния ¹Σ, ¹Π, ¹Δ, ...,

дублетные ‑ ²Σ, ²Π, ¹Δ, ...,

триплетные ‑ ³Σ, ³Π, ³Δ, ...

Для характеристики электронных состояний линейных молекул важную роль играют элементы симметрии σ_ для гетеронуклеарных (молекул с разными атомами) и центр инверсии i гомонуклеарных молекул (с одинаковыми атомами). По отношению к отражению в плоскости симметрии σ_, проходящей через ось молекулы, электронные состояния разделяются на положительные (+) и отрицательные (–). Для положительных состояний электронов волновая функция не меняет знак при отражении в плоскости σ_, а для отрицательных состояний ‑ меняет на противоположный, т. е.

Следовательно, все Σ-состояния как невырожденные, являются либо положительными (Σ⁺), либо отрицательными (Σ^–). Все дважды вырожденные состояния, для которых Λ ≠ 0, представляют собой совокупность положительных и отрицательных состояний. Если вырождение снимается, то дважды вырожденный уровень расщепляется на два, один из которых будет положительным, а другой ‑ отрицательным.

Если молекула относится к точечной группе D_∞h, то электронные состояния делятся по отношению к отражению в центре на четные (g) и нечетные (u). Каждое электронное состояние является либо четным, либо нечетным:

Σ_g⁺, Σ_g^–, Π_g, Δ_g, ...

Σ_u⁺, Σ_u^–, Π_u, Δ_u, ... .

Таким образом, имеется четыре типа Σ-состояний и по два типа П-, Δ-состояний.

Волновые функции оператора проекции орбитального момента количества движения имеют вид

.

При Λ = 0 это значение дает одну функцию . Если Λ≠0, то получаются две функции

Закон совместного преобразования функций и дает характеры для вырожденных состояний Π, Δ, Φ,...

Если волновые функции и не обладают в отдельности свойством положительности или отрицательности по отношению к операции σ_, то их линейные комбинации

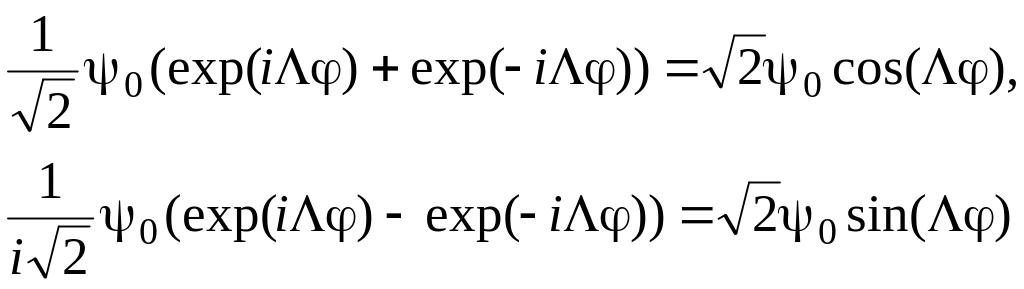
обладают этим свойством (это проверяется подстановкой φ = –φ).

Важно отметить, что из определенных электронных состояний исходных атомов возникает вполне определенный набор электронных состояний молекулы. На основании свойств симметрии можно установить характеристики этих состояний – значения квантовых чисел Λ и S, положительность или отрицательность Σ-состояний, четность или нечетность состояний для молекул, состоящих из одинаковых атомов. При каждом значении Λ состояния могут быть различной мультиплетности.

Спиновые моменты и атомов при образовании молекулы векторно складываются в полный спин молекулы . Возможные значения спинового квантового числа молекулы равны

S = S₁ + S₂, S₁ + S₂ –1, ... , |S₂ – S₁ |.

Соответственно мультиплетность æ состояния молекулы при заданных мультиплетностях æ₁ и æ₂ состояний атомов будет принимать значения

æ = æ₁ + æ₂–1, æ₁ + æ₂ – 3, ... , |æ₁ – æ₂| + 1.

Например, при æ₁ = æ₂ = 2 имеем æ = 3, 1; при æ₁ = 3, æ₂ = 2 имеем æ = 4, 2; при æ₁ = æ₂=3 имеем æ = 5, 3, 1.

Рассмотрим несколько примеров получения состояний молекулы, если известны состояния атомов, из которых образована молекула.

Пусть из двух s-состояний атомов образуется молекула. Например, два атома водорода в основном состоянии ²s образуют молекулу водорода. Орбитальные моменты электронов равны нулю, следовательно, образуются только Σ-состояния. В состоянии s находится только один электрон со спином s = 1/2, т. е. æ₁ = æ₂ = 2. поэтому образуются два состояния æ =3, 1. Таким образом образуется молекула в двух состояниях ¹Σ_g⁺ и ³Σ_g ^–.

Из двух атомов азота в основном состоянии ⁴s возникают состояния молекулы азота N₂ (æ = 1,3,5,7, æ₁ = 4 и æ₂ = 4) следующего вида ¹Σ_g⁺, ³Σ_u⁺, ⁵Σ_g^–, ⁷Σ_u⁺. Из двух атомов кислорода в основном состоянии ³p (æ=1,3,5) получаются следующие состояния молекулы:

а) синглетные ¹Σ_g⁺, ¹Σ_g⁺, ¹Σ_u^–, ¹Π_g ,¹Π_u, ¹Δ_g

б) триплетные ³Σ_u⁺, ³Σ_u⁺, ³Σ_g^–, ³Π_g ,³Π_u, ³Δ_u

в) квинтетные ⁵Σ_g⁺, ⁵Σ_g⁺, ⁵ Σ_u^–, ⁵Π_g ,⁵Π_u, ⁵Δ_g

Таким образом, Σ-состояний получается столько, сколько раз комбинация орбитальных моментов атомов равна нулю (0 + 0=0, 1 – 1 = 0, –1 + 1 = 0), Π-состояние получается столько, сколько раз орбитальное результирующее квантовое число равно 1 или –1 (Π-состояния дважды вырождены) (1 + 0 = 1 и –1 + 0 = –1, 0 + 1 = 1 и 0 – 1 = –1). Δ-состояний получается столько, сколько раз результирующий орбитальный момент равен 2 или –2.

Как видно, число получающихся состояний может быть большим. Однако устойчивыми оказываются только те состояния, которым соответствует минимум потенциальной энергии, остальные – неустойчивыми. Определить устойчивость или неустойчивость электронных состояний можно только на основе квантовомеханических расчетов энергии химических связей. Например, расчет на основе квантовой механики энергии связи для молекулы H₂ позволил установить, что из двух возможных состояний ¹Σ_g⁺ и ³Σ_u⁺, возникающих при взаимодействии атомов водорода в основном состоянии ²s, первое устойчиво и является основным состоянием молекулы, а второе неустойчиво (ему соответствует типичная кривая отталкивания). В таблице 5.1 приведены обозначения термов основного состояния некоторых двухатомных молекул, межатомные расстояния и энергии химической связи.

Таблица 5.1

Электронные состояния, межатомные расстояния и энергия химической связи некоторых двухатомных молекул.

Молекула	Электронная конфигурация основного состояния	Межатомное расстояние, Ǻ	Энергия связи, эВ
H2 H2+ He2 He2+	(σg)2, 1Σg+ (σg)1, 2 Σg+ (σg)2 (σu*)2, 1Σg+ (σg)2 (σu*)1, 2Σu+	0,07415 0,106 – 1,108	4,48 2,65 ~0 ~3
O2	(πu)4 (σg)2 (πg*), 3Σg–	0,120741	5,1
O2+	(πu)4 (σg)2 (πg*), 2Пg	0,11227	6,48
O2–	(πu)4 (σg)2 (πg*), 2П (?)	0,126	–
N2	(πu)4 (σg)2, 1Σg+	0,10976	9,75
N2+	(πu)4 (σg)1, 2Σg+	0,1116	8,73
C2	(πu)3 (σg)1, 3Пu	0,1117	6,5
F2	(πu)4 (σg)2 (πg*)1, 1Σg+	0,1418	1,56
LiH	(σs)2, 1Σ+	0,15953	2,51
BeH	(σs)2 (σs*)1, 2Σ+	0,13431	2,29
CH	(σs)2 (σs*)2 (π)1, 2П	0,11198	3,47
CO	(σs) 2 (πx,y)4, 1Σ	0,11282	11,08
CN	(πx,y)4 (σs) 1, 2Σ+	0,11718	8,15
CF	(σs)2 (π*)1, 2П	0,127	6,59
NO	(πx,y)4 (σs)2 (π*)1, 2Π	0,1150	8,02
NP	(πx,y)4 (σs)2, 1Σ	0,14910	5,98
PO	(πx,y)4 (σs)1, 2Π	0,1448	5,42
NH	(σs)2 (σs*)2 (πx,y)2 , 3Σ–	0,1038	3,69
HF	(σs)2 (σs*)2 (πx,y)4, Σ	0,09175	5,81