5.2.Относительная интенсивность полос в электронно-колебательном спектре двухатомной молекулы. Принцип Франка – Кондона

В предыдущем параграфе мы рассмотрели всевозможные прогрессии полос в электронно-колебательном спектре двухатомной молекулы, ничего не говоря об интенсивности этих полос, которая успешно рассчитывается методами квантовой механики. Для качественного рассмотрения картины распределения интенсивности полос в сериях пользуются системой потенциальных кривых нижнего и верхнего электронных состояний, построенных по принципу Франка – Кондона. Этот принцип основывается на адиабатическом приближении, утверждающем, что в молекуле «быстрая» подсистема (электроны) движется гораздо быстрее, чем «медленная» (ядра), в силу различия их масс. При одном колебании ядер, происходящем за время порядка 10^–12с, электронная подсистема может совершить тысячи оборотов вокруг ядра.

Согласно принципу Франка – Кондона, электронный переход в молекуле происходит настолько быстро (за время τ ≈ 10^–15 с в видимой области спектра), что за это время колеблющаяся молекула не может заметно изменить ни своего положения (межъядерного расстояния), ни своей энергии (импульсов ядер). Иными словами, медленная ядерная подсистема не успевает среагировать за «быстрой» (электронной). В этом заключается смысл принципа Франка – Кондона в его классической формулировке.

Е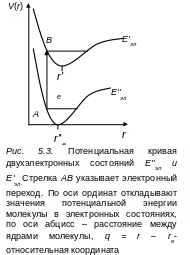 сли электронноколебательный переход на диаграмме потенциальных кривых изображен стрелкой, начало которой показывает энергию и координату колебания в момент начала перехода, а конец фиксирует энергию и координату в момент времени, следующий за электронным переходом, то условие q = r – r_e = const означает, что стрелка должна быть вертикальной. Второе условие p = const или T = const означает, что если стрелка начинается на потенциальной кривой (точка А на рис. 5.3), то и оканчивается она на потенциальной кривой (точка В) возбужденного электронного состояния. Точки А и В на рис. 5.3 являются поворотными точками колебательного движения комбинирующих электронных состояний. скорость в этих точках равна нулю. Квантовомеханическое рассмотрение приводит к выводу, что возможны и переходы, соответствующие изменениям расстояния между ядрами и их скоростей. однако вероятность таких переходов тем меньше, чем больше эти изменения.

В классическом подходе предполагается, что осциллятор в момент электронного перехода находится только в поворотных точках классического движения. В этих точках кинетическая энергия его равна нулю. На диаграмме потенциальных кривых, изображающие переход стрелки начинаются и оканчиваются на потенциальных кривых (рис. 5.3).

Рассмотрим распределение интенсивности полос колебательной структуры по принципу Франка – Кондона.

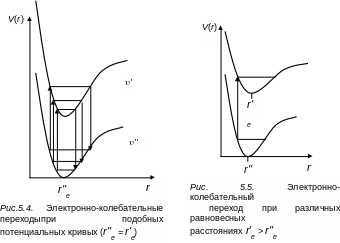
1. Пусть потенциальные кривые комбинирующих состояний подобны друг другу и соответствуют одинаковому равновесному расстоянию r''_e = r'_e (рис. 5.4). Наиболее вероятны переходы между колебательными подуровнями с одинаковыми '' и '. Поворотные точки классического движения расположены друг над другом. По мере увеличения разности Δ = ' – '' вероятность переходов будет убывать. На рис.5.4 наиболее интенсивными будут переходы при Δ = 0, слабее будут группы полос Δ = +1(в поглощении) и Δ = –1 (в испускании), еще слабее группа полос Δ = +2, Δ = –2.

Рассмотренный случай не является типичным для двухатомных молекул, так как при возбуждении молекулы изменяется ее равновесное расстояние (как правило r''_e < r'_e). Если рассмотреть расположение кривых потенциальной энергии, которое приведено на рис. 5.5, то при переходах с нулевого колебательного уровня '' = 0 нижнего электронного состояния наиболее вероятен переход на колебательный подуровень возбужденного электронного состояния ', отличный от ''. Переходы на подуровень ' больше заданного менее вероятны (будем наблюдать поперечную серию Деландера). Максимум поглощения получится при некотором фиксированном '. в обе стороны от этого максимума интенсивность спадает.

При испускании с колебательных подуровней ' верхнего электронного состояния или при поглощении с высоких колебательных подуровней '' нижнего электронного состояния наиболее вероятными будут переходы, обозначенные на рис. 5.6 стрелками. С двух верхних колебательных подуровней на два нижних колебательных подуровня (в испускании случай а) или наоборот (в поглощении случай б).

Если представить распределение вероятности переходов в схеме типа Деландера, то наиболее вероятные переходы будут получаться для полос, лежащих (согласно схеме Деландера) на параболе, которую называют параболой Кондона (рис. 5.7). При заданном значении ' получаются два значения '', а при заданном '' – два значения ', соответствующих максимальной вероятности перехода. На рис. 5.7 штриховой отрезок прямой линии пересекает параболу в двух точках.

При одинаковом равновесном расстоянии (r''_e = r'_e) парабола Кондона превращается в диагональную прямую (т. е. максимальные вероятности перехода получаются при ' = ''). Распределение интенсивности в поглощении в соответствии с параболой Кондона может наблюдаться при возбуждении большого числа колебательных уровней нижнего состояния. Это соответствует достаточно высокой температуре.

А налогичное распределение интенсивностей в испускании можно наблюдать, если возбуждено достаточно большое число колебательных уровней верхнего электронного состояния.

5.2.1. Полуклассический вариант принципа Франка – Кондона

При формулировке принципа Франка-Кондона в классическом варианте мы исходим из того, что при электронном переходе q = r – r_e = const и Т = const Однако с точки зрения квантовой механики нельзя одновременно фиксировать координаты и импульс частиц. Тем не менее в адиабатическом приближении мы полагали, что квантовые эффекты для столь массивных частиц, как ядра, выражены очень слабо. Далее мало обоснованным было положение, что стрелки, указывающие переход, должны начинаться с потенциальной кривой одного состояния (где скорости ядер равны нулю) и оканчиваться на потенциальной кривой другого электронного состояния. Последнее положение нельзя обосновать в полуклассическом рассмотрении. Его следует заменить новым положением следующего содержания. Электронные переходы могут иметь место при любых значениях колебательной координаты q (а не только при q_max) с вероятностями W(q), где W(q) есть квантовомеханическое распределение координаты. Если интересоваться переходами из одного определенного исходного колебательного состояния, то вероятность распределения координаты является квадратом модуля волновой функции в координатном представлении, т. е.

W (q) = |Ψ_(q)|². (5.11)

На диаграмме потенциальных кривых полуклассический принцип разрешает переходы из любых точек уровня энергии колебательного перехода, а не только поворотных точек классического движения, где осциллятор пребывает большую часть времени. Если '' = 0, то наибольший вес приобретает стрелка, запрещенная по классическому варианту принципа Франка–Кондона, так как в области малых квантовых чисел, особенно при '' = 0 и ' = 0, классическое распределение координаты коренным образом отличается от квантовомеханического распределения (см. гл. 3).

Может оказаться, что требование q = const и Т = const приводит к существенным погрешностям в интенсивностях полос, когда речь идет о переходах, начинающихся с нулевого колебательного уровня. Оказывается, что это не так, особенно если учесть, что и амплитуда колебаний ядер при  = 0 достаточно мала. Специальное рассмотрение показывает, что точность полуклассического принципа Франка – Кондона зависит в основном от номера  конечного колебательного уровня, достигаемого в процессе перехода. Если важная для электронно-колебательного перехода область лежит при больших  ( ≥ 10), то полуклассический принцип Франка – Кондона дает результаты, достаточно близкие к квантовомеханическим.

Рассмотрим распределение интенсивности по полосам в электронно-колебательном спектре на основании полуклассического варианта принципа Франка-Кондона. Обратимся к рис 5.8, который наглядно иллюстрирует различные сдвиги потенциальных кривых нижнего и верхнего электронного состояний. Первый случай (см. рис.5.8, а) соответствует r''_e = r'_e Квантовые колебательные уровни обозначены горизонтальными линиями, на которых изображены квадраты модулей волновых функций, характеризующих вероятность распределения координат ядер.

Этот случай соответствует равенству минимумов потенциальной энергии двух электронных состояний и подобию кривых потенциальной энергии. Из рис.5.8, а видно, что произведение Ψ_''·Ψ_' достигает наибольшего значения при '' = ' = 0. Интеграл перекрывания двух волновых функций будет большим, что приведет к наиболее вероятным переходам. Наибольшую интенсивность будет иметь 0–0 полоса. Примером может служить спектр поглощения молекулы кислорода в видимой области (760 нм), обусловленный переходом . Этот переход, вообще говоря, запрещен, но он иногда возникает благодаря нарушению правил отбора при столкновении молекул.

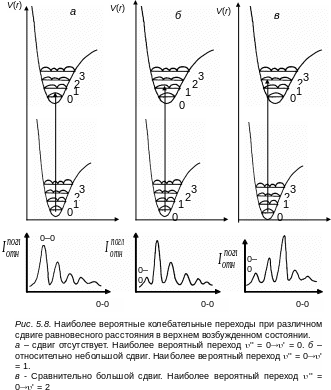
Рассмотрим переходы в случае, когда равновесное расстояние в возбужденном состоянии мало увеличено по сравнению с равновесным расстоянием основного состояния (см. рис.5.8, б). В согласии с принципом Франка-Кондона здесь наибольшей интенсивностью будет обладать переход 0→1. при еще большем смещении потенциальных кривых, наиболее интенсивным может быть переход 0→2 и т.д.

Дальнейшее увеличение r''_e приводит к появлению спектра поглощения, в котором полосы, сближаясь, переходят в непрерывную зону (континиум). Этот случай изображен на рис. 5.8, в. Примером подобного рода спектров может быть спектр поглощения паров йода в видимой области или систем полос Шумана – Рунге молекулы кислорода в ультрафиолете (короче 200 нм), переход .