4.11. Типы симметрии колебаний молекул

Формы нормальных колебаний молекулы при выполнении операций симметрии преобразуются определенным образом. Нормальные колебания характеризуются типами симметрии, которые определяются совокупностью всех преобразований формы колебания.

Если при операции симметрии форма нормального колебания не изменяется, т. е. координаты симметрии не изменяются, то такие колебания называются симметричными.

Если при операции симметрии форма колебания изменяется так, что координаты симметрии умножаются на – 1, то такое колебание называется асимметричным. Если при операции симметрии координаты симметрии умножаются на число, не равное ±1, то такое колебание называется вырожденным.

Существуют следующие типы симметрии колебаний:

1. Колебания, симметричные по отношению ко всем операциям симметрии или элементам, определяющим эти операции, называются полносимметричными;

2. Колебания, асимметричные по отношению к некоторым элементам симметрии – неполносимметричные.

3. Колебания, вырожденные хотя бы к одному элементу симметрии – вырожденные.

Приняты следующие обозначения типов симметрии:

А – колебания, симметричные относительно поворотной оси симметрии;

В – колебания, антисимметричные относительно этой оси. Индекс 1 (например, А₁, В₁) означает симметрию колебания относительно плоскости _, проходящей через поворотную ось, индекс 2 – антисимметрию относительно этой плоскости. Индексы один штрих и два штриха справа вверху означают соответственно симметрию или антисимметрию относительно горизонтальной плоскости _h, перпендикулярной поворотной оси (например, А^'₁ и А^"₂ , В^'₁ и В^"₂). Индексы g и u, которые ставятся справа внизу после цифры означают симметрию или антисимметрию колебания относительно центра симметрии (инверсии). Например, колебание типа A_1g, является полносимметричным, оно симметрично относительно всех элементов симметрии. Колебания дважды вырожденных типов симметрии обозначаются буквой Е с соответствующими индексами. Колебания трижды вырожденного типа – F. Число типов симметрии зависит от группы симметрии и равно числу классов элементов данной группы.

Рассмотрим преобразования координат симметрии при операциях симметрии на примере трехатомной молекулы воды Н₂О, точечная группа симметрии C_2 (см. рис. 4.14 и 4.15). В табл. 4.5 приведены коэффициенты, на которые умножаются координаты симметрии при операциях симметрии.

Действительно, при повороте на угол 180° симметричная координата должна умножаться на –1, чтобы перейти в антисимметричную. То же происходит и при отражении в плоскости _^^.

Таблица 4.5

_{Таблица коэффициентов точечной группы C2}

Операции симметрии
Координаты симметрии	C1  I	C2	 ()	 ()
qs	1	1	1	1
qas	1	–1	1	–1
qs	1	1	1	1

Из таблицы 4.5 видно, что для молекулы воды возможны два полносимметричных колебания (q_s, и q_s^) – координаты симметрии не изменяются при всех операциях симметрии – и одно неполносимметричное колебание (координаты q_as при операциях C₂ и  умножаются на –1).

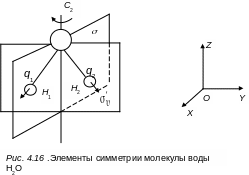
Рассмотрим представление группы C_2 в естественных координатах на примере трехатомной молекулы Н₂О (q₁, q₂, q₃^) (см. рис. 4.16)

При повороте вокруг оси С₂ координаты преобразуются так:

,

, (4.77)

.

При повороте вокруг оси C₁ (операция идентичности) и отражения в плоскости _^^координаты преобразуются таким образом

,

, (4.78)

.

При операции отражения в плоскости _^^ получаем:

,

, (4.79)

.

результаты можно представить в табл. 4.6. Можно проверить, что совокупность матриц в этой таблице образует группу. В координатах симметрии (q_s, q_as, q_s^) получается другое представление группы С_2. Закон преобразования координат симметрии в этом случае будет следующим:

при операции С₂ имеем:

,

, (4.80)

;

при операции С₁ и отражении в плоскости _^^ получим:

,

, (4.81)

;

при операции отражения в плоскости _^^:

,

, (4.82)

.

Полученные преобразования можно представить следующей таблицей:

Таблица 4.7

Матрицы преобразования координат симметрии для молекулы Н₂О

	Операции симметрии
Матрицы преобразования	С1I	С2	()	()

Представление группы С_2 в координатах симметрии обладает той особенностью, что матрицы всех преобразований являются диагональными, т. е. каждая матрица 3-го ранга распадается на три матрицы 1-го ранга. Совокупность матриц первого ранга образует неприводимое представление группы С_2, так как дальнейшее понижение ранга этих матриц уже невозможно.

Представление группы симметрии С_2 в естественных координатах является приводимым, так как преобразованием координат его можно разложить на неприводимые представления. Таким образом, мы получим два одинаковых одномерных неприводимых представления Г₁ (тип А₁), отвечающие полносимметричному валентному колебанию О–Н и деформационному симметричному колебанию (изменение угла ). Кроме того, получилось одно неприводимое представление Г₂ (тип В₂), соответствующее неполносимметричному валентному колебанию.

Итак, полное представление группы симметрии С_2 распадается на два представления типа Г₁ и одно представление типа Г₂. С точки зрения колебаний молекулы Н₂О три ее колебания распадаются на два колебания типа А₁ и одно колебание типа В₂, т. е.

.

Итак, в молекуле Н₂О имеются два колебания полносимметричного типа ( и ) и одно колебание ( ) – антисимметричного типа.

Оказывается, что определение типов симметрии нормальных колебаний возможно и в общем виде для молекул, принадлежащих к любой точечной группе. Для этого необходимо учитывать только характеры матриц, описывающих те или иные операции в группах симметрии.

Для молекул, принадлежащих к группам низшей симметрии, число типов симметрии равно числу элементов группы, т. е. ее порядку. Следовательно, оно равно 2 для групп второго порядка (С_i, C_s и C₂) и 4 для групп четвертого порядка (С_2 и С_2h). Для точечной группы более высокой симметрии число типов колебаний меньше порядка группы. В качестве примера приведем таблицу характеров и обозначений типов симметрии молекулы бензола, точечной группы D_6h (табл. 4.8).

Таблица 4.8