1.3. Распределение молекул по уровням энергии

Интенсивность линий или полос в спектрах поглощения и испускания зависит не только от вероятности переходов между уровнями энергии, но и от заселенности уровней, т.е. от того, сколько молекул находится на исходном уровне Е_i при заданной температуре Т. Существует закон, установленный Больцманом, показывающий, как распределены молекулы по энергетическим уровням в условиях теплового равновесия. Число молекул на i-м уровне описывается экспоненциальной функцией вида

n_i = Сnexp(–E_i / kT), (1.29)

где n – общее число молекул, С – постоянная, зависящая от температуры, Е_i – энергия уровня, k – постоянная Больцмана, Т – абсолютная температура.

Из соотношения (1.29) видно, что при стремлении температуры к абсолютному нулю (Т → 0) число молекул на i-м уровне также стремится к нулю, т. е. при температуре абсолютного нуля все молекулы будут находиться на нулевом уровне энергии.

Введем некоторые определения. Пусть в единице объема находится n молекул, обладающих определенным запасом энергии. В соответствии с законом (1.29) различные молекулы могут находиться в различных энергетических состояниях. Каждому энергетическому уровню Е_i-му, если система обладает дискретным набором значений энергии Е₁, Е₂, …,Е_i, будет соответствовать число молекул, равное n_i. Полное число молекул n будет таким образом равно

. (1.30)

Разделив правую и левую части равенства (1.30) на n, получим

, (1.31)

где ρ_i есть n/n_i и характеризует долю частиц на i-м уровне энергии. Совокупность значений ρ_i, характеризующих долю молекул в том или ином энергетическом состоянии, назвали функцией распределения. Как видно из соотношения (1.31), функция распределения нормирована.

Функцию распределения молекул по энергетическим уровням можно ввести и для сплошного спектра значений энергии, когда рассматривают молекулы конденсированной среды. Для этого введем число молекул dn(E), обладающих энергиями в интервале значений от Е до Е + dE. Пусть ρ(Е) – функция распределения молекул в сплошном спектре. Тогда

ρ(Е)dE = dn(E)/n, (1.32)

где ρ(Е) характеризует долю молекул, находящихся в единичном интервале значений энергии. При нормировании этой функции операцию суммирования надо заменить интегрированием, т. е.

. (1.33)

Знание функции распределения для спектроскопии молекул имеет чрезвычайно важное значение, т к. она определяет не только интенсивность поглощения и испускания, но и другие особенности спектров. Вид функции распределения зависит от внутренних свойств молекул и характера внешних воздействий на систему, т. е. от условий проведения эксперимента. При введении понятия функции распределения не была принята во внимание степень вырождения уровней энергии Е_i (статистический вес уровня g_i). С учетом этого число молекул на вырожденных уровнях будет пропорционально статистическому весу уровня g_i.

Все типы распределения по уровням энергии можно разделить на равновесные и неравновесные. Равновесное распределение молекул зависит от особенностей окружающей среды и почти не зависит от конкретных свойств молекул. Оно носит универсальный характер и имеет существенное значение при процессах теплового поглощения или испускания. Равновесное распределение осуществляется при полном термодинамическом равновесии внутри системы и с окружающей средой. При этом выполняется принцип детального равновесия: какое количество энергии система получает от внешнего источника по определенным каналам, такое же количество она должна и отдавать по тем же каналам.

Неравновесное распределение возникает при нарушении термодинамического равновесия под действием внешних причин (воздействием на систему световых потоков, потоков электронов или других элементарных частиц). Вид неравновесных функций распределения будет зависеть как от характера, так и от интенсивности внешних воздействий, а также от того, как реагирует сама система на эти воздействия.

Неравновесные функции распределения подразделяются в свою очередь на стационарные и нестационарные. Первые распределения не зависят от времени и характеризуют энергетические состояния молекул спустя некоторое время после постоянного внешнего воздействия. В системе молекул в этом случае устанавливается динамическое (подвижное) равновесие: сколько энергии система получает по возможным каналам, столько же она и отдает окружению по другим каналам.

Согласно законам статистической физики при термодинамическом равновесии вид функции распределения задается следующим соотношением

, (1.34)

где g_i – статистический вес уровня (число независимых состояний системы, характеризующихся одним и тем же значением энергии Е_i), с(Т) – коэффициент, который находится из условия нормировки. Просуммировав справа и слева равенство по уровням энергии, получим:

, (1.35)

получим:

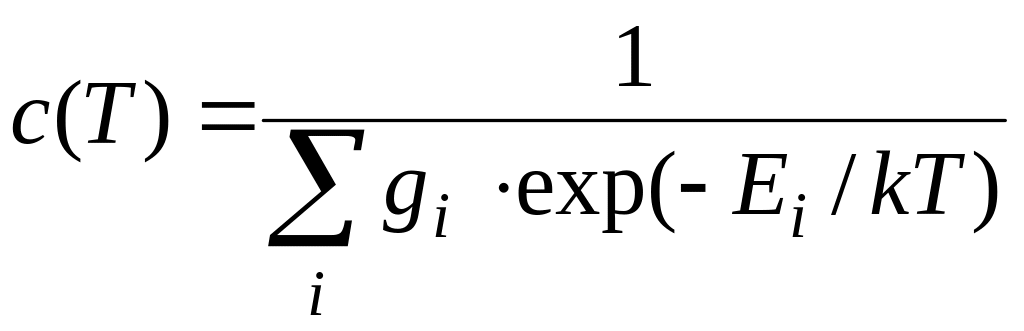, (1.36)

В случае сплошного энергетического спектра равновесная функция распределения имеет следующий вид

, (1.37)

где

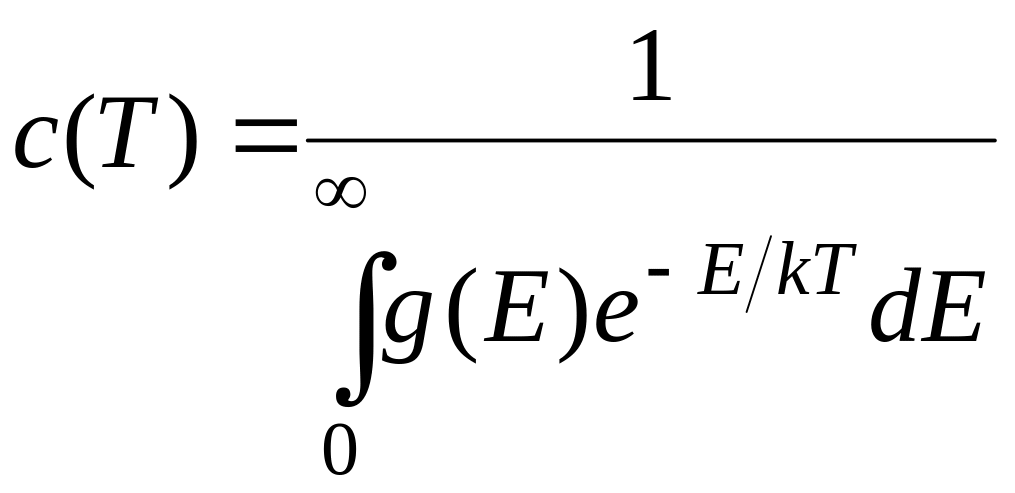(1.38)

В формуле (1.37) g(Е) характеризует статистический вес уровня сплошного спектра (число независимых состояний в единичном интервале значений энергии). Дело в том в том, что для молекулярной системы число уровней энергии, приходящихся на единичный интервал энергии (с учетом основных, кратных и составных уровней) возрастает с ростом энергии Е практически по линейному закону.

Знание коэффициентов с(Т) в формулах (1.34) и (1.37) необходимо только при изучении абсолютных значений интенсивности. При оценке относительных интенсивностей линий точного их значения не требуется.

С помощью выражения (1.34) найдем число молекул, находящихся в двух возбужденных состояниях i и k, причем состояние k более высокое. Возьмем отношение

. (1.39)

Пусть статистические веса уровней молекулы будут g_k = g_i = 1. тогда n_k/n_i = exp(–(E_k – E_i)/kT). Если E_k > E_i, то n_k/n_i меньше единицы, т. е. чем выше энергия состояния Е_k, тем меньше в нем молекул. Такое распределение молекул имеет место при термодинамическом равновесии. В неравновесной системе это распределение может быть нарушено, что типично для лазерных систем. Чтобы лазерная система генерировала излучение, необходимо создавать инверсную населенность уровней энергии, т. е. на k-м уровне число молекул должно быть больше, чем на i-м.

Произведем некоторые оценки населенностей уровней энергии, соответствующих колебательным степеням свободы молекулы E_k – E_i = = 1000 см^–1, Т = 293 К, kТ = 196 см^–1. Согласно уравнению (1.39) получим n_k/n_i = g_k/g_i·exp(–5). Принимая, что g_k = g_i = 1, а число молекул на нижнем уровне n_i примерно равно числу Лошмидта n_i ≈ 2,9∙10¹⁸ , то получим n_k ≈ 2,9∙10¹⁸∙674∙10^–5 ≈ 10¹⁶, т. е. на k-м уровне на два порядка молекул меньше, чем на основном.

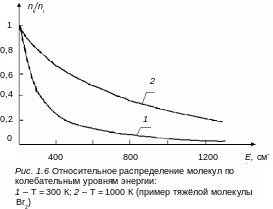
Если расстояние между колебательными подуровнями тяжелых молекул равно 200 см^–1, то n_k/n_i ≈ 0,37 , т. е. k-й уровень при комнатной температуре хорошо заселен. На рис. 1.6 приведены зависимости относительных распределений молекул по колебательным подуровням для двух температур молекулы Br₂, а на рис 1.7 приведены функции распределения молекул по колебательным подуровням в одном электронно-колебательном состоянии многоатомной молекулы (плотность колебательных состояний g(Е) возрастает линейно с увеличением Е).

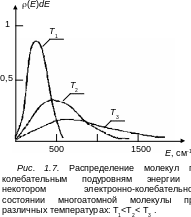
Как видим на рис.1.7, максимум функции распределения с уменьшением температуры Т приближается к нулевой колебательной энергии и в пределе при Т= 0 К все молекулы будут находиться на нулевом колебательном подуровне.