4.6.2. Элементы и операции симметрии

Рассмотрим более подробно отдельные элементы симметрии и соответствующие им операции симметрии.

1. Ось симметрии обозначают С_n, где n означает порядок оси и может принимать значения n = 1, 2, 3, 4, ... Элементу С_n соответствует операция поворота молекулы на угол 2/n, т. е. такая операция, при выполнении которой молекула переходит сама в себя (новая конфигурация молекулы не отличается от исходной, существовавшей до выполнения поворота). рассмотрим, например, молекулу бензола (рис. 4.7), обладающую наряду с другими элементами осью симметрии 6-го порядка С₆.

При всех операциях поворота на угол 2/n молекула переходит сама в себя. Отметим, что этот поворот можно совершать большое число раз в прямом и обратном направлениях (т. е. по часовой и против часовой стрелки), не нарушая равновесной конфигурации. Например, совершив операцию поворота С₆ три раза (это можно записать как ), мы повернем молекулу на 180° без нарушения равновесной конфигурации.

Совершив указанную операцию пять раз ( ), мы повернем молекулу на угол 300°. Указанного положения можно достигнуть повернув молекулу на угол – 60°. Записывается это следующим символом . Из сказанного ясно, что  . В общем виде оси С_n будет соответствовать n операций симметрии – поворотов вокруг оси на угол 2/n. В предельном случае при n возможны вращения на бесконечно малые углы или произвольные углы (непрерывные вращения).

Ось симметрии C₁ означает тождественный элемент симметрии. соответствующая операция симметрии оставляет молекулу неизменной, так как поворот на 360° равносилен его отсутствию (т. е. повороту на 0°).

На рис. 4.8. показано действие операции симметрии С₃ на ион NO₃^–. При этой операции атом кислорода О₁ переходит на место О₂, О₂ – на место О₃, а О₃ занимает место О₁. При этом последующая конфигурация не отличается от предыдущей (кислороды О₁, О₂ и О₃ тождественны).

Операцию симметрии С₃ можно повторять несколько раз . при этом симметрия равновесной конфигурации не изменяется.

Плоскость, в которой расположен ион NO₃^–, является плоскостью симметрии _h, а это уже следующий элемент симметрии.

2. Плоскость симметрии обозначают символом  с индексом  или h. Этому элементу симметрии соответствует операция отражения в плоскости, которая переводит молекулу в новую равновесную конфигурацию, неотличимую от первоначальной. Легко показать, что ² = I (рис. 4.8). _ – обозначает отражение в вертикальной плоскости, _h – то же в горизонтальной плоскости. Если в молекуле имеется несколько осей симметрии, то вертикальная или горизонтальная плоскости рассматриваются относительно оси высшей симметрии. В некоторых молекулах (например, бензол С₆H₆) присутствует элемент _d (диэдрическая плоскость симметрии).

3. Зеркально-поворотная ось порядка n обозначается символом S_n. Ей соответствует операция поворота на угол 2/n вокруг оси с одновременным отражением в плоскости _h ,. перпендикулярной к оси, т. е.

S_n = _hC_n = C_n _h (4.36)

Операции поворота C_n. и отражения _h коммутируют между собой. Зеркально-поворотная ось симметрии порядка n(S_n) является независимым элементом только для четного n. Действительно, для четного n имеется n операций:

П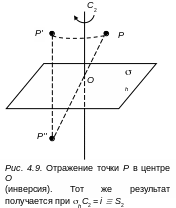 ри этом ось S_n одновременно является осью C_n/2, порядка n/2. При нечетном n зеркально-повторная оcь представляет собой сочетание оси симметрии С_n с плоскостью симметрии _h и не является независимым элементом симметрии.

4. Центр симметрии обозначается символом i. Ему соответствует операция симметрии i-отражение в центре (инверсия). Эту операцию с точки зрения групповых законов можно рассматривать как произведение операций поворота вокруг оси 2-го порядка с последующим отражением в плоскости, перпендикулярной к оси, т. е. i = _hC₂  S₂

На рис.4.9. показано действие операции инверсии на точку P в результате мы получаем точку P''. Этот же результат можно получить и путем поворота точки P на 180° с последующим отражением в плоскости б_h , перпендикулярной к оси вращения С₂.