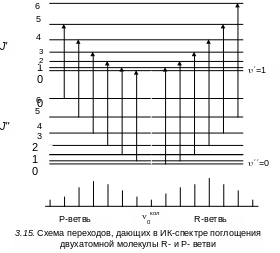
3.6.2 Колебательно-вращательные спектры. Ик-поглощения
Колебательно-вращательные спектры, соответствующие дипольным переходам в ИК области, подвержены следующим правилам отбора для вращательного квантового числа
J = J' – J" = 1. (3.66)
Это правило отбора относится к молекулам, не обладающим в нижнем электронном состоянии механическим моментом (преимущественно сюда относятся молекулы, находящиеся в -состоянии). Колебательные полосы таких молекул будут состоять из R-ветви, т. е. совокупности линий, для которых J = J' – J" = 1, и Р-ветви, т. е. совокупности линий, для которых J = J' – J" = –1.
Схема
переходов, дающих колебательно–вращательную
полосу для R-
и P-ветвей
в ИК-спектре поглощения, показана на
рис. 3.15.
Частоты
R-ветви
всегда расположены в коротковолновую
сторону от частоты
,
а частоты Р-ветви расположены с
длинноволновой стороны.
Выражая Е = Е'вн – Е''вн и частоты переходов в одних и тех же единицах (см–1), мы получим соответствующие формулы для R-ветви (J'– J" = 1)
,
(3.67)
или, выражая J'' через J' (J'' = J' – 1), получим
,
(3.68)
где J' = 1, 2, 3, ...(см. рис.3.15)
Аналогично получим, если произвести замену J' через J''(J'= J'' + 1)
, (3.69)
где J' = 0, 1, 2, 3, ...
Формулы
(3.68) и
(3.69), дают
ряд линий с частотами
которые при B'
=
B'',
были бы равноотстоящими, но в силу
наличия квадратичного члена с B'
B'
будут
сходиться. Если бы
B'
B'',
линии расходились бы. Для
колебательно-вращательных
спектров имеет место именно первый
случай
B'
B'',
так как '
''.
Аналогичную картину распределения линий вращательной структуры имеем для Р-ветви (J' – J'' = –1).
,
(3.70)
если выражать J' через J'' (здесь J'' = 1,2 , 3, ...). Можно получить и другую формулу
,
(3.71)
если;
выразить J''
через J'.
Формулы
(3.70) и
(3.71) также
дают ряд линий с
,
которые при B'
=
B''
были бы равноотстоящими, а в силу наличия
квадратичного члена с B'
B''
будут
расходиться (при B'
B''
они сходились бы). Проанализируем формулы
(3.68) и
(3.70), которые
подобны по своей записи, если J'
и J''
принимают
значения
1,
2, 3,
... Разница
этих формул состоит только в знаке
линейного члена. Если в формуле
(3.68) принять
J'
=
m
, где m
=
1,
2, 3,
...,
а в равенстве
(3.70) положить
J''
=
–m
, то обе
формулы становятся одинаковыми и их
можно записать в виде
, (3.72)
где
m
= 1, 2, 3,... для
R-ветви;
m
= –1, –2, –3,
...
для Р-ветви.
В соответствии со знаком m
часто R-ветвь
называют положительной, а Р-ветвь
– отрицательной
ветвью. Зная расстояния между линиями
P-
и R-ветвей,
можно по формулам (3.73) и (3.70) приблизительно
оценить вращательную постоянную, а
затем найти равновесное расстояние rе.
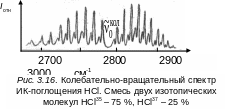
На рис. 3.16 приведен колебательно-вращательный
спектр ИК-поглощения молекулы НСl.
Применяя формулу
(3.72), нужно
всегда помнить, что m
> 0 соответствует
значению вращательного квантового
числа J
= J'
для верхнего колебательного уровня, a
m
<
0 –
значению квантового числа J
= J''
для нижнего,так что симметрия формулы
(3.72)
не является полной. на
рис. 3.16 линии R-ветви
расположены справа от колебательной
частоты
,
а Р-ветви
– слева. Нулевая линия
,
отсутствующая в колебательно-вращательном
спектре, соответствует случаю m
= 0.
В случае B'
= B''
формула
(3.72) упрощается
и принимает вид
.
(3.73
Выражение
(3.73) дает
равноотстоящие линии, симметрично
расположенные относительно чисто
колебательной полосы
.
В случае двухатомных молекул, у которых электронный момент количества движения не равен нулю, наряду с R- и Р-ветвью появляется Q-ветвь (нулевая) (J = J' – J'' = 0). Для Q-ветви получаем (J = J' = J'')
(3.74)
Так
как разность
(B'
– B'')
мала по сравнению с
B'
и
B'',
то линии
Q-ветви
расположены в длинноволновую сторону
от
(B'
B'')
и при малой дисперсии регистрируемого
прибора сливаются в одну узкую полосу.