3.4.2. Метод графической экстраполяции (метод Берджа – Шпонер)

Сущность метода графической экстраполяции заключается в том, что строится график зависимости колебательных интервалов E_{ + 1,}, от  + 1, который экстраполируется до пересечения с осью абсцисс. Площадь под этой кривой соответствует энергии диссоциации D_e. Заштрихованная область дает нижний предел . На рис. 3.12 приведен график этой зависимости для молекулы водорода.

При справедливости двучленной формулы для колебательной энергии (3.30), график является прямой линией и соответствующая площадь выражается формулой

. ( 3.51)

При небольших отступлениях от линейности получаются несколько иные значения диссоциации. Действительно, при линейной зависимости первой разности ордината в нулевой точке ( + 1), т. е. при  + 1=0, равна . В точке, для которой ордината обращается в нуль, значение абсциссы , как это следует из (3.41). Площадь треугольника определяется формулой , что согласуется с (3.42). Здесь энергию диссоциации отсчитывают от минимума потенциальной энергии. Реальную же энергию диссоциации D₀ следует отсчитывать от уровня  = 0, для которого нулевая энергия равна

,

а энергия диссоциации

D₀ = D_e – E_{0 .} (3.52)

Частоты переходов между соседними уровнями, как следует из (3.50), равны

, (3.53)

где отличается от на величину ангармоничности . Следовательно , т. е. величина практически совпадает с экспериментально измеряемой частотой

. ( 3.54)

При графическом определении энергии диссоциации D₀ нужно откладывать по оси абсцисс  + 1/2, а по оси ординат . Из формулы (3.50) получаем прежний график (прямую линию), что на рис. 3.12 только смещенный вправо на 1/2 (см. рис. 3.13).

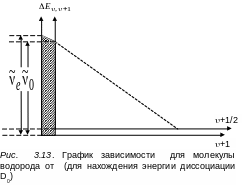
Разница значений и D₀ выражается площадью, заштрихованной на рис. 3.13. Оси абсцисс на рис. 3.13 совпадают. Действительно, при  + 1, согласно (3.35) а при согласно (3.50) . Заштрихованная площадь равна

(нулевая энергия).

Здесь учтено, что . Следовательно, площадь треугольника S_ в координатах и меньше площади другого треугольника на величину E₀. Итак, D₀ = D_e – E₀ или же

.

П олучаемые значения энергии диссоциации и D₀, рассчитываемые описанными выше методами, отличаются от истинных примерно на 15 %, что указывает на то, что формула Морзе, аппроксимирующая реальную кривую потенциальной энергии, является лишь грубым приближением. Экспериментальные точки ложатся не на прямую, а на кривую, которая загибается раньше, т. е. пересекает ось абсцисс при меньших значениях , чем это следует из анализа двучленной формулы (3.30). На рис. 3.12 и 3.14 показаны кривые зависимости E_+1, от квантового числа  для молекул H₂ и Li₂.

Энергия диссоциации определяется как площадь, ограниченная осями координат и реальной кривой, измеренная в соответствующем масштабе.

Энергию диссоциации можно измерить не только спектроскопическими, но и другими методами, которые мы здесь не рассматриваем (например, методом электронного удара, термическим или термохимическим. Знание энергий диссоциации молекул необходимо для термодинамических расчетов в химических реакциях.

Следует отметить, что задача определения энергии диссоциации по спектрам не проста, как может показаться из приведенного изложения. Требуется полная и точная расшифровка колебательного спектра, что не всегда можно довольно полно провести. Например, молекулы Н₂, N₂ и О₂ при обычных условиях не поглощают ИК-радиации (у них отсутствует дипольный момент). Колебательные частоты у аналогичных молекул получают из спектров КР или из ИК-спектров при высоких давлениях, когда при соударениях симметрия (D_h) молекулы нарушается и могут наблюдаться оптически неактивные полосы.