3.3.2 Уровни энергии, правила отбора и спектры двухатомной молекулы как ангармонического осциллятора

Потенциальная кривая гармонического осциллятора представляет собой симметричную параболу (см. рис. 3.4). Действительные потенциальные кривые двухатомных молекул асимметричны (см. рис. 3.2). Около минимума они близки к параболе, затем расширяются более быстро, чем парабола, и одна из их ветвей (правая) приближается к конечному пределу. Это приводит к тому, что расстояния между последовательными колебательными уровнями энергии не остаются постоянными, как для гармонического осциллятора, а постепенно уменьшаются (рис. 3.7). Колебательные уровни сближаются и сходятся по мере приближения к границе диссоциации.

На рис. 3.7 приведены колебательные уровни молекулы Н₂. Аналогичное схождение испытывают и уровни энергии других молекул.

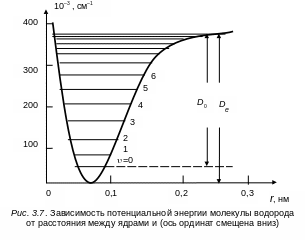
Сближение колебательных уровней с приближением к границе диссоциации связано с тем свойством уровней, что они располагаются тем теснее, чем шире потенциальная кривая. Для потенциальной кривой, имеющей форму параболы, мы имели равноотстоящие уровни энергии (см. рис. 3.5), причем расстояние между уровнями будет тем меньше, чем шире парабола. Для кривой, расширяющейся кверху быстрее параболы, уровни энергии будут постепенно сближаться ввиду того, что правая часть кривой Морзе приближается к конечному пределу, т. е. ширина кривой стремится к бесконечности при конечном значении энергии, происходит сгущение колебательных уровней энергии вблизи границы диссоциации. За границей диссоциации мы имеем непрерывную совокупность уровней энергии.

Следует отметить, что закон приближения кривой к пределу существен, так как от его характера зависит, получается ли вблизи границы бесконечное или конечное число колебательных уровней. Для молекулы Н₂ на рис. 3.7 число колебательных уровней конечно, получается всего лишь 15 уровней ( = 0, 1, …, 14). За уровнем  = 14 следует граница диссоциации.

Расположение колебательных уровней энергии двухатомной молекулы как ангармонического осциллятора мы можем получить, если в уравнение Шрёдингера (3.16) вместо потенциальной функции гармонического осциллятора подставим функцию Морзе. Решение уравнения Шрёдингера типа (3.16) с этой функцией дает следующее значение для колебательной энергии:

, ( 3.29)

где х – константа ангармоничности, по порядку величины равная . Эта формула наряду с основным членом, пропорциональным , содержит и поправочный член, пропорциональный и обусловленный ангармоничностью колебаний.

Если энергию, как и волновые числа, измерять в см^–1, то формулу (3.29) можно переписать, опустив постоянную Планка h:

. (3.30)

Как видно из выражения (3.30) , уровни энергии ангармонического осциллятора уже не являются равноотстоящими. Расстояние между соседними уровнями уменьшается с увеличением  до нуля, т. е. уровни энергии сходятся к некоторому пределу – границе диссоциации.

Чтобы получить спектр ангармонического осциллятора, необходимо знать населенность колебательных уровней энергии, вероятности переходов между ними и правила отбора.

Населенность уровней энергии подчиняется больцмановскому распределению

, (3.31)

а так как g_i = 1 для колебательных уровней энергии, то последняя формула (3.31) перепишется следующим образом:

, (3.32)

Здесь n_ – число частиц на колебательном уровне, характеризуемом колебательным квантовым числом , п₀ – число молекул на нулевом уровне энергии, k – постоянная Больцмана, а Т – температура среды. Не анализируя вероятности переходов (они определяются степенью перекрытия колебательных волновых функций) между колебательными уровнями энергии, приведем правила отбора для колебательного квантового числа . Возможны переходы в ИК поглощении и испускании, при которых колебательное квантовое число может изменяться на любую величину, т. е.

 = ' – '' = ±1 , ± 2, ± 3, . . . (3.33)

П ри этом возможны комбинации между различными колебательными уровнями энергии (как показано на рис. 3.8). Однако, учитывая тот факт, что при комнатной температуре преимущественно заселен только нижний колебательный уровень с  = 0, будем наблюдать переходы, идущие с нулевого колебательного уровня. На рис. 3.8 такие переходы в ИК-поглощении обозначены вертикальными сплошными стрелками.

Простой расчет показывает, что при комнатной температуре kТ  208,6 см^–1, а расстояние между колебательными уровнями, скажем, молекулы Н₂ составляет 4160 см^–1, то колебательный уровень с  = 1 заселен гораздо меньше, чем основной. Переходы с более высоколежащих уровней энергии на рис. 3.8 обозначены штриховыми стрелками. Эти переходы получили название «горячих», так как заметная заселенность их достигается только при более высоких (по сравнению с комнатной) температурах.

Для построения качественной картины спектра поглощения двухатомной молекулы проведем вычисление первых разностей ₁E_{ + 1, } между соседними уровнями энергии:

(3.34)

Анализ формулы (3.34) показывает, что разности энергий и частоты переходов    + 1 будут убывать линейно с увеличением . Для соответствующих переходов в ИК–спектре будем иметь следующие значения частот:

 E_{ + 1,},

0  1 ,

1  2 ,

2  3 .

При этом частота перехода – основная частота колебаний молекулы, получаемая из опыта, не будет совпадать с частотой гармонического осциллятора , определяемой формулой . Обозначив частоту гармонического осциллятора величиной т. е. частотой, определяемой из колебаний около положения равновесия, то формулу (3.34) можно переписать следующим образом:

. (3.35)

Частота перехода ' = 0  '' = 1 равна

, ( 3.36)

т. е. она меньше на величину удвоенного значения коэффициента при квадратичном члене в формуле (3.30), называемого постоянной ангармоничности.

Если вычислить разности между последовательными переходами, т. е. вторые разности ₂E = ₁E_{, – 1} – ₁E_{ + 1,} ,то они будут равны т. е. .

Как видим, вторые разности остаются постоянными при условии, что полная энергия Е_ выражается двучленной формулой (3.30).На рис. 3.9 приведены колебательные уровни энергии молекулы НСl, справа вычислены значения первых и вторых разностей между уровнями, слева в относительных единицах даны значения заселенностей колебательных уровней по отношению к нулевому уровню энергии.

Колебательный спектр молекулы НСl приведен на рис. 3.10 с учетом возможных переходов, обозначенных на рис. 3.8. Как видно, первый и второй обертоны быстро убывают по интенсивности по сравнению с основной частотой, поэтому часто не наблюдаются в ИК-спектрах.

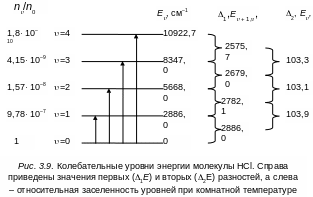
Наиболее важны в ИК-поглощении и комбинационном рассеянии переходы между нулевым ('' = 0) и возбужденными колебательными уровнями (' = 1, 2, 3, …). Соответствующие разности между нулевым колебательным уровнем и последующими будут иметь вид:

, (3.37)

где ' принимает целые значения, начиная с единицы. Если ' = 1, то мы получаем в поглощении основной тон:

(3.38)

Следует отметить, что при вычислении разностей уровней энергии , вначале идет более высокий уровень, из которого вычитается более низкий (например, ), но при обозначении частот поглощения между низким и верхним колебательными уровнями значение квантового числа нижнего уровня идет первым (например, ) и т. д.

При ' = 2 будем получать первый обертон

, (3.39)

при  = 3 имеем второй обертон,

, (3.40)

который по интенсивности много меньше основного тона (см. рис. 3.10).

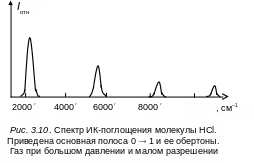
Благодаря отличию постоянной ангармоничности x_e от нуля (для НСl x_e = 0,0175) частоты обертонов не являются целыми числами, кратными основной частоте и, как правило, будут несколько меньше, чем . Интенсивность обертонов быстро убывает с увеличением ' (см. рис. 3.10), т. е. первый обертон значительно слабее основной частоты, второй значительно слабее первого и т. д. Чем меньше ангармоничность, тем быстрее происходит убывание интенсивности и, наоборот, при большой ангармоничности убывание становится более медленным и наблюдается большое число обертонов. Например, для молекулы НCl наблюдается три обертона основной частоты с заметной интенсивностью, показанной на рис. 3.10. Однако всегда надо помнить, что необходимым условием для поглощения ИК-радиации молекулой является изменение ее дипольного момента при колебаниях. Следовательно, все молекулы, в которых отсутствует дипольный момент и не возникает при колебаниях, не будут поглощать ИК-радиацию. Сюда относятся все молекулы, состоящие из одинаковых ядер (гомоядерные). Молекулы, состоящие из неодинаковых ядер (гетероядерные), обладают постоянным дипольным моментом, который изменяется при колебаниях, и будут поглощать ИК-радиацию.

В спектрах комбинационного рассеяния удается наблюдать лишь переходы 0 → 1, а обертоны, вследствие их малой интенсивности, отсутствуют. В табл. 3.1 приведены молекулярные постоянные ряда двухатомных молекул, полученные из колебательных спектров газов. Здесь же приведены значения силовых постоянных связей, рассчитанные по формуле для гармонического осциллятора. В последнем столбце присутствуют измеренные значения диссоциации (D₀) указанных молекул.

Таблица 3.1

Молекулярные постоянные некоторых двухатомных молекул

Молекула	Частота колебаний см–1	Постоянная ангармоничности см–1	Частота колебаний	Постоянная колебательно-вращательного взаимодействия см–1	Силовая постоянная k, н/м	Энергия диссоциации D0, эВ
1	2	3	4	5	6	7
Н2	4401	121	4160	3,062	575	4,178
НD	3817	92,5	3632	–	575,8	4,51
D2	3118	62,5	2993	–	576	4,56
НF	4139	90,0	3959	0,796	965	5,8
HСl	2991	52,5	2886	0,307	516,6	4,431
DСl	2145	27	2091	–	515,6	–
НВr	2649	45,2	2548,6	0,232	411	3,75
НI	2308	39,0	2230	0,169	313,4	3,06
JCl	384	1,50	381	0,536	240,4	2,152
N2	2359	14,3	2330,4	0,0173	2293	9,76
O2	1580	12,0	1556	0,0159	1175	5,12
NO	1904	14,0	1876	0,0178	1593	6,50
CO	2170	13,5	2143	0,0175	1902	11,09
F2	917	12,5	892	–	470	1,38
Cl2	560	2,7	554,6	0,00153	327	2,49
Br2	323	1,1	320,8	0,00032	245	1,97
J2	215	0,615	213,8	0,0113	172	1,54
Li2	351	2,55	346	0,6729	251	1,03