23.11. Черенковское излучение в эфире

В 1934 году П.А. Черенковым и С.И. Вавиловым был обнаружен особый вид излучения при наблюдении свечения раство-

сти света в данной среде, обгоняет своё собственное электромагнитное поле. В результате торможения электрона и возникает излучение. Позже было показано, что эффект Черенкова наблюдается и для протонов, релятивистских атомов железа и др.

Характерной особенностью черенковского излучения является направленность. Свет, излучаемый частицей, распространяется не во все стороны, а только в направлениях, составляющих

(345)

Согласно [203, с. 218], показатель преломления воздуха меняется как

Такой результат опровергает принятую в современной физике гипотезу о невозможности превысить скорость света. Но подтверждает теорию эфира, где скорость объекта, как и в других средах, может превышать скорость свободного распространения возмущений в эфире – скорость света.

Покажем, что при движении частицы в эфире формула (344) остаётся той же самой. Сжатие среды не может распространяться впереди движущегося объекта, так как в рассматриваемых условиях объект движется быстрее, чем световая волна. Поэтому фронт образующейся волны располагается за движущимся объектом. Каждая точка среды, мимо которой прошло тело, может

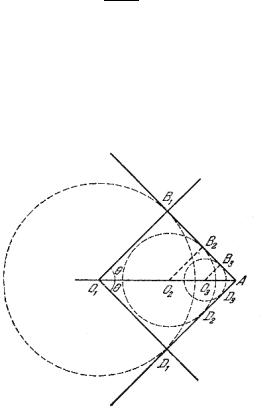
cos = 11 1 = .

Полученное для эфира значение cos совпадает со значением,

приведённым в формуле (344).

Огибающей1 1всех вторичных волн является коническая поверхность , см. рис. 29. Эта поверхность и является фрон-

том ударной волны.

Рис. 29. Фронт волны излучения.

В газовой динамике [9] при1 рассмотрении1 сверхзвуковых волн угол при вершине конуса называется углом при вершине конуса Маха. Величина конуса Маха в газодинамических экспериментах характеризует сверхзвуковые течения. В работах [81, с. 68; 204, с. 136] с помощью аналогичного подхода сделан вывод о том, что в экспериментах [205, 206] могли наблюдаться

629

сверхсветовые частицы, однако отсутствие в [205, 206] данных об углах излучения волн не позволило в явном виде оценить скорость частиц.

Вывод о наблюдении сверхсветовых частиц, помимо фунда-

измерения импульса частицы и угла излучения волн. Таким образом, значения всех известных масс сверхтяжёлых частиц требуют перепроверки в соответствующих дополнительных экспериментах. Скорее всего, массы будут уточнены.

23.12. Аномалии орбит первых спутников Фон Брауна

Интересные факты о ракете Jupiter-C, успешно запустившей первый американский спутник Explorer I в 1958 году, были опубликованы Р.К. Хоглендом (R.C. Hoagland) в статьях «Von Braun's 50-Year-Old-Secret. Parts 1 and 2», см., например: [327].

Аналогичные аномалии наблюдались в орбитах

спутников Explorer III и IV, а также трёх спутниках Vanguard. Расчёты Р.К. Хогленда959 [кмпоказали] , что превышение спутником

Explorer I апогея на не может быть объяснено большей

630

эффективностью многоступенчатых твёрдотопливных компонентов ракеты-носителя Jupiter-C, так как это потребовало бы увели-

чения на скорости всех верхних ступеней ракеты.

20%

Анализ исторических и инженерных фактов развития ракетной техники в США и СССР позволил Р.К. Хогленду сделать вывод о том, что причиной отклонения орбиты Explorer I были вращающиеся части ракеты Jupiter-C. Затем, ссылаясь на эксперименты Брюса де Пальмы с вращающимися телами, Р.К. Хогленд предложил качественную интерпретацию аномалий траектории с помощью концепции торсионного поля и добавления вращающемуся объекту и химическим реакциям свободной энергии из гиперпространства.

Здесь мы дадим другую интерпретацию аномалий на основе теории эфира, сделаем количественную оценку и сравниваем её со смещением орбиты Explorer I. Представленные результаты получены Ф.С. Зайцевым.

Ракета имела вращающуюся сборку в форме трубы, содержащей ступени 2 и 3. Вращение использовалось для компенсации дисбаланса тяги при сгорании отдельных топливных элементов этих ступеней. Четвёртая ступень имела один топливный элемент.

Линейная скорость вращения трубы есть , где –

Предположим, что в течение относительно длительного промежутка времени эта сила передаётся от эфира к трубе. Такое предположение даст оценку эффекта сверху, так как, возможно, трубе передаётся лишь часть возникающей в эфире силы.

зданного вращением трубы.

632

этот принцип обычно не верен для скоростей и траекторий. Из-за отсутствия подробных описаний движения ракеты Ju-

piter-C и модели, по которой прогнозировалась траектория, рассмотрим возмущение траектории ракеты только под действием силы . Такая оценка даст, конечно, лишь порядок величины возмущения.

Веса загруженных и порожних ступеней и хронометраж траектории даны в приведённых выше ссылках.

Труба раскручивалась до старта ракеты. Однако будем рас-

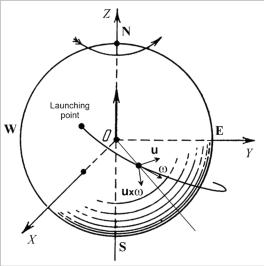
тяги – параллельна , см. рис. 30. Поэтому в упрощённом описании будем считать, что сила тяги ступени 4 не влияла

Рис. 30. Схема траектории подъёма ракеты. Тогда для смещения 4( 4) за время ( 23, 4] имеем

635

636

Скорость внешнего потока эфира через трубу может быть обусловлена совокупностью потоков эфира различного типа. Отметим, что среди них гравитационный поток эфира действует на вращающийся объект двояко: определяет его вес, взаимодействуя

предположений.

В дополнение к смещению в сторону космоса, вызванному силой , орбита расширялась также из-за ослабления силы тяготения с увеличением расстояния от Земли. Кроме того, есть исследования, например, Г.И. Шипова [доклад 25.04.2019 в РУДН], показывающие, что вращающийся объект теряет вес.

Учитывая все эти эффекты, можно сделать вывод о том, что представленная эфирная интерпретация согласуется по порядку

637

величины с наблюдаемым отклонением спутника на ~1000 [км] от ожидаемого в апогее положения.

Данный результат позволяет сделать важные выводы:

1.Получено ещё одно подтверждение существования потока эфира вокруг Земли, имеющего величину скорости (304).

2.Прогнозирование траектории вращающегося объекта в космосе при наличии внешнего потока эфира требует учёта обобщённой силы Жуковского. Её использование позволит выводить ту же массу на заданную орбиту при меньших затратах энергии.

3.Течение эфира вблизи Земли можно исследовать с помощью запуска двух простых одинаковых ракет со способной вращаться компонентой. Эта компонента не должна соприкасаться с воздухом, протекающим вблизи ракеты, во избежание возникновения эффекта Магнуса. В одной ракете компонента должна оставаться неподвижной, а в другой вращаться с большой скоростью, но только на некотором участке траектории. Разница в траекториях позволит оценить скорость течения эфира на том участке траектории, где компонента вращалась. В результате будет установлено соответствие между скоростью эфира и высо-

той над Землёй.

Более точное рассмотрение аномалий траектории потребовало бы знания подробной информации о потоке эфира, через который проходила вращающаяся труба, о конструкции ракеты Jupiter-C, в частности, её гироскопах и другом вращающемся оборудовании, а также знания деталей движения ракеты и модели, использованной для расчёта её траектории.

Представляется, что в настоящее время более реальным способом уточнённого анализа влияния обобщённой силы Жуковского на движение в космосе вращающегося объекта через поток эфира является проведение эксперимента, предложенного в пункте 3 выше.

638