Тогда (31) принимает вид

+ ∙ ( ) = 0,

что выражает закон

в эфире.

сохранения плотности заряда

Однако к сохранению заряда объекта есть

вопросы, см. п.18.15.

её малые возмущения – штрихом:

= + .

= , = + ,

декс « ».

В данном пункте для сокращения записи будем рассматри-

, опуская ин-

вать плотность эфира в механических единицах

Подставим данные представления в уравнения эфира (22),

= 0 имеем

(23). При отсутствии источников и внешних сил = 0, = 0,

+ ∙ ( + ′) ′ = 0,

106

+ ( ′

∙ ) ( + ′) ′ = −( + ′).

рого

=

=

,

и пренебрегая величинами вто-

Учитывая

порядка малости, получаем

+

∙ ′ = 0,

= −′.

В

′

′

)

выра-

предположении баротропности процесса

зим градиент давления через градиент

плотности′

=

(

′ = ′ ′

и воспользуемся формулой (19)

≈ ,

′

= ≈

2

следующей из уравнения состояния эфира. Тогда

= −

∙

,

= −

.

′

2

′

П

рым

/

и подставим в

родифференцируем первое уравнение по

него

из второго уравнения. Аналогично поступим

со вто-

уравнением′

. В результате исходная система распадается на

два уравнения

(

),

2

= ( ∙ ).

2

= ∙

2

′

2

′

107

∙

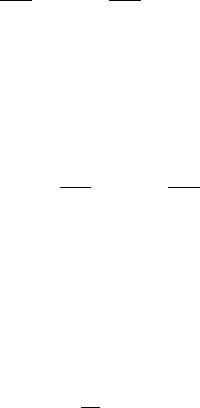
2

В первом уравнении возникает оператор Лапласа

. Правую часть второго уравнения преобразуем с

помощью

∆≡ ≡

формулы (5.5-19) из [51, с. 173]. Получим

2

=

∆

,

2

=

∆

+ × ( × ) .

2

′

2

′

′

типа, которое называется волновым уравнением или уравнением

′× ( × ) = 0

колебаний. Второе уравнение становится волновым уравнением

×

= 0

′

,

:

при

например, в случае безвихревого течения

× ( × ′) = 0

2

′

2

′

(78)

стью

или вихревого течения с безвихревой завихренно-

Волновое

2

= ∆ ,

2

= ∆ .

уравнение достаточно хорошо изучено (см., напри-

вые решения и без предположения о малых возмущениях иско-

нений (22), (23), (15) = 0

= 0 = 0

мых функций.

Например, при

,

,

одним из решений урав-

+

∙

( ) = 0

(79)

+ ( ∙ )( ) = −

2

)

= − ,0

(

при

= являются

108

плоские волны

,0

( , ) = ±

−

−

2

,

(80)

1

1

,0

( , )

= 1 − ,0

,

имеющие поперечную и продольную к оси

составляющие.

стемы

,

,

– постоянная скорость. Произвольная диф-

Здесь

– единичные базисные векторы

декартовой си-

ференцируемая

,0

координат,

( , )

1 − ( 1

)

≥ 0

Интересно отметить, что для

функция

и произвольная константа

должны

, то есть эта волна удовлетворяет и макроуровневым (4)– =

удовлетворять условию

существования

:

1

2

.

1

рассматриваемой волны

(6), и

микроуровневым (1)–(3) уравнениям эфира.

0

Согласно формулам (20) и (21), данному решению соответ-

волны при

,0

ствуют плоские электромагнитные волны. При этом продольная

компонента

скорости

выпадает

из

электромагнитной

дифференцировании

по пространственным пере-

менным. В результате при

описании волн в терминах векторов

и выпадает составляющая движения в направлении распро-

странения волны.

Эфирное представление электромагнитных волн позволяет

вой дуализм. Корпускулярное воздействие можно отнести к про-

,0

явлению продольной компоненты скорости волны (компоненты

в рассмотренном примере и

в формуле (238)), а волно-

вые эффекты – к проявлению поперечной компоненты скорости.

системе координат

с

=

,

Приведём пример волнового решения системы (79), в кото-

,

одним из

( , , )

. В сферической

ром не используется предположение

единичными базисными векторами

приближённых решений уравнений (79) при

больших

является сферическая волна

109

2

2 3

22

(81)

где

2

3

( − 2 )

= ± ( − 2 )

− 2 ,

и

– произвольные константы, обеспечивающие неотри-

цательность выражения под корнем.

Рассчитав волновые плотность и скорость эфира, можно с по-

выми, так как операция

мощью формул (20) и (21) найти соответствующие им электриче-

ское и магнитное поля

и . При этом

и также будут волно-

дифференцирования не меняет волновой

ного происхождения, приводит к трудно воспринимаемым пара-

доксам, таким как корпускулярно-волновой дуализм.

Отметим, что с помощью задания источников и внешних

сил в уравнениях (22), (23) можно получить эфирные

волны

достаточно сложной структуры, в том числе описываемые в тер-

минах

и как продольные электромагнитные волны. Подроб-

ный

обзор и анализ экспериментальных наблюдений продоль-

ных электромагнитных волн дан в книге [63].

Из опытов известно, что скорость свободного распростране-

ния волн в эфире равна скорости света

. Поэтому в волновых

уравнениях для малых возмущений (78)

и в решениях (80), (81)

более общей системы (79) можно положить

,

,

. В самом общем случае, например

при сильных возму-

| | =

,0 =

щениях или наличии препятствий, источников или стоков, внеш-

| 2| =

них сил, скорость

и плотность эфира, в том числе и для вол-

необходимо рассчитывать с помощью исход-

новых процессов,