
- •Предисловие к первому и второму изданиям
- •Предисловие к третьему изданию
- •Правовые вопросы
- •1. Иерархия математических моделей эфира как сплошной среды
- •1.1. Микроуровневая и макроуровневая модели эфира
- •1.2. Сравнение уравнений эфира с классическими уравнениями механики сплошной среды
- •1.3. Инвариантность уравнений неразрывности и движения эфира относительно преобразования Галилея
- •1.4. Плотность энергии, плотность мощности эфира. Давление эфира. Уравнение состояния эфира
- •2. Вывод уравнений Максвелла из уравнений эфира
- •2.1. Вывод обобщённых уравнений Максвелла – Лоренца из уравнений эфира
- •2.2. Вычисление электрического и магнитного полей
- •2.3. Векторный потенциал. Физическая интерпретация
- •2.4. Обобщённые уравнения колебаний электрического и магнитного полей
- •2.5. *Изучение вопроса об инвариантности обобщённых и классических уравнений Максвелла при преобразовании Галилея
- •2.5.2. Преобразование производных и операторов при замене переменных Галилея. Инвариантность уравнений неразрывности и движения эфира в эйлеровых переменных
- •2.5.3. Причина потери галилеевой инвариантности в обобщённых уравнениях Максвелла – неинвариантное преобразование исходных уравнений эфира. Инвариантность обобщённых уравнений Максвелла при досветовой скорости движения системы координат
- •2.5.4. Галилеева неинвариантность классических уравнений Максвелла в отсутствие среды и их инвариантность в эфирной трактовке при досветовой скорости движения системы координат
- •2.6. Общие замечания
- •3. Заряд, его электрическое поле. Теорема Гаусса. Закон Кулона. Электрический потенциал. Связь потенциального электрического поля с градиентом давления эфира. Сохранение заряда
- •4. Волновые процессы в эфире
- •4.1. Уравнения малых колебаний эфира. Некоторые волновые решения исходных уравнений эфира
- •4.2. Непригодность квантовой механики для полноценного описания природы
- •4.2.1. Анализ основ квантовой механики с позиций методологии математического моделирования
- •4.2.2. Вывод уравнения Шрёдингера из уравнений эфира. Эфирная интерпретация волновой функции. Ошибочность отождествления частицы и волны
- •4.2.4. Неадекватность интерпретации экспериментов, якобы обосновывающих квантовую механику
- •4.2.5. Основные выводы
- •5. Энергия электромагнитного поля
- •5.1. Общие формулы для плотностей энергии и мощности электромагнитного поля
- •5.2. Плотность энергии электромагнитной волны
- •5.3. Интерпретация энергии кванта света, постоянной Планка, волны де Бройля
- •6. Разрывы в эфире. Эффекты квантования
- •6.1. Самопроизвольное формирование разрывов
- •6.2. Условия на поверхности разрыва
- •6.3. Пример квантования
- •6.4. Эфирное представление условий разрыва магнитного и электрического полей
- •7. Вывод закона Био – Савара из уравнений эфира
- •9. Основной закон электромагнитной индукции. Электродвижущая сила. Правило Ленца
- •9.1. Основной закон электромагнитной индукции
- •9.2. Галилеева инвариантность основного закона электромагнитной индукции
- •10. Вихревое движение
- •10.1. Замкнутая вихревая трубка как основная устойчивая структура вихревого движения эфира
- •10.2. Вихревой импульс эфира. Закон сохранения вихревого импульса. Сохранения момента магнитного поля
- •11. Внешняя сила, действующая со стороны среды на завихренное течение эфира. Обобщение силы Жуковского для случая трёхмерного частично или полностью проницаемого объекта
- •11.1. Обобщение силы Жуковского
- •11.2. Движение элементарного объёма эфира в сильных внешних магнитном и электрическом полях. Ларморовский радиус вращения элементарного объёма эфира. Циклотронный эфирный резонанс
- •12. Электрический ток в проводниках
- •12.1. Токи вне и внутри проводников. Законы Ампера
- •12.2. Закон Ома. Электрическая проводимость
- •12.3. Закон Джоуля и Ленца
- •12.4. Влияние распределения скорости эфира внутри провода на создаваемое в нём магнитное поле и плотность электрического тока
- •12.5. Сверхпроводимость
- •13. Силовое воздействие эфира на объект, вызванное наличием градиента давления
- •14. Эфирный аналог теоремы Бернулли. Эффекты, обусловленные уравнением состояния эфира
- •14.1. Теорема Бернулли в эфире. Сравнение интеграла Бернулли с уравнением состояния эфира
- •14.3. Механизм воздействия обобщённой силы Жуковского
- •14.4. Принцип перемещения в эфире без отбрасывания количества движения
- •14.5. Плотность кинетической энергии эфира в электроне и протоне. Технологии, основанные на превращении осязаемой материи в поток эфира. Эфиробарический боеприпас
- •15. Классификация установившихся потоков эфира
- •15.1. Электрический поток эфира
- •15.2. Гравитационный поток эфира
- •15.3. Магнитный поток эфира
- •16. Силовое воздействие потока эфира на объект
- •16.1. Воздействие на заряженный объект. Сила Лоренца
- •16.2. Сила эфирного гравитационного притяжения. Гравитационная и инертная массы
- •17. Взаимодействие объектов
- •17.1. Закон Кулона для двух заряженных объектов
- •17.2. Закон гравитационного тяготения
- •18. Эфирная трактовка в электротехнике и электрохимии
- •18.1. Создание электрического тока в проводе. Падение напряжения на участке цепи
- •18.2. Мощность электрической цепи
- •18.3. Электрическое сопротивление в электрохимической ячейке и газовом разряде
- •18.4. Электрическое сопротивление в проводе
- •18.5. Электроёмкость, конденсаторы
- •18.6. Уравнение тока в контуре постоянной формы
- •18.8. Магнитная энергия замкнутого проводника с током в магнитном поле. Плотность магнитной энергии в цепи
- •18.9. Полная электромагнитная мощность цепи с током. Вектор Умова – Пойнтинга
- •18.10. Взрыв проволочек электрическим током в вакууме. Взрывная электронная эмиссия
- •18.11. Э.д.с. Жуковского. Униполярный генератор
- •18.12. Эффект Холла. Постоянная Холла
- •18.13. Электростатические эффекты
- •18.14. Электростатические устройства
- •18.15. Эксперимент для проверки закона сохранения заряда объектом на длительном промежутке времени
- •18.16. Удержание плазмы в тороидальных ловушках. Обобщение математических моделей плазмы
- •19. Интерпретация магнитных явлений
- •19.1. Потоки эфира, создаваемые доменом и постоянным магнитом
- •19.2. Магнит и ферромагнитный материал
- •19.3. Проводящий немагнитный материал и магнит
- •19.4. Проводник с током и магнит
- •19.5. Взаимодействие магнитов друг с другом
- •19.6. О попытках создания двигателя или генератора энергии на основе перемещения системы постоянных магнитов
- •20. Оценка плотности невозмущённого эфира
- •20.1. Единицы измерения плотности эфира
- •20.2. Оценки на основе экспериментов с лазерами
- •20.3. Оценки с использованием эфирной модели фотона и характеристик электромагнитного поля в нём
- •20.4. Оценка из эфирной модели фотона и его импульса
- •20.5. Оценки с применением эфирных моделей электрона и протона
- •20.6. Оценка на основе данных о кулоновском барьере
- •20.7. Основные выводы. Значение плотности эфира
- •20.8. Ошибочность принятия диэлектрической проницаемости вакуума в качестве невозмущённой плотности эфира
- •21. Структура носителей эфира – ньютониев. Кинетические эффекты в эфире и веществе
- •21.1. Давление невозмущённого эфира
- •21.2. Масса и размер носителей эфира – ньютониев. Среднее расстояние между ними
- •21.3. Распределение ньютониев при хаотическом тепловом и направленном движении
- •21.4. Краткий обзор моделей неравновесных, необратимых процессов и коэффициентов переноса в физике. Применение к описанию кинетики ньютониев
- •21.5. Теплопередача в эфире. Теплоёмкость эфира
- •21.6. Теплопередача в твёрдом веществе
- •21.7. Вязкость эфира
- •21.8. Самодиффузия в эфире
- •21.9. Электрическая проводимость эфира и вещества при отсутствии свободных зарядов
- •21.10. Оценка параметров эфирной модели электропроводности по опытным данным
- •21.11. Закон Видемана и Франца в металле и эфире
- •21.12. Давление эфира внутри твёрдых материалов и жидкостей
- •21.13. Слипание пластин с гладкой поверхностью, эффект Казимира. Фазовый переход состояний объектов. Радиоактивный распад
- •21.14. Явления в контактах
- •21.15. Электроотрицательность химических элементов
- •21.16. Плотность тока эфира в газовом разряде
- •21.17. Нецелесообразность применения понятия термодинамической энтропии в модели эфира
- •22. Оценка радиусов пограничных слоёв, обуславливающих возникновение силы Лоренца и силы гравитации
- •22.1. Заряженные объекты
- •22.2. Объекты, обладающие массой. Оценка скорости вращения гравитационного потока эфира вокруг Земли, его градиента давления и давления
- •23. Сводка экспериментальных фактов, подтверждающих наличие эфира
- •23.1. Основные общие законы электродинамики и гравитации
- •23.2. Электрический ток в проводе
- •23.2.1. Внутренняя противоречивость модели свободных электронов в твёрдом проводнике
- •23.2.2. Проблемы интерпретации опытов в электронной теории проводимости
- •23.2.3. Расчёт течения эфира внутри провода
- •23.3. Эксперименты с униполярным генератором. Эффект Аспдена
- •23.5. Теплопроводность металлов
- •23.5.1. Теплопроводность в поле силы тяготения
- •23.5.2. Теплопроводность во вращающемся диске
- •23.5.3. Теплопроводность при наличии вибрации
- •23.6. Вращение тел при отсутствии внешнего магнитного поля
- •23.6.1. Опыт Толмена и Стюарта с вращающейся катушкой
- •23.6.2. Инерционный опыт Лепёшкина с вращающейся спиралью
- •23.6.3. Создание магнитного поля вращающимся сверхпроводником, ферромагнетиком и другими объектами. Момент Лондона. Эффект Барнетта. Гравитомагнитный момент Лондона
- •23.6.4. Создание в эфире фантома вращением магнитного диска
- •23.6.5. Электромагнитное поле, создаваемое камертоном
- •23.6.6. Магнитное поле вращающегося немагнитного диска. Проект экспериментов
- •23.6.7. Опыт с вращающимся диском и флюгером
- •23.6.8. Ошибочные трактовки движения объектов в некоторых опытах как результата механического взаимодействия с эфиром
- •23.7. О разрушении материала вращением
- •23.8. Разрушение материала лазером
- •23.9. Эксперименты в техническом вакууме
- •23.9.1. Темновой ток
- •23.9.2. Темновой ток в присутствии магнита
- •23.9.3. Мельничка
- •23.9.4. Коловрат
- •23.9.6. Автоэлектронная эмиссия и фотоэмиссия электронов из проводника
- •23.9.7. Пробойный ток
- •23.10. Противодействие гравитации. Экранировка гравитационного потока эфира и его изменение
- •23.10.1. Вращение частично сверхпроводящего керамического диска в магнитном поле. Противодействие гравитации в эксперименте Подклетнова
- •23.10.2. Уменьшение веса электрона в вакуумной трубке, окружённой сверхпроводником, за счёт экранировки гравитационного потока эфира
- •23.10.3. Эксперименты В.В. Чернова по изменению силы тяжести. Создание фантомов в эфире вращающимся стальным маховиком, электрическим током и крутящимся магнитом
- •23.10.4. Экранировка гравитационного потока эфира атомарным порошком
- •23.10.5. Проект стенда для опытов с гравитацией
- •23.11. Черенковское излучение в эфире
- •23.12. Аномалии орбит первых спутников Фон Брауна
- •23.13. Эфирная интерпретация принципа работы электродвигателя на подшипниках
- •23.13.1. Простейшая эфирная модель электродвигателя на подшипниках
- •23.13.2. Анализ эфирной модели
- •23.13.3. Выводы и перспективы применения
- •23.14. Странное излучение, наблюдаемое при низкотемпературных ядерных реакциях (LENR)
- •24. Эфирная модель шаровой молнии
- •24.1. Аномальные свойства ШМ
- •24.2. Попытки объяснения ШМ без учёта эфира
- •24.3. Простейшая эфирная модель ШМ. Трактовка аномальных свойств
- •24.4. Интерпретация экспериментов Теслы с ШМ. Резонансный механизм аномальных явлений в электротехнических устройствах
- •25. Эфирная модель строения Земли
- •26. Информационная составляющая биологических систем и её проявления
- •27. «Путешествия» во времени
- •Заключение
- •Приложение 1. Вывод уравнения Ампера
- •Приложение 2. О поисках эфирного ветра
- •Приложение 3. О движущихся источниках света
- •Приложение 4. Траектории лагранжевых частиц для уравнения движения с нулевой правой частью
- •Приложение 5. Новые системы единиц измерения, связанные с эфиром
- •Приложение 6. Концентрации электронов и ионов в воздухе при низком давлении
- •Приложение 7. Ионный ветер в коронном разряде
- •Литература
- •Литература, добавленная во 2-м издании
- •Литература, добавленная в 3-м издании
- •Представления некоторых великих учёных об устройстве материи
- •Цитаты из высказываний об изданиях книги
- •Фальсификации, искажения, непонимание методологии и результатов книги
• не способна прогнозировать методы решения насущных проблем человечества (пп. 10).
Перечисленные серьёзные недостатки приводят к скептическому отношению многих учёных к КМ.
Однако в п. 4.2.2, 4.2.3 показано, что теория эфира отчасти реабилитирует результаты КМ, позволяет дать физическую интерпретацию волновой функции, найти пределы применимости уравнения Шрёдингера, устранить парадоксы КМ и избежать наделения явлений природы противоречивыми свойствами. Кроме того, п. 4.2.2 демонстрирует ошибочность утверждения квантовой механики (см., например: [253, с. 39]) о невозможности вывода уравнения Шрёдингера из подходов классической физики.
4.2.2.Вывод уравнения Шрёдингера из уравнений эфира. Эфирная интерпретация волновой функции. Ошибочность отождествления частицы и волны
В данной книге показано, что принятие во внимание наличия эфира (среды, в которой происходят все процессы) позволяет вывести математически все основные экспериментальные законы физики из двух простых посылок, снять практически все парадоксы современной физики и понять законы и механизмы явлений, которые физика отказывается объяснять. Это показывает большу́ю общность эфирной модели природы и обосновывает возможность анализа с её позиций менее общих моделей.
Дадим эфирную трактовку КМ. В пп. 6 п. 4.2.1 отмечена газогидродинамическая интерпретация КМ, полученная из уравнения Шрёдингера. Здесь мы поступим в некотором смысле наоборот, выведем уравнение Шрёдингера из уравнений эфира (4)–(6).
На с. 39 установлено, что уравнения эфира применимы для описания микромира. Поэтому использование уравнений эфира для анализа КМ корректно.
121
КМ принимает уравнение Шрёдингера как постулат, но пытается различными способами объяснить причину выбора именно этого уравнения, так как в качестве постулата можно было бы взять любое уравнение. Например, в [30, п. 21] строится уравнение, которое обращается в тождество на плоской волне де Бройля и удовлетворяет ещё ряду требований. В [254, п. 8] применяется оператор полной энергии частицы. В [253, с. 39, 40, 52] (или [251(c)]) стационарное и нестационарное уравнения Шрёдингера выводятся из уравнения колебаний.
Какой бы ни был подход к обоснованию выбора в КМ уравнения Шрёдингера среди других уравнений, проведение рассужде-
ний [253, с. 39, 40, 52] в обратную сторону, от уравнения Шрёдин-
гера к уравнению колебаний, показывает связь построенного в других подходах уравнения Шрёдингера с уравнением колебаний.
Физическое содержание этой связи сформулировано в последнем абзаце данного пункта после её подробного рассмотрения.
Итак, выкладки [253, с. 39, 40, 52] устанавливают связь стационарного и нестационарного уравнений Шрёдингера с хорошо известным явлением колебаний различных физических систем. Эти выкладки используют стандартный подход математической физики к изучению установившихся монохроматических колебаний [62, гл. VII, п. 1]. Фактически единственным неформальным шагом в [253, с. 39, 40, 52], требующим интерпретации, является замена длины монохроматической волны в среде на длину волны де Бройля. Относительно высокая математическая строгость подхода [253, с. 39, 40, 52] обуславливает его выбор для построения эфирной интерпретации уравнений Шрёдингера.
Интересно, что достаточно общий способ построения КМ [253, с. 39, 40, 52] не вошёл в известные нам более поздние учебники, даже в учебник тех же авторов [258, п. 2]. Такое положение, видимо, связано с явно напрашивающейся аналогией распространения волны в КМ, как и обычной волны, в некоторой
122
среде, а это невозможно в концепции пустого пространства теории относительности.
Рассуждения [253, с. 39, 40, 52] начинаются с рассмотрения абстрактного уравнения колебаний. В теории эфира уравнение колебаний является следствием исходных уравнений эфира и описывает колебания малых возмущений плотности и/или скорости эфира, см. п. 4.1 и формулу (78). Сильные возмущения (и другие эффекты) могут приводить к нелинейности, поэтому сравнивать исходные нелинейные уравнения эфира (4)–(6) с линейным уравнением Шрёдингера не имеет смысла.
Повторение без изменений выкладок [253, с. 39, 40, 52], исходя из уравнения колебаний скорости эфира, позволяет установить эфирную интерпретацию уравнений Шрёдингера и волновой функции. Повторим эти выкладки, аккуратно отслеживая на каждом шаге эфирную интерпретацию преобразований.
В эфирной модели природы частица движется не в пустоте, а в среде (эфире). Рассмотрим в этой среде монохроматическую волну
стваΨ( ) |
ReΨ( ) |
+ ImΨ( ) , |
|
(82) |
||||||
|
|
|
|
|
|
|
|
|
||
является плоской [263], здесь |
|
Ψ( ) = Ψ0exp(−) |
|
|
|
|||||
где |
|
– комплексная функция точки трёхмерного простран- |
||||||||
|
вещественных чисел. При |
|
волна (82) |
|||||||
|
Подчеркнём, |
= 2 |
|
– волновой вектор, направление |
||||||
которого перпендикулярно |
|
фазовому фронту бегущей волны, |
|
|||||||
|
|
|
|
|
|
|
||||
– круговая частота |
|
|
, – частота колебаний волны. |
|
||||||
что комплексная форма представления волны
(82) используется в математике и математической физике только для краткой записи одновременных выкладок с двумя вещественными функциями, содержащимися в вещественной( , (дей) - ствительной) и мнимой частях комплексной функции . В приложениях теории функции комплексного переменного к решению практических задач в вещественном пространстве всегда
123
аккуратно отслеживают эквивалентность преобразований с комплексными функциями и способ возврата к исходным вещественным функциям, см., например: [140, гл. 3]. Иначе результат может не иметь отношения к решению исходной задачи. Например, если нелинейное уравнение, сформулированное в вещественном пространстве, преобразовать с помощью замены искомой функции на комплексную, то вещественная и/или мнимая часть решения преобразованного уравнения может, вообще говоря, не удовлетворять исходному уравнению.
Рассмотрим в (78) уравнение для вектора скорости. КМ описывает процессы двумя скалярными функциями вещественной и мнимой частью волновой функции. То есть рассматривает двумерные задачи. Поэтому из трёх уравнений для компонентов вектора скорости (78) используем только две. Получив из них с помощью (82) другое уравнение, которому удовлетворяет волна (82), увидим, что оно совпадает с уравнением Шрёдингера. Это даст эфирную интерпретацию уравнения Шрёдингера и волновой функции. Отметим, что данный способ построения КМ позволяет обобщить её на трёхмерное уравнение Шрёдингера для волновой функции, имеющей три компоненты.
Подставим вещественную и мнимую части (82) в уравнение (78) для двух компонентов скорости и запишем их в кратком виде с помощью комплексной функции. ΨПолучаем( ) уравнение колебаний малых возмущений амплитуды скорости монохроматической волны в эфире
∆Ψ( ) + |
2 |
|
(83) |
2 |
Ψ( ) = 0. |
|
|
|
|
|
|
Из вывода уравнения (78) видно, что скорость распространения (19) колебаний скорости может зависеть от точки в пространстве, но не должна зависеть от времени.
124
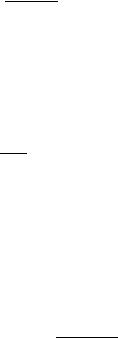
Согласно (82), величина |
|
|
≡ |
|
(84) |
имеет смысл длины волны. |
/(2 ) |
|
Заменяя в (83) отношение двух параметров на один, получим уравнение колебаний малых возмущений амплитуды скорости
монохроматической волны в следующей форме |
|
∆Ψ( ) + 2 Ψ( ) = 0. |
(85) |
Вуравнении (85) длина волны является входным параметром, который по способу построения второго уравнения в (78) может быть функцией точки пространства, но не должен зависеть от времени.
ВКМ процессы характеризуются длиной волны де Бройля,
которая вводится как (см, например, обзор [251(f)]) |
|
|||||||||||||
|
|
дБ ≡ 0 |
= 0 = |
|
/(20 ) |
, |
(86) |
|||||||
|
– полная энергия |
|
0 |
|
|
|
|
|
|
|
||||
= |
|
|
|
|
|
и |
|
|
|
|
|
|
||
где |
– постоянная Планка, |
|
|
|
– масса и скорость частицы, |
|||||||||
энергий |
|
частицы, |
|
|
– частота колебаний. |
( ) |
||||||||
|
|
|
0 /2 |
|
|
|||||||||
По закону сохранения энергии полная энергия частицы рав- |
||||||||||||||
на также сумме кинетической |
|
|
|
|
2 |
и потенциальной |
|
|||||||
|
|
2 |
+ ( ) = |
= . |
|
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
В [253, с. 39] в уравнении колебаний (85) заменяется на дБ.
Рассмотрим обстоятельно эфирную интерпретацию такой замены, так как она придаёт другой смысл уравнению колебаний
амплитуды скорости эфира. |
|
|
|
|
|
|
|
|
|
|||
|
Исходное уравнение колебаний скорости эфира (78) описы- |
|||||||||||
скорость |
|
может меняться, |
|
|
|
|
= / , |
|
|
|
||
вает среду, в которой волна распространяется во всём простран- |
||||||||||||
под |
|
|
|
|
|
: |
2 |
|
|
(19). При этом |
||
стве с характерной скоростью |
|
|
|
|||||||||
|
|
|
|
как и в других средах, в том числе |
||||||||
|
действием движущегося в среде объекта. |
|
|
|
||||||||
|
Согласно (84), (86), подстановка |
|
вместо |
|
|
заменяет ис- |
||||||
ющей свойства частицы, а не |
|
|
,дБ = /( 0 ) |
|
|
|||||||
ходную среду на другую, в которой |
волна распространяется во |
|||||||||||
дБ |
|
|
|
|||||||||
всём пространстве со скоростью |
|
|
|
|
, характеризу- |
|||||||
среды. Происходит отождествление частицы со всей средой, в которой она движется, и подмена
во всём пространстве характеристики среды |
| | |
на характери- |
||||||
дённой |
|
( ) = 0 |
. |
|
,дБ |
|
||
стику частицы |
|
|
|
|
||||
При |
|
,дБскорость распространения волны |
|
во ве- |
||||
стицы |
,дБ = /( 0 ) = /2. В принципе, волна может дви- |
|||||||
|
данной заменой новой среде равна половине скорости ча- |
|||||||
гаться медленнее объекта, например, пуля, летящая быстрее скорости звука, создаёт в воздухе волну, движущуюся со скоростью звука. Однако данный результат показывает, что КМ не описываетчастицу, так как частица не может/2 двигаться одновременно с двумя разными скоростями и .
С точки зрения теории эфира основная некорректность КМ состоит в стирании во всём пространстве различия между частицей и средой, в которой эта частица движется. Стирание различия происходит даже в том месте, куда возмущение среды от движения частицы ещё не дошло. Однако КМ не может поступить по-другому, так как принимает концепцию пустого пространства и вынуждена заполнить частицей всё пространство.
126

В теории эфира свойства объекта и среды, в которой он находится, различаются. Именно отличие свойств выделяет объект в среде. Поэтому эфирная интерпретация позволяет| | принять за-мену,дБ скорости распространения волны в эфире на скорость лишь в некоторой малой окрестности вне частицы, а не во
всём пространстве, и то с большой натяжкой, как редкий частный случай. Если такая замена скоростей не имеет отношения к реальности даже в некоторой малой окрестности частицы, то интерпретация КМ заканчивается на данном этапе неутешительным для КМ выводом: даже в самой общей, на настоящий момент, эфирной модели природы КМ не имеет интерпретации.
Далее подход [253, с. 40] исключает скорость |
|
в законе со- |
|||||||||
хранения энергии частицы с помощью формулы |
(86) и устанав- |
||||||||||
|
|
|
|||||||||
ливает связь дБ с полной и потенциальной энергиями |
|||||||||||
|
2 0 2дБ |
+ ( ) = , |
|
|
|
||||||
|
12 |
= |
2 20 |
|
− ( ) , |
|
|
|
|||
дБ |
|
|
|
|
|
|
|
|
|
||
4 2 |
= |
2 0 |
− ( ) , |
|
|
|
|||||
|
2 |
|
|
2 |
|
|
|
||||
дБ |
|
|
|
|
|
|
|
|
|
||
= /(2 ) |
|
|
|
|
|
|
|
|
|
|
|
– приведённая постоянная Планка. |
|
|
|
||||||||
Подстановка данного выражения в (85) приводит к уравне- |
|||||||||||
нию для амплитуды колебаний |
|
малых возмущений скоро- |
|||||||||
сти эфира, создаваемых в |
некоторой своей малой окрестности |
||||||||||
|
|
Ψ( ) |
|
|
|
|
|||||
частицей массы 0, движущейся со скоростью : |
|
|
|||||||||
∆Ψ( ) + |
20 |
− ( )Ψ( ) = 0. |
|
|
(87) |
||||||
127

скорости эфира = = |
полная волна малых возмущений |
||||||||||||||||||
С учётом |
(82) есть |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(88) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
+ 2 0 ∆ ( , ) − ( ) ( , ) = 0. |
|
(89) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
128 |
|
|
|
|
|
Уравнение (87) совпадает со стационарным уравнением |
|||||||||||||||||||
Шрёдингера. Это уравнение принимается в КМ как постулат для |
|||||||||||||||||||
нахождения волновой функция |
|
|
, физический смысл которой |
||||||||||||||||
КМ не может установить в своей методологии. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ( ) |
|
|
|
|
|
Нестационарное уравнение Шрёдингера выводится из ста- |
|||||||||||||||||||
ционарного (87) исключением |
|
с помощью формулы (88), см. |
|||||||||||||||||
[253, с. 52] или [251(c)]. Продифференцируем |
(88) по |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
Ψ( ) , |
|
|
|
||||||
|
|
|
|
|
|
( , ) = |
( , ), |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
− ( , ) = ( , ). |
|
|
|
|||||||||||||
Умножая (87) на |
|
|
|
и подставляя в него производную по |
|||||||||||||||
времени вместо |
|
|
|
|
|
/ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
, приходим к уравнению |
|
|
|||||||||||
− |
|
( , ) |
|
|
|
|
|
|
|
||||||||||
Знак « |
» в |
первом члене появился из-за рассмотрения |
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
процессов. |
|||||||
в (82), как−это обычно делается в теории волновых |
|
+ |
|||||||||||||||||
Операция комплексного сопряжения переводит это уравнение к принятому в КМ виду
Данное уравнение получено для монохроматической волны, не обязательно плоской. Переход( , )от него к уравнению для волновой функции общего вида , которая уже может и не быть монохроматической волной, совершается с использованием разложения по собственным функциям стационарного уравнения
Вкачестве собственных значений уравнения (87) рассматриΨ( )- ваются значения энергии . Соответствующие им решения называются собственными.
Задача на собственные значения является достаточно сложной. Теоремы о её решении можно найти, например в [51, п. 15.4.-12, 15.4-6], см. также [253, с. 41–43]. В общем случае множество собственных значений может быть как дискретным, так
инепрерывным. Теорема разложимости в ряд по собственным функциям краевой задачи о колебании ограниченных объёмов сформулирована, например в [62, гл. V, п. 3.1].
ВКМ уравнение (87) рассматривается во всём пространстве. Теоремы о единственности решения задачи о колебаниях в неограниченной области приведены в [62, гл. VII, п. 3]. Поиск собственных значений в КМ обычно проводится для конкретных потенциалов U. Общие теоремы сформулированы в [264, п. 6–9].
Если у задачи для уравнения (87) существует дискретноемножество (конечное или бесконечное) собственныхΨ (значений)
,которым соответствуют( , ) собственные функции такие, что функция может быть представлена в виде ряда (ко-Шрёдингера (87) [253, с. 52].
нечного или бесконечного) |
|
|
|
|
( , ) = Ψ ( ) − / |
(90) |
|||
|
|
, то |
( , ) |
также является ре- |
шением той же задачи для |
||||
с постоянными коэффициентам |
|
|
||
уравнения (89).
129

Доказывается это утверждение просто. Подставим (90) в |
|||||
ные функции |
|
не зависят от времени, так |
|
|
|
нию время неΨ ( ) |
|
|
|
и собствен- |
|
уравнение (89). Учтём, что собственные значения |
|
||||
|
|
|
как по построе- |
||
|
входит в уравнение (87). В случае бесконечного |
||||
ряда потребуем его равномерную сходимость и равномерную сходимость рядов из производных по каждой пространственной переменной. Равномерная сходимость ряда позволяет менять порядок суммирования и дифференцирования. Имеем
|
|
|
|
+ |
2 0 ∆ ( ,2 ) − ( ) ( , ) = |
|
|||||
Ψ ( ) − / |
+ |
∆ Ψ ( ) − / − |
|||||||||
|
|
|
|
|
|
|
|
2 0 |
|
|
|
|
|
|
|
( ) Ψ ( ) − / = |
|
||||||
|
|
|
|
|
|
|
|
|
2 ∆Ψ ( ) − ( )Ψ ( ) |
= 0. |
|
− / Ψ ( ) + |
|||||||||||
Полученное уравнение |
2 0 |
|
|
||||||||
− |
|
|
|
+ |
|
|
0 ∆( , ) − ( ) ( , ) = 0 |
(91) |
|||
|
|
|
|
|
|||||||
совпадает с |
нестационарным уравнением Шрёдингера. |
|
|||||||||
|
|
|
2 |
|
|
|
|
||||
Метод построения решения (90) уравнения (91) аналогичен методу разделения переменных. Роль вспомогательной задачи
здесь играет задача на собственные значения для уравнения (87). |
||||||
не может установить в |
|
( , ) |
|
|
|
|
В КМ уравнение (91) принимается как постулат для нахож- |
||||||
дения волновой функции |
|
|
, физический смысл которой КМ |
|||
|
своей методологии. |
|
||||
строения уравнения (91), |
130 |
( , ) |
|
|||
В эфирной интерпретации, в соответствии со способом по- |
||||||
|
|
|
функция |
|
представляет собой |
|
волну малых возмущений скорости эфира, создаваемую в неко- |
||||
нечной или |
|
|
|
, движущейся |
торой своей малой окрестности частицей массы |
|
|||
со скоростью . В частном случае эта волна |
представляется ко- |
|||
|
0 |
|
||
бесконечной линейной комбинацией (90) монохроматических волн, не обязательно плоских.
Приведённые выше рассуждения можно проделать в обратную сторону. Исходим из уравнения (91). Подставляем в него раз-
ложение (90). Для каждой линейно независимой функции в (90) |
|
водит к двум дБ |
|
получаем уравнение (89). С помощью (88) приходим к уравнению |
|
(87). Замена |
на даёт уравнение (85). Подстановка (82) при- |
компонентам уравнения колебаний скорости (78). Прямые и обратные рассуждения показывают, что в случае
существования разложения (90) по собственным функциям урав-
нения (87), представляющих собой волны де Бройля, то есть |
||||||||
компоненты |
|
= / |
||||||
функции вида (82) с |
|
|
) |
|
, уравнение Шрёдингера (91) и две |
|||
этом |
= ,дБ = /( 0 |
|
|
|||||
|
|
|
уравнения малых колебаний скорости эфира (78) |
|||||
ется решением двух |
|
( , ) |
|
|||||
при |
2 |
2 |
|
|
|
|
2 эквивалентны. Иными словами, в |
|
|
случае решение |
|
|
|
уравнения Шрёдингера (91) явля- |
|||
|
|
|
|
компонент уравнения малых колебаний ско- |
||||
рости эфира (78) и наоборот. |
|
|||||||
4.2.3.Условия применимости уравнения Шрёдингера. Несостоятельность корпускулярно-волнового дуализма и туннельного эффекта частиц
Ещё раз подчеркнём, что основанием для анализа КМ с позиций теории эфира является значительно бо́льшая общность модели природы как движения эфира по сравнению с моделями КМ и теории относительности: в данной книге из исходных уравнений эфира математически выведены все основные законы физики, считавшиеся ранее экспериментальными фактами, а теория относительности и КМ не воспроизводят такой результат.
131
В п. 4.2.2 стационарное и нестационарное уравнения Шрёдингера получены из уравнения малых колебаний скорости эфира по методике, применяемой в КМ для объяснения причины выбора уравнения Шрёдингера среди других уравнений. Это
позволило установить следующее: |
|
|
||||
1. |
щений скорости |
|
(t, ) |
|
|
|
уравнение Шрёдингера не описывает саму частицу; |
||||||
2. |
волновая функция |
|
является волной малых возму- |
|||
|
скоростью ; |
эфира, создаваемой в некоторой своей |
||||
|
|
|
|
0 |
, движущейся со |
|
|
малой окрестности частицей массы |
|
||||
3.уравнение Шрёдингера применимо только в области, где скорость распространения,дБ = /( 0волны) в эфире может считаться равной ;
4. уравнение Шрёдингера описывает только двумерные явления и только в некоторой окрестности источника волны, а
не во всей вселенной; |
|
|
|
5. покоящаяся частица |
исключается из рассмотрения |
||
деления на ноль в формуле для |
|
. |
|
из-за возникновения = 0 |
|
|
|
В соответствии с выводом уравнения колебаний возмуще- |
|||
|
|
,дБ |
|
ний скорости эфира, потенциальная энергия , входящая в уравнение Шрёдингера, не должна зависеть от времени. Иначе это уравнение не будет следовать из модели, имеющей физическую интерпретацию. Основание для выхода за рамки обоснованной модели должно разъясняться, так как процедура такого выхода не единственна.
При выводе уравнения колебаний малых возмущений скорости эфира (78) отброшены вихревые течения, см. с 108. Уравнение Шрёдингера является следствием этого уравнения, поэтому тоже не описывает вихревые течения, связанные с объектом.
Из эфирной интерпретации уравнения Шрёдингера и волновой функции следуют фундаментальные выводы.
Математические результаты КМ сохраняются, но их интерпретация в корне меняется.
132
Согласно пп. 1–3, с точки зрения теории эфира КМ ошибочно отождествляет частицу с волной, которую создаёт эта ча-
стица, и ошибочно заполняет частицей всю вселенную. Необхо-
димо разделять свойства частицы и свойства среды, в которой она движется.
Так как КМ изучает малые возмущения скорости, создаваемые объектом в эфире, а не сам объект (пп. 2), то не в состоянии полноценно раскрыть устройство объекта. Поэтому эфирная интерпретация модели КМ показывает ошибочность приписывания объектупротиворечащихдругдругу свойств и частицы, и волны.
Объяснение КМ некоторых экспериментов туннельным эф-
фектом (просачиванием частиц сквозь потенциальный барьер) несостоятельно, так как: КМ описывает не саму частицу, а создаваемую ей волну (пп. 1); эта волна может двигаться со скоростью, отличной от скорости частицы, см., например, формулу Даламбера [62, с. 56], и занимать область, значительно бо́льшую, чем частица; вероятностная интерпретация волновой функции не обоснована (см. пп. 5 в п. 4.2.1) и поэтому не должна применяться для описания реальных явлений, тем более что КМ не описывает частицу.
Несостоятельность туннельного эффекта в КМ (просачивания частиц сквозь потенциальный барьер) рушит теорию электронной проводимости металлов и поверхностей электродов, а также туннельную теорию некоторых ядерных реакций.
В эфирном понимании, как и в классической физике, частица может находится только в области, разрешённой законом сохранения энергии. За границу этой области может выходить не сама частица, а порождаемая ею волна в эфире (течение эфира в общем случае). Таким образом, если какая-то теория может объяснить некоторое явление только понятием туннелирования из КМ, то необходимо либо пересмотреть такую теорию с учётом наличия эфира, либо отказаться от неё.
С точки зрения теории эфира КМ представляет собой своеобразную попытку изучения частицы по создаваемой её движением волне в эфире. Такой подход имеет основание. Например,
133
