
- •Предисловие к первому и второму изданиям
- •Предисловие к третьему изданию
- •Правовые вопросы
- •1. Иерархия математических моделей эфира как сплошной среды
- •1.1. Микроуровневая и макроуровневая модели эфира
- •1.2. Сравнение уравнений эфира с классическими уравнениями механики сплошной среды
- •1.3. Инвариантность уравнений неразрывности и движения эфира относительно преобразования Галилея
- •1.4. Плотность энергии, плотность мощности эфира. Давление эфира. Уравнение состояния эфира
- •2. Вывод уравнений Максвелла из уравнений эфира
- •2.1. Вывод обобщённых уравнений Максвелла – Лоренца из уравнений эфира
- •2.2. Вычисление электрического и магнитного полей
- •2.3. Векторный потенциал. Физическая интерпретация
- •2.4. Обобщённые уравнения колебаний электрического и магнитного полей
- •2.5. *Изучение вопроса об инвариантности обобщённых и классических уравнений Максвелла при преобразовании Галилея
- •2.5.2. Преобразование производных и операторов при замене переменных Галилея. Инвариантность уравнений неразрывности и движения эфира в эйлеровых переменных
- •2.5.3. Причина потери галилеевой инвариантности в обобщённых уравнениях Максвелла – неинвариантное преобразование исходных уравнений эфира. Инвариантность обобщённых уравнений Максвелла при досветовой скорости движения системы координат
- •2.5.4. Галилеева неинвариантность классических уравнений Максвелла в отсутствие среды и их инвариантность в эфирной трактовке при досветовой скорости движения системы координат
- •2.6. Общие замечания
- •3. Заряд, его электрическое поле. Теорема Гаусса. Закон Кулона. Электрический потенциал. Связь потенциального электрического поля с градиентом давления эфира. Сохранение заряда
- •4. Волновые процессы в эфире
- •4.1. Уравнения малых колебаний эфира. Некоторые волновые решения исходных уравнений эфира
- •4.2. Непригодность квантовой механики для полноценного описания природы
- •4.2.1. Анализ основ квантовой механики с позиций методологии математического моделирования
- •4.2.2. Вывод уравнения Шрёдингера из уравнений эфира. Эфирная интерпретация волновой функции. Ошибочность отождествления частицы и волны
- •4.2.4. Неадекватность интерпретации экспериментов, якобы обосновывающих квантовую механику
- •4.2.5. Основные выводы
- •5. Энергия электромагнитного поля
- •5.1. Общие формулы для плотностей энергии и мощности электромагнитного поля
- •5.2. Плотность энергии электромагнитной волны
- •5.3. Интерпретация энергии кванта света, постоянной Планка, волны де Бройля
- •6. Разрывы в эфире. Эффекты квантования
- •6.1. Самопроизвольное формирование разрывов
- •6.2. Условия на поверхности разрыва
- •6.3. Пример квантования
- •6.4. Эфирное представление условий разрыва магнитного и электрического полей
- •7. Вывод закона Био – Савара из уравнений эфира
- •9. Основной закон электромагнитной индукции. Электродвижущая сила. Правило Ленца
- •9.1. Основной закон электромагнитной индукции
- •9.2. Галилеева инвариантность основного закона электромагнитной индукции
- •10. Вихревое движение
- •10.1. Замкнутая вихревая трубка как основная устойчивая структура вихревого движения эфира
- •10.2. Вихревой импульс эфира. Закон сохранения вихревого импульса. Сохранения момента магнитного поля
- •11. Внешняя сила, действующая со стороны среды на завихренное течение эфира. Обобщение силы Жуковского для случая трёхмерного частично или полностью проницаемого объекта
- •11.1. Обобщение силы Жуковского
- •11.2. Движение элементарного объёма эфира в сильных внешних магнитном и электрическом полях. Ларморовский радиус вращения элементарного объёма эфира. Циклотронный эфирный резонанс
- •12. Электрический ток в проводниках
- •12.1. Токи вне и внутри проводников. Законы Ампера
- •12.2. Закон Ома. Электрическая проводимость
- •12.3. Закон Джоуля и Ленца
- •12.4. Влияние распределения скорости эфира внутри провода на создаваемое в нём магнитное поле и плотность электрического тока
- •12.5. Сверхпроводимость
- •13. Силовое воздействие эфира на объект, вызванное наличием градиента давления
- •14. Эфирный аналог теоремы Бернулли. Эффекты, обусловленные уравнением состояния эфира
- •14.1. Теорема Бернулли в эфире. Сравнение интеграла Бернулли с уравнением состояния эфира
- •14.3. Механизм воздействия обобщённой силы Жуковского
- •14.4. Принцип перемещения в эфире без отбрасывания количества движения
- •14.5. Плотность кинетической энергии эфира в электроне и протоне. Технологии, основанные на превращении осязаемой материи в поток эфира. Эфиробарический боеприпас
- •15. Классификация установившихся потоков эфира
- •15.1. Электрический поток эфира
- •15.2. Гравитационный поток эфира
- •15.3. Магнитный поток эфира
- •16. Силовое воздействие потока эфира на объект
- •16.1. Воздействие на заряженный объект. Сила Лоренца
- •16.2. Сила эфирного гравитационного притяжения. Гравитационная и инертная массы
- •17. Взаимодействие объектов
- •17.1. Закон Кулона для двух заряженных объектов
- •17.2. Закон гравитационного тяготения
- •18. Эфирная трактовка в электротехнике и электрохимии
- •18.1. Создание электрического тока в проводе. Падение напряжения на участке цепи
- •18.2. Мощность электрической цепи
- •18.3. Электрическое сопротивление в электрохимической ячейке и газовом разряде
- •18.4. Электрическое сопротивление в проводе
- •18.5. Электроёмкость, конденсаторы
- •18.6. Уравнение тока в контуре постоянной формы
- •18.8. Магнитная энергия замкнутого проводника с током в магнитном поле. Плотность магнитной энергии в цепи
- •18.9. Полная электромагнитная мощность цепи с током. Вектор Умова – Пойнтинга
- •18.10. Взрыв проволочек электрическим током в вакууме. Взрывная электронная эмиссия
- •18.11. Э.д.с. Жуковского. Униполярный генератор
- •18.12. Эффект Холла. Постоянная Холла
- •18.13. Электростатические эффекты
- •18.14. Электростатические устройства
- •18.15. Эксперимент для проверки закона сохранения заряда объектом на длительном промежутке времени
- •18.16. Удержание плазмы в тороидальных ловушках. Обобщение математических моделей плазмы
- •19. Интерпретация магнитных явлений
- •19.1. Потоки эфира, создаваемые доменом и постоянным магнитом
- •19.2. Магнит и ферромагнитный материал
- •19.3. Проводящий немагнитный материал и магнит
- •19.4. Проводник с током и магнит
- •19.5. Взаимодействие магнитов друг с другом
- •19.6. О попытках создания двигателя или генератора энергии на основе перемещения системы постоянных магнитов
- •20. Оценка плотности невозмущённого эфира
- •20.1. Единицы измерения плотности эфира
- •20.2. Оценки на основе экспериментов с лазерами
- •20.3. Оценки с использованием эфирной модели фотона и характеристик электромагнитного поля в нём
- •20.4. Оценка из эфирной модели фотона и его импульса
- •20.5. Оценки с применением эфирных моделей электрона и протона
- •20.6. Оценка на основе данных о кулоновском барьере
- •20.7. Основные выводы. Значение плотности эфира
- •20.8. Ошибочность принятия диэлектрической проницаемости вакуума в качестве невозмущённой плотности эфира
- •21. Структура носителей эфира – ньютониев. Кинетические эффекты в эфире и веществе
- •21.1. Давление невозмущённого эфира
- •21.2. Масса и размер носителей эфира – ньютониев. Среднее расстояние между ними
- •21.3. Распределение ньютониев при хаотическом тепловом и направленном движении
- •21.4. Краткий обзор моделей неравновесных, необратимых процессов и коэффициентов переноса в физике. Применение к описанию кинетики ньютониев
- •21.5. Теплопередача в эфире. Теплоёмкость эфира
- •21.6. Теплопередача в твёрдом веществе
- •21.7. Вязкость эфира
- •21.8. Самодиффузия в эфире
- •21.9. Электрическая проводимость эфира и вещества при отсутствии свободных зарядов
- •21.10. Оценка параметров эфирной модели электропроводности по опытным данным
- •21.11. Закон Видемана и Франца в металле и эфире
- •21.12. Давление эфира внутри твёрдых материалов и жидкостей
- •21.13. Слипание пластин с гладкой поверхностью, эффект Казимира. Фазовый переход состояний объектов. Радиоактивный распад
- •21.14. Явления в контактах
- •21.15. Электроотрицательность химических элементов
- •21.16. Плотность тока эфира в газовом разряде
- •21.17. Нецелесообразность применения понятия термодинамической энтропии в модели эфира
- •22. Оценка радиусов пограничных слоёв, обуславливающих возникновение силы Лоренца и силы гравитации
- •22.1. Заряженные объекты
- •22.2. Объекты, обладающие массой. Оценка скорости вращения гравитационного потока эфира вокруг Земли, его градиента давления и давления
- •23. Сводка экспериментальных фактов, подтверждающих наличие эфира
- •23.1. Основные общие законы электродинамики и гравитации
- •23.2. Электрический ток в проводе
- •23.2.1. Внутренняя противоречивость модели свободных электронов в твёрдом проводнике
- •23.2.2. Проблемы интерпретации опытов в электронной теории проводимости
- •23.2.3. Расчёт течения эфира внутри провода
- •23.3. Эксперименты с униполярным генератором. Эффект Аспдена
- •23.5. Теплопроводность металлов
- •23.5.1. Теплопроводность в поле силы тяготения
- •23.5.2. Теплопроводность во вращающемся диске
- •23.5.3. Теплопроводность при наличии вибрации
- •23.6. Вращение тел при отсутствии внешнего магнитного поля
- •23.6.1. Опыт Толмена и Стюарта с вращающейся катушкой
- •23.6.2. Инерционный опыт Лепёшкина с вращающейся спиралью
- •23.6.3. Создание магнитного поля вращающимся сверхпроводником, ферромагнетиком и другими объектами. Момент Лондона. Эффект Барнетта. Гравитомагнитный момент Лондона
- •23.6.4. Создание в эфире фантома вращением магнитного диска
- •23.6.5. Электромагнитное поле, создаваемое камертоном
- •23.6.6. Магнитное поле вращающегося немагнитного диска. Проект экспериментов
- •23.6.7. Опыт с вращающимся диском и флюгером
- •23.6.8. Ошибочные трактовки движения объектов в некоторых опытах как результата механического взаимодействия с эфиром
- •23.7. О разрушении материала вращением
- •23.8. Разрушение материала лазером
- •23.9. Эксперименты в техническом вакууме
- •23.9.1. Темновой ток
- •23.9.2. Темновой ток в присутствии магнита
- •23.9.3. Мельничка
- •23.9.4. Коловрат
- •23.9.6. Автоэлектронная эмиссия и фотоэмиссия электронов из проводника
- •23.9.7. Пробойный ток
- •23.10. Противодействие гравитации. Экранировка гравитационного потока эфира и его изменение
- •23.10.1. Вращение частично сверхпроводящего керамического диска в магнитном поле. Противодействие гравитации в эксперименте Подклетнова
- •23.10.2. Уменьшение веса электрона в вакуумной трубке, окружённой сверхпроводником, за счёт экранировки гравитационного потока эфира
- •23.10.3. Эксперименты В.В. Чернова по изменению силы тяжести. Создание фантомов в эфире вращающимся стальным маховиком, электрическим током и крутящимся магнитом
- •23.10.4. Экранировка гравитационного потока эфира атомарным порошком
- •23.10.5. Проект стенда для опытов с гравитацией
- •23.11. Черенковское излучение в эфире
- •23.12. Аномалии орбит первых спутников Фон Брауна
- •23.13. Эфирная интерпретация принципа работы электродвигателя на подшипниках
- •23.13.1. Простейшая эфирная модель электродвигателя на подшипниках
- •23.13.2. Анализ эфирной модели
- •23.13.3. Выводы и перспективы применения
- •23.14. Странное излучение, наблюдаемое при низкотемпературных ядерных реакциях (LENR)
- •24. Эфирная модель шаровой молнии
- •24.1. Аномальные свойства ШМ
- •24.2. Попытки объяснения ШМ без учёта эфира
- •24.3. Простейшая эфирная модель ШМ. Трактовка аномальных свойств
- •24.4. Интерпретация экспериментов Теслы с ШМ. Резонансный механизм аномальных явлений в электротехнических устройствах
- •25. Эфирная модель строения Земли
- •26. Информационная составляющая биологических систем и её проявления
- •27. «Путешествия» во времени
- •Заключение
- •Приложение 1. Вывод уравнения Ампера
- •Приложение 2. О поисках эфирного ветра
- •Приложение 3. О движущихся источниках света
- •Приложение 4. Траектории лагранжевых частиц для уравнения движения с нулевой правой частью
- •Приложение 5. Новые системы единиц измерения, связанные с эфиром
- •Приложение 6. Концентрации электронов и ионов в воздухе при низком давлении
- •Приложение 7. Ионный ветер в коронном разряде
- •Литература
- •Литература, добавленная во 2-м издании
- •Литература, добавленная в 3-м издании
- •Представления некоторых великих учёных об устройстве материи
- •Цитаты из высказываний об изданиях книги
- •Фальсификации, искажения, непонимание методологии и результатов книги

|
, полученной для фотонов, на частицы имеет ясное |
|
|
= |
|
|
Гипотеза (концепция) де Бройля о переносе формулы |
|
|
||
энергией . |
|
эфирное |
|||
,0 | | |
|
||||
обоснование как представление частицы с помощью периодиче- |
|||||
ского процесса в эфире, обладающего импульсом |
|
|
|
и |
|
6. Разрывы в эфире. Эффекты квантования
Различные подходы к построению математических моделей процессов с разрывными характеристиками движения подробно изложены, например, в [14, гл. VII, п. 4]. Здесь мы воспользуемся методом получения условий на поверхности разрыва, исходя из интегральных соотношений, в которых непрерывность искомых функций не подразумевается. Поверхности разрыва можно вводить как заданные поверхности с заданными законами их движения или как искомые поверхности, когда их форма и движение должны быть найдены при решении задачи.
6.1. Самопроизвольное формирование разрывов
Важно подчеркнуть, что в рассматриваемой математической модели эфира (4)–(6), даже на микроуровне (1)–(3), разрывы могут формироваться самопроизвольно. Например, в бездивергентном поле скоростей, а таким свойством обладают поле скоростей электромагнитной волны и поле скоростей фотона (см. [46] или
п. 4, 20.3), уравнение для скорости (30) при |
= 0 |
, |
= 0 |
, |
= 0 |
||
имеет вид |
, ( ) |
= 0. |
|
|
|||
|
|
|
|
|
|
|
|
Это трёхмерное уравнение Бюргерса – Хопфа. В одномерном случае уравнение Бюргерса – Хопфа хорошо изучено. В
147
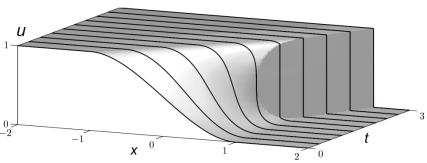
частности, показано, что на пересечении характеристик у его решения может формироваться резкий разрыв, например, в виде появления ударной волны (рис. 1), которая затем распространяется обычным для неё образом (см. п. 51 в [64]).
Отметим, что формирование такого разрыва позволяет надеяться на возможность создания вещества специальной системой приёмников высокочастотного электромагнитного излучения. Не исключено, что похожий процесс реализуется при фотосинтезе.
Рис. 1. Пример формирования ударной волны при решении одномерного уравнения Бюргерса – Хопфа.
6.2. Условия на поверхности разрыва
Уравнения в дифференциальной форме на поверхности разрыва не выполняются, так как в её точках не существует производных. В классической механике сплошной среды вблизи по-
верхности разрыва рассматриваются уравнения в интегральной |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
форме в некотором специальном выбранном неподвижном объ- |
||||||||||||||||||||
объёма в |
|
|
|
( ) |
|
|
|
|
|
|
|
|
+ |
|
с |
|||||
ёме |
|
с поверхностью |
|
и подвижном жидком объёме |
|
|
|
|
||||||||||||
ком |
|
|
|
|
|
, возникающем в момент времени |
|
|
|
|
из |
|||||||||
поверхностью |
|
|
|
|
|
|
||||||||||||||
|
|
|
результате движения среды [14, с. 393–395] (о жид- |
|||||||||||||||||
|
объёме см. также [21, с. 147]). Затем |
|
и |
|
|
стягиваются |
||||||||||||||
к точке на поверхности разрыва для |
получения |
условий в этой |
||||||||||||||||||
|
|
|
|
( ) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
148 |
|
|
|
|
|
|
|
|
|
|
|
|
точке. Стягивание к точке означает, что объём |
|
|
( ) |
берётся |
|||||||
сколь угодно малым (бесконечно малым). |
|
|
|
|
|
||||||
За бесконечно малое время |
частицы (носители) эфира в |
||||||||||
бесконечно малом объёме эфира |
|
|
перемещаются на малые |
||||||||
малый объём |
|
|
|
|
|
в процессе |
|||||
расстояния. Поэтому бесконечно |
|
( ) |
|
|
|
|
|
|
|
|
|
такой деформации можно рассматривать как |
состоящий из одних |
||||||||||
|
|
|
( ) |
|
|
||||||
и тех же частиц и имеющий границу, также состоящую из одних |
||||||
сматривать как жидкий объём. |
[ , + ] |
|
|
|
|
на |
и тех же частиц. То есть бесконечно малый объём эфира |
|
|
||||
бесконечно малом промежутке времени |
|
можно рас- |
||||
|
|
|
|
( ) |
|
|
Данное замечание обосновывает возможность использования методики [14, с. 393–399] для получения условий на поверхности разрыва, несмотря на то что значительные объёмы эфира на большом промежутке времени при неизотропной плотности не имеют интерпретации жидкого объёма (см. п. 1.2).
С учётом сделанного замечания, по аналогии с теорией механики сплошной среды [14, с. 393–399] из уравнений эфира в интегральной форме для плотности и скорости можно вывести условия, которые должны выполняться в эфире на поверхности разрыва функций в любой инерциальной или неинерциальной системе отсчёта
1 |
|
≡ |
1 |
lim |
1 |
|
2 |
|
|
2 |
(96) |
|
|
|
|
, |
|
|
|||||
1 |
1 1 |
∆ →0 0 |
∆ |
|
|
|
|
|
|
||
|
|
|
1 |
2 |
( − 2) ∙ , |
|
|||||
|
|
= −2 + 2 |
(97) |
||||||||
|
≡ |
|
lim |
1 |
|
|
. |
|
|
||
|
|
|
∆ →0 0 |
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
149 |
|
|
|
||
Здесь индексом обозначен предел с соответствующей стороны
поверхности разрыва, – давление (значение с обратным знаком |
||||||||||||||||||
по направлению |
|
= ( , ) |
|
|
|
|
|
|
|
тензора внутренних |
||||||||
диагонального |
элемента простейшего |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
напряжений, с. 38), |
|
– нормаль к поверхности разрыва |
||||||||||||||||
( , ) |
|
|
|
|
перехода со стороны 2 |
|
|
|
∆ |
|
||||||||
|
|
|
|
|
на сторону 1, |
пло- |
||||||||||||
|
– скорость перемещения поверхности разрыва, – = |
|||||||||||||||||
щадь элемента поверхности разрыва, |
|
– длина отрезка по нор- |
||||||||||||||||
мали к поверхности разрыва [14, с. |
393], |
|
|
и – внешние по- |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
верхностные плотности источника (в |
единице площади в еди- |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
= 0 |
= 0 |
|
|
|
||||
ницу времени) эфира и силы на поверхности разрыва. Если ис- |
||||||||||||||||||
точники , |
|
конечны в объёме |
|
, то |
|
|
|
|
, |
|
. |
|
|
|||||
Заданной системе дифференциальных уравнений можно сопоставить различные системы интегральных соотношений, которые для непрерывных движений эквивалентны между собой и с данной системой дифференциальных уравнений. Для движений с сильными разрывами различные системы таких интегральных соотношений могут быть неэквивалентными. Выбор интегральных законов, верных не только для непрерывных движений, но и в случае наличия внутренних в среде поверхностей сильных скачков, связан с дополнительными гипотезами, применимость которых должна апробироваться в опытах [14, с. 390]. Поэтому в эфире, наряду с соотношениями (96), (97), могут рассматриваться и альтернативные условия на разрыве.
Уравнение движения эфира отличается от уравнения движения классической механики сплошной среды (см. п. 1.2). Принципиальным отличием является присутствие дивергенции скорости в уравнении движения эфира (30). Для того чтобы непосредственно учесть это обстоятельство в условии на разрыве, сопоставим уравнению (30) некоторое интегральное уравнение и приведём его к форме, позволяющей применить на поверхности разрыва известный из классической механики сплошной среды результат.
В [21], с. 151, выведена общая формула
150

|
( ) ∙ = ( ) |
|
− ( ∙ ) + ( ∙ |
) ∙ , |
(98) |
||||
( ) |
перемещается ( ) |
|
|
|
= ( , ) |
|
|
||
где |
поверхность |
|
ограничивает подвижный объём, |
точки |
|||||
|
|
|
со скоростью |
|
. Лаконичное дока- |
||||
зательство этой формулы приведено в [21] на с. 152 с использо- |
||||||||||||||||||||||||||||||
( ) |
= ( ) |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
, |
) |
|
|
|
|
( |
, |
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= − |
|
|
|||||||||||||
ванием производной от интеграла по жидкому контуру. |
|
|
|
|
|
|||||||||||||||||||||||||
|
Воспользуемся формулой (98) для |
|
|
|
|
|
, |
|
|
|
|
|
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
( ∙ ) |
− ( ∙ ) ∙ , |
(99) |
|
|
|||||||||||||||
( ) ∙ |
= ( ) |
|
|
|
|
|||||||||||||||||||||||||
к |
|
|
|
|
|
= ( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|||||
вать как |
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормаль |
||||||||||
где вектор |
|
|
|
|
– внешняя по отношению к |
|
|
|
||||||||||||||||||||||
|
поверхности |
|
. Данный выбор |
|
|
и можно интерпретиро |
- |
|||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
рассмотрение |
неподвижной относительно скоростного |
|||||||||||||||||||||||||
поля |
|
|
|
|
поверхности |
|
|
|
|
. Левая часть формулы (99) пред- |
||||||||||||||||||||
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ставляет собой производную по времени от потока вектора ско- |
||||||||||||||||||||||||||||||
рости |
через поверхность жидкого объёма. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
силу уравнения (30) из (99) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
∙ |
= |
( ) |
− + |
+ |
∙ |
. |
|
|
(100) |
||||||||||||||||
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
,0 |
|
|
|
|
|
|
|
|
|
|
||||||
Выражение (100) можно интерпретировать как интегральную форму уравнения (30), которая остаётся справедливой и в более общем случае, например для разрывных функций.
По теореме Остроградского – Гаусса имеем
( ) ∙ = ( ) ∙ .
Тогда
151

|
|
|
( ) |
∙ = |
|
( ) |
− |
+ |
+ |
∙ . |
(101) |
|
|
|
|
|
|
|
,0 |
|
|||
Левая часть данной формулы совпадает с левой частью формулы (4.8) из [14, с. 395], если в (4.8) подынтегральную функцию
заменить на |
|
. |
|
|
|
|
||
Для правой∙ части |
по формуле (4.7 |
) из [14, с. 395], рассмат- |
||||||
риваемой для поверхности ( ), имеем′ |
||||||||
lim |
1 |
|
( ) |
− + + ∙ |
= 1 ∙ − 2 ∙ , |
|||
∆ →0 0 |
∆ |
|
|
,0 |
|
|||
где |
– источник скорости: |
|
||||||
|
|
|
|
≡ − + |
,0 |
. |
|
|
Взяв предел от равенства (101), получаем по аналогии с выводом формулы (4.20) из [14, с. 399], что в любой инерциальной или неинерциальной системе отсчёта на поверхности разрыва выполнено соотношение
1 |
1 |
|
1 |
( − 2) ∙ . |
(102) |
|
= 2 |
∙ |
+ ( ∙ )2 |
|
Условие (102) содержит одно уравнение, в то время как условие (97) является векторным и имеет три компоненты. В этом смысле использование (102) накладывает меньшие ограничения на искомые функции, чем использование (97).
Оба условия содержат не только нормальную компоненту скорости, но и другие её компоненты. Поэтому все компоненты
152
