Глава 8. Введение в математическую статистику

§1. Выборочный метод

Основной целью математической статистики является разработка методов получения научно обоснованных выводов о массовых случайных явлениях и процессах на основе статистических данных. Эта цель распадается на две задачи: 1-я задача  разработка способов сбора и группировки статистических данных; 2-я задача - разработка методов анализа статистических данных. Статистическими данными называются сведения о числе объектов в какой-либо обширной совокупности, обладающих теми или иными признаками. Всё множество изучаемых объектов называется генеральной совокупностью (Г.С.), число объектов в ней называется объемом и обозначается буквой N. Сплошное наблюдение часто оказывается невозможным и потому исследуется некоторая часть Г.С. Множество отобранных объектов называется выборочной совокупностью или выборкой, число объектов в выборке называется ее объемом и обозначается буквой n. При этом, если отобранный элемент после изучения возвращается в Г.С. и при отборе следующих элементов может быть выбран повторно, то выборка называется повторной; если же отобранный элемент не возвращается в Г.С., то выборка называется бесповторная.

Выборка называется репрезентативной, если она правильно представляет Г.С., т.е. процентное соотношение элементов, обладающих каким-нибудь свойством, одинаковое в Г.С. и в выборке. Выборка будет репрезентативной, если отбор ее элементов осуществляется случайно, причем каждый объект Г.С. имеет одинаковую возможность попасть в выборку. Для этого используют следующие виды отбора элементов выборки. Простой случайный отбор: все элементы Г.С. нумеруют и случайным образом выбирают номера. Типический отбор: вся Г.С. подходящим образом разбивается на несколько частей, и из каждой части случайным образом выбирается по одному элементу. Серийный отбор: вся Г.С. подходящим образом разбивается на несколько частей, случайным образом выбирается одна часть и все элементы этой части включаются в выборку. Механический отбор: все элементы Г.С. нумеруют, подбирают подходящее число m и выбирают по порядку каждый m-й ее элемент.

Пусть Х  некоторый признак или свойство изучаемых объектов. Тогда Х можно считать случайной величиной, ее значения для элементов выборки объема n обозначаются малыми буквами х₁, х₂, ..., х_n, и называются вариантами. Если вариант х_i встречается в выборке m_i раз, то m_i называется частотой, а отношение m_i : n называется относительной частотой или частостью этого варианта. Сумма частот всех различных вариантов равна объему выборки: m₁ + m₂ + ... + m_k = n. Таблица всевозможных вариантов х_i, расположенных в возрастающем ( или убывающем) порядке с указанием частот m_i или относительных частот w_i называется дискретным вариационным рядом частот или относительных частот данной выборки:

хi	х1	х2	. . .	хk
mi	m1	m2	. . .	mk

Эмпирической функцией распределения называется функция F*(х), которая каждому числу х ставит в соответствие относительную частоту n_x/n cобытия Х < х : F*(х) = n_x/n, где n_x - число вариант, меньших х; n - объем выборки. Эта функция служит аналогом теоретической функции распределения F(х) величины Х. Для наглядного изображения вариационного ряда строят полигон, являющийся аналогом теоретической функции плотности. Полигон частот - это ломаная линия, соединяющая точки

А₁(х₁; m₁), А₂(х₂; m₂), ... , А_k(х_k; m_k); полигон относительных частот - это ломаная линия, соединяющая точки А₁(х₁; w₁), А₂(х₂; w₂), ..., А_k(х_k; w_k), в прямоугольной системе координат.

Если Х является непрерывной случайной величиной, принимающей все значения из промежутка (а; b), то используют интервальные вариационные ряды. В качестве концов промежутка (а; b) берут наименьший (а х_min ) и наибольший (b х_max ) варианты, разбивают (а; b) на интервалы (a₁; b₁), (a₂; b₂), ... , (a_k; b_k) такие, что a₁ = а, b_k = b и для остальных концов выполняется

b_i = a_i+1. Число интервалов k зависит от объема выборки n и обычно определяется по формуле Стерджесса: k  (1+3,322lgn). Длины интервалов одинаковые h_i = (b а)/k. Затем находят частоты интервалов m_i - это число вариантов, входящих в i-й интервал. Интервальный вариационный ряд частот имеет вид

интервалы	(a1;b1)	(a2; b2)	. . .	(ak; bk)
частоты	m1	m2	. . .	mk

Для наглядного изображения интервального вариационного ряда строят гистограммы. Гистограмма частот - это плоская фигура в прямоугольной системе координат, составленная из прямоугольников, основаниями которых служат интервалы (a_i; b_i), а высоты Н_i вычисляются по формулам Н_i = m_i/h_i, где h_i -длина i-го интервала. Характерная особенность гистограммы в том, что площади прямоугольников равны частотам соответствующих интервалов.

Пусть изучается некоторый признак Х, и х₁, х₂, ... , х_n - варианты его значений для произвольной выборки объема n. Статистической оценкой признака Х называется функция (х₁, х₂, ... , х_n) от вариантов х₁, х₂, ... , х_n, с помощью которой вычисляется приближенное значение исследуемого признака: Х (х₁, х₂, ... , х_n). Выборка осуществляется случайным образом, поэтому оценку (х₁, х₂, ... , х_n) можно считать случайной величиной, тогда (х₁, х₂, ... , х_n) может иметь математическое ожидание М() и дисперсию D(). Наилучшими считаются оценки следующих трех видов. Оценка (х₁, х₂, ... , х_n) называется несмещенной, если ее математическое ожидание равно истинному значению изучаемого признака: М() = Х. Оценка (х₁, х₂, ... , х_n) называется эффективной, если ее дисперсия D() является наименьшей среди дисперсий всевозможных оценок данного признака. Оценка (х₁, х₂, ... , х_n) называется состоятельной, если ее значения стремятся к истинному значению признака при неограниченном возрастании объема выборки:

(х₁, х₂, ... , х_n)  Х при n

Пусть Х₁, Х₂, ..., Х_N - значения признака Х для элементов Г.С. и х₁, х₂,..., х_n - значения Х для элементов выборки. По ним определяются следующие величины:

1) 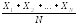=Х_Г - генеральная средняя;

2) 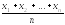=х_в - выборочная средняя;

3) 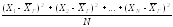=D_Г - генеральная дисперсия;

4) 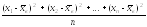=D_в - выборочная дисперсия;

5) _Г =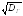-генеральное среднее квадратическое отклонение;

6) _в =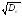-выборочное среднее квадратическое отклонение.

Если варианты х₁, х₂ , ... , х_n имеют частоты m₁ , m₂, ... , m_n , то указанные выше формулы принимают вид:

х_в = ,

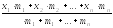D_в = .

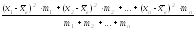Пусть некоторое событие А встречается М раз в Г.С. объема N, и  m раз в выборке объема n. Тогда величины 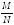=p и =w называются соответственно генеральная доля и выборочная доля события А.

Теорема 1. а). Выборочная средняя является несмещенной, эффективной и состоятельной оценкой для генеральной средней:

М(х_в) =Х_Г их_в Х_Г при n  .

б). Выборочная дисперсия является смещенной оценкой для генеральной дисперсии, и выполняется равенство

М(D_в) = .

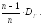в). Выборочная доля является несмещенной, эффективной и состоятельной оценкой генеральной доли:

М(w) = p и w  p при n  .

Доказательство (см. [4]).

При достаточно больших объемах выборки отклонение D_в от D_Г является незначительным, но при n < 20 это отклонение становится заметным, и для оценки D_Г рекомендуется находть исправленную дисперсию:S² =

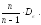
Легко доказывается, что S² и S являются несмещенными оценками D_Г и _Г, соответственно. Некоторые другие понятия и методы данной темы указаны в следующих примерах.

Пример 1. Из генеральной совокупности извлечена выборка объема

хi	2	5	7	10
mi	16	12	8	14

n = 50:

Требуется: 1) найти эмпирическую функцию распределения; 2) построить полигоны частот; 3) найти выборочную среднюю, выборочную и исправленную дисперсии.

Решение. 1). Для х  2 вариант, меньших х, нет, поэтому F*(х) = 0. Для 2< х 5 число вариант, меньших х, равно 16, поэтому F*(х) =16/50 = 0,32. Для 5< х  7 число вариант, меньших х, 16 + 12 = 28, поэтому F*(х) = 28/50 = 0,56. Для 7< х  10 число вариант, меньших х, равно16+12+8 = 36, поэтому F*(х) = 36/50 = 0,72. Для х > 10 все варианты меньше х, тогда F*(х) = 1. Получена следующая эмпирическая функция распределения:

0, если x 2,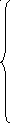

0,32, если 2 < x  5,

F*(x) = 0,56, если 5 < x  7,

0,72, если 7 < x  10,

1, если x > 10 .

2). Полигон частот - это ломаная А₁(2; 16), А₂(5; 12), А₃(7; 8), А₄(10;14); полигон относительных частот - это ломаная В₁(2; 0,32), В₂(5; 0,24), В₃(7; 0,16), В₄(10; 0,28).

Y Y

16 А₁ 0,4

А₄ В₁

12 А₂ 0,3 В₄

А₃ В₂

8 0,2 В X X

0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10

Рис.4

3). Выборочная средняя равна х_в = (216+512+78+1014)/50 = 5,76. Выборочная дисперсия равна D_в = [(2 5,76)²16 + (5  5,76)²12 + (75,76)²8 + (10 5,76)²14]/50 = 9,9424. Исправленная дисперсия равна S² = 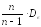=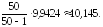Ответ:х_в = 5,76; D_в = 9,9424; S²  10,145.

Пример 2. Ниже приведены результаты измерения роста (X см) случайно отобранных 100 студентов.

X	154158	158162	162166	166170	170174	174178	178182
mi	10	14	26	28	12	8	2

1). Найти выборочную среднюю, выборочную и исправленную дисперсии.

2). Построить гистограмму частот.

Решение. 1). В качестве вариантов берут середины интервалов х_i: 156, 160, 164, 168, 172, 176, 180. Они отстоят друг от друга на одинаковых расстояниях, поэтому можно ввести условные варианты по формуле u_i = 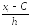, гдеС  так называемый ложный ноль, (в качестве С рекомендуется выбирать вариант с наибольшей частотой), h – шаг, (он равен расстоянию между вариантами). Значениями условных вариант являются небольшие целые числа и потому многие вычисления существенно упрощаются. Для условных вариантов находят среднее значениеu и средний квадратu², затем х_в и D_в находят по формулам: х_в =u h + С; D_в = (u²  (u )²)h². Здесь

С = 168, h = 4. Составляется расчетная таблица, которая заполняется по формулам, указанным в верхней строке.

хi	mi	ui	miui	miui2
156	10	-3	-30	90
160	14	-2	-28	56
164	26	-1	-26	26
168	28	0	0	0
172	12	1	12	12
176	8	2	16	32
180	2	3	6	18
å	100		-50	234

В нижней строке указаны суммы чисел по каждому столбцу, с их помощью вычисляются средние значения условных вариант:u= 50:100 = 0,5; u²=234:100 = 2,34. По указанным выше формулам находятся искомые величины: х_в = 0,54 + 168 = 166; D_в = (2,34 (0,5)²)4² = 33,44; S² = 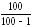33,44 33,778.

2). На оси ОХ откладываются интервалы и на них строятся прямоугольники, высоты которых вычисляются по формуле Н_i = 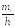:Н₁ = 2,5; Н₂ = 3,5; Н₃ = 6,5; Н₄ = 7; Н₅ = 3; Н₆ = 2; Н₇ = 0,5.

Y

7

1

X

0 154 158 162 166 170 174 178 182

Рис.5.

1. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. – М., «Наука»., 1980. -236 с.

2. Минорский В. П. Сборник задач по высшей математике. –М.: Изд-во «Наука»., 1971.-352 с.

2. Сахарников Н. А. Высшая математика. Изд-во Ленинград. ун-та, 1973,

-473 с.

3. Фаддеев Д.К., И.С.Соминский Сборник задач по высшей алгебре, -М., «Наука», 1977

4. Кремер Н. Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ,-2000.