
- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
Методы интегрирования дифференциальных уравнений
1-й
метод.
Метод
разделения
переменных.
Этот
метод применяется к уравнениям вида
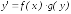 ,
т.
е. правая часть является произведением
двух функций от разных переменных
x
и y.
Такое уравнение записывается в виде
,
т.
е. правая часть является произведением
двух функций от разных переменных
x
и y.
Такое уравнение записывается в виде
 .
.
Выражения
dy
и dx
называются дифференциалами
переменных.
Известно, что зависимость между этими
величинами выражается равенством: dy
=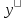 ∙dx
. Поэтому при умножении обеих частей
этого уравнения на дробь
∙dx
. Поэтому при умножении обеих частей
этого уравнения на дробь
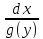 получится равносильное дифференциальное
уравнение (правда, при условии g(y)
0, но об этом позже):
получится равносильное дифференциальное
уравнение (правда, при условии g(y)
0, но об этом позже):
 ,
,
в котором переменные x и y находятся в разных частях. Такое уравнение называется дифференциальным уравнением с разделёнными переменными. К обеим частям этого равенства приписывают впереди символы интегралов, в результате получится так называемое равенство в квадратурах, которое теоретически считается решением рассматриваемого уравнения. А если эти интегралы будут вычислены, то получится общий интеграл этого уравнения
Замечание 1. При разделении переменных часто приходится делить обе части уравнения на некоторые выражения, содержащие неизвестную функцию. При этом надо обязательно предполагать, что делитель не равен 0. В результате некоторые значения переменной y становятся недопустимыми, и они могут не войти в полученное общее решение уравнения. В таких случаях надо отдельно рассматривать случаи, когда делитель равен 0. Часто полученные при этом значения y являются особыми решениями исходного уравнения, и их прибавляют к общему решению.
2-й метод. Метод интегрирования однородных дифференциальных уравнений 1-го порядка. Такое уравнение имеет вид
y = f(x,y),
где правая часть является однородной функцией, которая удовлетворяет следующему условию: для любого множителя t имеет место:
f(t∙x, t∙y) = f(x,y).
Если
в этом равенстве взять
t
=
 ,
то получится равенство:
f(1,
,
то получится равенство:
f(1,
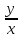 )
=
f(x,y)
.Тогда
замена u
=
)
=
f(x,y)
.Тогда
замена u
=
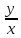 приводит это дифференциальное уравнение
к виду:
приводит это дифференциальное уравнение
к виду:
u
+x = f(1,u),
= f(1,u),
которое является с разделяющимися переменными. Находится решение этого уравнения и производится обратная замена y= x∙u.
3-й метод. Метод Бернулли. Он применяется к линейным уравнениям и к некоторым другим уравнениям.
Определение 4. Линейным дифференциальным уравнкнием 1-го порядка называется уравнение вида
 +
p∙y
=
q,
+
p∙y
=
q,
где p, q - некоторые функции от x. Согласно условиям существования решения задачи Коши, эти функции должны быть непрерывными.
Решение
разыскивается в виде произведения двух
неизвестных функций: производится
замена: y=u∙v
и
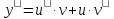 .
Получается
уравнение
.
Получается
уравнение
 +
p∙u∙v
= q.
+
p∙u∙v
= q.
Дальше
решение разделяется на две части. 1-я
часть.
В полученном уравнении второе и третье
слагаемые группируются вместе ( + p∙u∙v),
выносится общий множитель u
за скобку
+ p∙u∙v),
выносится общий множитель u
за скобку
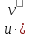 + p∙v)
и
полученное в скобке выражение
приравнивается к 0:
+ p∙v)
и
полученное в скобке выражение
приравнивается к 0:
 + p∙v
=
0. В результате исходное уравнение
упрощается:
+ p∙v
=
0. В результате исходное уравнение
упрощается: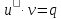 .
Но сначала, в качестве v
подбирается функция, являющаяся решением
предыдущего уравнения. Оно чвляется с
разделяющимися переменными, получается:
.
Но сначала, в качестве v
подбирается функция, являющаяся решением
предыдущего уравнения. Оно чвляется с
разделяющимися переменными, получается:
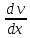 = -p∙v,
тогда
= -p∙v,
тогда
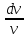 =
- pdx
и
=
- pdx
и
 =
-
pdx.
Отсюда
ln|v|
= -pdx
или v
=
=
-
pdx.
Отсюда
ln|v|
= -pdx
или v
=
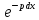 ,
(здесь константу «с»
не пишут).
,
(здесь константу «с»
не пишут).
2
-я часть. Найденную
функцию
v
подставляют назад во вторую часть
уравнения, получается
 .
Отсюдаu
=
.
Отсюдаu
= 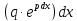 + c.
Функции u
и
+ c.
Функции u
и
 найдены, и искомое решение равноy
=
u∙v
=(
найдены, и искомое решение равноy
=
u∙v
=(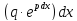 + c)(
+ c)( ).
).
4-й метод. Метод вариаций (или метод Лагранжа). Рассматривается линейное уравнение из предыдущего пункта. Ему соответствует уравнение вида
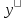 +
p∙y
=
0,
+
p∙y
=
0,
которое
называется линейным однородным
уравнением. Оно решается методом
разделения переменных так, как это было
описано в первой части предыдущего
пункта. В соответствующий момент
получается общий интеграл вида:
ln|y|
= -pdx+
ln|c|,
(параметр с не отбрасывается). Это
равенство преобразуется к виду y
= c∙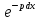 .
Далее, решение полного линейного
уравнения отыскивается в виде y
= c(x)∙
.
Далее, решение полного линейного
уравнения отыскивается в виде y
= c(x)∙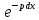 .
Понимая под с некоторую функцию от x.
Такое решение существует, действительно
если эту функцию подставить в исходное
уравнение, то получится:
.
Понимая под с некоторую функцию от x.
Такое решение существует, действительно
если эту функцию подставить в исходное
уравнение, то получится:
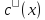 ∙
∙ +c(x)∙
+c(x)∙ + p∙
c(x)∙
+ p∙
c(x)∙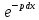 =q.
=q.
Здесь
 =
-p∙
=
-p∙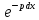 ,
поэтому получилось уравнение:
,
поэтому получилось уравнение:
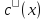 ∙
∙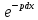 =
q.
=
q.
Отсюда
с(x)
=(q∙ )dx+
)dx+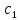 ,
и у
=(
,
и у
=( +
+
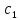 )(
)( ).
).
Пример
4. Найти
общее решение
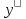 +y∙tgx
= 2xcosx.
+y∙tgx
= 2xcosx.
Решение.
Соответствующее линейное однородное
уравнение
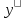 +y∙tgx
= 0 имеет решение y
=
c(x)∙cosx.
Функция c(x)
удовлетворяет уравнению
+y∙tgx
= 0 имеет решение y
=
c(x)∙cosx.
Функция c(x)
удовлетворяет уравнению
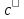 =2x.
Поэтому с(x)=
=2x.
Поэтому с(x)=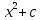 .
Общее решение равноy=
.
Общее решение равноy= .
.
5-й Метод. Он применяется к так называемым уравнениям Бернулли, имеющим иид:
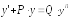 ,
,
где p, q – непрерывные функции от x.
Это
уравнение можно решать описанным выше
методом Бернулли, или следующим более
простым методом. Обе части уравнения
делятся на
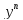 и делается замена:
и делается замена:
 , гдеz
– новая неизвестная функция. В результате
получается линейное уравнение относительно
функции z:
, гдеz
– новая неизвестная функция. В результате
получается линейное уравнение относительно
функции z:
 .
Указанным выше методом находится общее
решение этого уравнение, и делается
обратная замена:y
=
.
Указанным выше методом находится общее
решение этого уравнение, и делается
обратная замена:y
=
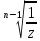 .
.
