§2. Задачи, приводящие к понятию производной функци

Залача о мгновенной скорости движения. Пусть точка М движется вдоль числовой оси ОХ и в каждый момент времени t ее координата равна s(t). Тогда равенство s = s(t) называется уравнением движения точки М. Пусть рассматривается момент t_o, и t - некоторый другой момент, (см. рис.2). В момент t_о точка М имеет координату s(t_о) и в момент t  координату s(t). Тогда разность s = s(t)  s(t_о) есть расстояние, пройденное точкой М за время

t = (t t_o), а отношение 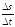=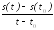естьсредняя скорость движения.

s

0 s(t₀) s(t) x

Рис.2.

Но более правильное представление о скорости движения в момент t₀ дает предел этого отношения, когда t стремится к t_o, и этот предел называется мгновенной скорстью движения точки М:

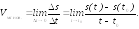
Ясно, что этот предел является производной функции s(t) в точке t_o. Получен следующий физический смысл производной: если функция s(t) задает уравнение движения точки, то производная s(t_o) есть мгновенная скорость движения точки в момент t_o.

Аналогично показывается, что производная второго порядка s(t_o) есть мгновенное ускорение движения точки в момент t_o,.

Пример 6. Пусть S = t³ – 6t² + t  расcтояние в метрах, пройденное телом в течение t секунд. Определить скорость и ускорение при t = 3 c.

Решение. Скорость v в момент t равна производной S= 3t²  12t + 1, тогда при t = 3 скорость равна v = 33²  123 + 1= м/с. Ускорение w в момент t есть производная от скорости: w = v = 6t  12. При t = 3 ускорение равно w = 63  12 = 6 м/с².

Задача о предельных издержках производства. Пусть х обозначает количество выпускаемой продукции и у  издержки производства. Тогда у считается функцией от количества выпускаемой продукции: у = f(x). Пусть в некоторые моменты времени выпуски продукции составили х_о и х (ед.), а издержки производства равны f(x_o) и f(x) (ден. ед.), соответственно. Тогда х = х  х_о есть прирост продукции, у = f(x)  f(x_o)  приращение издержек производства, и отношение 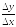=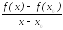называетсясредним приращением издержек производства на единицу продукции. Но для характеристики скорости изменения денежных затрат вводятся так называемые предельные издержки производства, которые определяются, как производная этой функции:

Аналогично с помощью производной могут быть определены предельная выручка, предельная себестоимость и другие предельные величины. При этом средние величины характеризуют состояние соответствующего экономического объекта, а предельные величины характеризуют скорость изменение этого объекта. Таким образом, производная выступает как скорость изменения некоторого экономического процесса. Однако, следует учесть, что экономика и другие социальные науки не всегда позволяют использовать предельные величины в силу неделимости многих экономических объектов и в силу прерывности экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). Вместе с тем в ряде случаев оказывается возможным отвлечься от дискретности этих показателей и эффективно использовать предельные величины.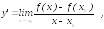

Задача о темпе производственной функции. Пусть функция у = f(t) описывает некоторый производственный показатель. Тогда рассматривается относительная скорость изменения этой функции, которая называется темпом данного показателя и определяется как логарифмическая производная:

Например, рассматривают темпы роста производительности труда, темпы изменения себестоимости продукции.

Задача об эластичности функции. Эластичностью функции у = f(x) называется предел отношения относительного приращения функции к относительному приращению аргумента х при х  0:

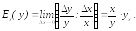
Коэффициент эластичности Е_х(y) показывает приближенно, на сколько процентов изменится функция y при изменении аргумента х на 1%. Например, если y – спрос на некоторый товар и х – цена товара, то Е_х(y) показывает: на сколько процентов изменится спрос при изменении цены на 1%. Если |Е_х(y)| > 1, то спрос считают эластичным, если |Е_х(y)| = 1, то – нейтральным, если |Е_х(y)| < 1, то спрос неэластичен.

Задача о касательной. Рассматривается график функции у = f(x) и точка М_о(х_о; у_о) на этом графике. Требуется найти уравнение касательной к графику в точке М_о.

Так как М_о лежит на графике, то ее координаты удовлетворяют уравнению графика, т.е. выполняется равенство: у_о = f(x_o).

y

y M

у = f(x) y

y₀ M₀ dy

0  x₀ х x

Рис.3. 

Пусть М(х; у) – произвольная точка на графике, тогда ее координаты удовлетворяют равенству: у = f(x). Пусть эти точки проецируются на оси координат (см. рис. 3), и M_оN параллельна оси ОХ. В треугольнике МNM_o: M_оN = (х х_о) =х, NM = (у  у_о) = у, отношение NM к M_оN равно тангенсу угла NM_оM, т.е. 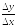=tg(NM_оM). Касательной к графику функции f(x) в точке М_о называется прямая линия, к которой стремятся хорды М_оМ, когда точка М стремится к точке М_о по графику. Если точка М будет двигаться по графику к точке М_о, то х будет приближаться к х_о, и отношение 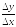будет стремиться кtg, где   угол наклона касательной к оси ОХ . Величина tg называется

угловым коэффициентом касательной. В то же время предел отношения 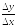прих  х_о равен производной функции f(x) в точке х_о. Получен следующий геометрический смысл: производная функции f(x) в точке х_о равна угловому коэффициенту касательной к графику этой функции в точке М_о.

Теперь, применяют уравнение (6) из главы 2 части 1, и получают следующее уравнение касательной к графику f(x) в точке М_о:

(3)

у = f (x_o)(х  x_o) + f(x_o)

Пример 7. Найти уравнения касательных к параболе у = 0,4х²  3,2х + 7,8 в точках пересечения ее с прямой у = 0,4х + 2,2.

Решение. Координаты точки пересечения линий удовлетворяют обоим уравнениям, тогда эти координаты являются решениями системы:

у = 0,4х + 2,2 и у = 0,4х² 3,2х + 7,8. Здесь два решения: х₁ = 7, у₁ = 5 и х₂ = 2, у₂ = 3. Следовательно, получены две точки пересечения А(7; 5) и В(2; 3). Абсциссу вершины параболы С находят из уравнения у(x) = 0, т.е. 0,8x  3,2 = 0, отсюда x = 4. Это подставляют в уравнение параболы: y = 1,4; тогда C(4; 1,4)  вершина параболы (см. рис.4). Далее, применяют уравнение (3). Для этого находят производную: у = 0,8х 3,2. Значения у в точках х₁ = 7 и х₂ = 2 являются угловыми коэффициентами касательных в точках А и В: k₁ = 0,873,2 = 2,4 и k₂ = 0,82 3,2 = 1,6. Эти значения подставляют в (3).

1) у = 2,4х 11,8  уравнение касательной в точке А. 2) у = 1,6х + 6,2  уравнение касательной в точке В.

y y = 0,4x²  3,2x + 7,8

y=0,4x+2,2 A

B

С y =2,4x11,8

y =1,6x+6,2

0 x

Рис.4.

Пусть функция y = f(x) имеет конечную производную в точке х₀ :

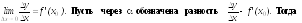
  0 при х  0; отсюда y = f (x₀)х + х . При этом первое слагаемое является линейной частью приращения 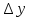относительно 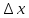,а второе слагаемое является бесконечно малой 2-го порядка.

Определение 3. Дифференциалом функции f(x) для x₀ и х, называется линейная часть f (x₀)х приращения 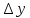; обозначения: dy, df.

В частности, дифференциал функции y = x равен х, т.е. dх = х. Поэтому вместо х пишут dх, тогда dy принимает вид:

(4)

dy = f (x₀)dх

На рис.3 дифференциал dy удачно выделен, как часть y, и говорят, что dy есть приращение касательной. Если f (x₀)0, то dy является главной частью приращения функции y. Поэтому можно считать, что при достаточно малом х приращение функции y приближенно равно ее дифференциалу: y  dy. Отсюда получается формула для приближенного вычисления значений функции:

f(x)  f(x₀) + f (x₀)dх

(5)

При этом считается, что погрешность такого равенства имеет порядок (.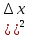

Пример 8. Для функции y = x³ – 2x +1, найти приращение y и дифференциал dy, соответствующие x₀ = 1 и х = 0,1.

Решение. Здесь x₀ = 1, х = 0,1, поэтому х = 1,1.

Тогда f(x) = f(1,1) = 1,1³ – 2^. 1,1 +1 = 0,131; f(x₀) = f(1) = 1³ – 2^. 1 +1 = 0, 1;

f (x)= 3x² – 2; f (x₀)= f (1)3^. 1² – 2 = 1. Получается: y = f(x) – f(x₀) = 0,131– 0 = 0,131; dy = f (x₀)dх = 10,1 = 0,1. Тогда погрешность равна 0,031, и это соответствует порядку (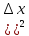 = 0,01.

Пример 9. Вычислить приближенно 34 помощью дифференциала.

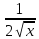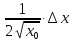Решение. Рассматривается функция y = x, и пусть x₀ = 36, х = 34. Тогда х = 34 – 36 =  2; f(x₀) = 36 = 6; f (x)= ; следовательно, dy = = ∙(-2)  -0,167. Теперь, применяется формула (5):34 

 - 0,167 5,833. Пусть истинное значение34 = 5,831 (найдено с помощью калькулятора). Тогда получена погрешность 0,002.