§4. Ранг матрицы и неопределенные системы

Пусть в числовой матрице А = (a_ij) – размера mn, выбраны какие-нибудь k строк (с номерами i₁,…, i_k), и k столбцов (с номерами j₁,…, j_k ).

Определение 10. Минором порядка k матрицы А называется определитель k-го порядка, образованный элементами, расположенными на пересечении выбранных строк и столбцов, обозначение:

.

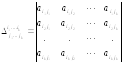Минор порядка k матрицы А называется базисным, если он отличен от нуля, а все миноры порядка k+1 равны нулю или не существуют. Очевидно, что базисные миноры имеют один и тот же порядок.

Определение 11. Рангом матрицы А называется порядок ее базисного минора, обозначение: rang(A).

Из предыдущих определений следует, что rang(A) есть наивысший пордок отличного от нуля минора матрицы А. Для нулевой матрицы ее ранг равен нулю. Матрицы А и В, имеющие одинаковый ранг, называются эквивалентными, обозначение: А  В.

Вычисление ранга матрицы осуществляют с помощью эквивалентных преобразований, описанных в методе Гаусса, и основаны на следующем утверждении.

Теорема 2. Транспонирование и эквивалентные преобразования не меняют ранг матрицы.

Доказательство осуществляется методом математической индукции по рангу, но в этом курсе оно не рассматривается (cм.[1. с. 166]).

На этой теореме основано следующее правило вычисления rang(A).

Исходная матрица с помощью эквивалентных преобразований приводят к описанному выше виду трапеции (9). При этом отбрасывают все нулевые строки. Тогда количество оставшихся строк полученной матрицы равно рангу исходной матрицы.

Пример 21. Найти ранг следующей матрицы:

А =

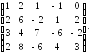
Решение. 1-й шаг. 1-я строку умножают на 2 и прибавляется ко 2-й и

4-й строкам, затем 1-я строка умножают на 3 и прибавляют к 3-й строке. В результате получают следующую эквивалентную матрицу:

А₁ = .

2-й шаг. 2-я строку прибавляют к 3-й строке, затем 2-я строку умножают на 2 и прибавляют к 4-й строке:

А₂ = .

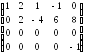3-й шаг. 3-ю строку отбрасывают, и переставляют местами 3-й и 5-й столбцы:

А₃ =

4-й шаг. Матрица А₃ имеет вид трапеции. В ней минор, расположенный в первых трех строках и столбцах отличен от нуля, его порядок равен 3, следовательно, rang(A₃) = 3, и, по теореме 2, rang(A) = 3.

Определение 12. Пусть C₁, C₂, …, C_k - строки некоторой матрицы А. Линейной комбинацией этих строк называется выражение m₁C₁ + m₂C₂ + …+ m_kC_k, где m₁, m₂, …, m_k - числовые коэффициенты. Аналогично определяется линейная комбинация столбцов. Строки (или столбцы) называются линейно зависимыми, если существует их линейная комбинация, в которой имеются коэффициенты отличные от нуля, и которая равна нулевой строке (столбцу). В противном случае строки или столбцы называются линейно независимыми.

Замечание 4. Введенные в данном параграфе понятия являются основными в рассматриваемом разделе линейной алгебры, и их определения надо знать наизусть. В более подробном изложении этого курса для них доказываются следующие утверждения [1, с.170-173].

Теорема о базисном миноре. В произвольной матрице каждая строка (или столбец) равна линейной комбинации строк (или столбцов), в которых расположен базисный минор матрицы.

Важным следствием этой теоремы является следующее утверждение.

Теорема об определителе. Определитель матрицы равен нулю тогда и только тогда, когда его строки (или столбцы) являются линейно зависимыми.

Пример 22. Ранее было показано, что следующий определитель равен нулю:

Тогда пусть С₁ = (1 2 3), С₂ = (4 5 6), С₃ = (7 8 9) строки этого определителя, легко видеть, что их линейная комбинация С₁ 2С₂ + С₃ (0 0 равна нулевой строке, т. е. эти строки определителя линейно зависимые.

Следующее утверждение дает вторую форму определения ранга матрицы.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу линейно независимых строк (или столбцов) в этой матрице.

Центральным утверждением в линейной алгебре является следующая важная теорема.

Теорема Кронекера-Капелли. Система (3) имеет хотя бы одно решение в том и только в том случае, когда ранг основной матрицы системы равен рангу расширенной матрицы этой системы.

Доказательство. Определения A и А* даны в (8). Пусть 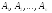обозначают 1-й, 2-й, … , n-й столбцы матрицы и В - столбец свободных членов (3). Тогда эту систему можно записать в виде: .

1. я часть (необходимость). Пусть система (3) совместна, тогда сущест-

вуют числовые значения неизвестных 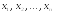, при которых выполняется предыдущее равенство. Это означает, что n+1-й столбец В в расширенной мат

рице А* является линейной комбинацией первых столбцов. Следовательно, прибавление столбца В к сталбцам матицы А не увеличивает число линейно независимых столбцов в матрице А*. Тогда по предыдущей теореме rang(A) = rang(A*).

2-я часть (достаточность). Пусть rang(A) = rang(A*). Тогда базисный минор матрицы А является базисным минором матрицы А*. Следовательно, столбец В равен линейной комбинации столбцов, в которых расположен базисный минор, и потому В есть линейная комбинация первых n столбцов матрицы А. Набор коэффициентов этой линейной комбинации, (включая 0), являются решением данной системы, т.е. система совместна. Теорема доказана.

Теперь рассматривают множество решений неопределенной системы линейных уравнений. Пусть система (3) приведена к равносильному виду трапеции (7), в ней нет противоречий и отброшены нулевые равенства. Более того, можно считать, что ее неизвестные занумерованы так, что система имеет вид

а₁₁^*х₁ + а₁₂^*х₂ + ... + а_1k^*х_k+ ... + а_1n^*х_n = b₁^*,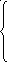

а₂₂^*х₂ + ... + а_2k^*х_k+ ... + а_2n^*х_n = b₂^*,

 ............................................... (10)

а_kk^*х_k + … + а_nn^*х_n = b_k^*,

где коэффициенты а₁₁^*, а₂₂^* , …, а_kk^* отличны от нуля и k – ранг матрицы коэффициентов исходной системы.

Эту систему можно преобразовать к равносильному виду:

х₁ = b₁^**  (а_1k+1^**х_k+1 + ... + а_1n^**х_n),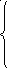

х₂ = b₂^**  (а_2k+1^**х_k+1 + … + а_2n^**х_n),

 …………………………………. (11) х_k = b_k^**  (а_kk+1^**х_k+1 + … + а_kn^**х_n),

где b_i^**, a_ij^**- уже другие числа, полученные в результате указанных выше преобразований.

Неизвестные справа х_k+1, х_k+2, …, х_n называются свободными, они могут принимать любые значения; неизвестные слева х₁, х₂, …, х_k называются зависимыми. Для каждого набора значений свободных неизвестных зависимые неизвестные получают определенные значения по формулам (11), и весь образовавшийся набор значений х₁, х₂, …, х_k, х_k+1, …, х_n является решением исходной системы. Такое описание множества решений системы (3) называется параметрическим, здесь свободные неизвестные являются параметрами.

Но существует другой более красивый метод описания таких решений, с помощью так называемых базисных решений.

Системе уравнений (3) соответствует система (12) с той же матрицей коэффициентов, но все свободные члены которой равны нулю: Такая система называется однородной, она всегда совместна, так как нулевой набор значений неизвестных является ее решением.

а₁₁х₁ + а₁₂х₂ + ... + а_1nх_n = 0,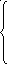

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_n = 0,

.............................................. (12)

а_m1х₁ + а_m2х₂ + ... + а_mnх_n = 0.

Для нее верны все предыдущие рассуждения, поэтому (12) равносильна системе (11) с b₁^** = 0, b₂^** = 0,…, b_n^** = 0. Оказывается, что множество всех решений системы (3) образует так называемое линейное пространство, которое подробно рассматривается в главе 4. В этом пространстве следующим образом строятся базисные решения.

Свободным неизвестным придаются n – k следующих наборов значений:

1) х_k+1 = 1, х_k+2 = 0, …, х_n = 0;

2) х_k+1 = 0, х_k+2 = 1, …, х_n = 0;

…………………………….

n – k) х_k+1 = 0, х_k+2 = 0, …, х_n = 1.

Для каждого такого набора вычисляются значения зависимых неизвестных по формулам (11) (с b₁^** = 0, b₂^** = 0,…, b_n^** = 0). В результате получится n – k решений системы (12), которые записывают в виде столбцов, обозначенных через С₁, С₂, …, С_n-k . Главные свойства решений (13) в том, что они являются линейно независимыми и любая линейная комбинация этих решений является решением системы (12). Также верно обратное утверждение о том, что любое решение системы (12) представимо в виде линейной комбинации этих решений.

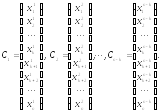(13)

Поэтому такие решения называются базисными решениями однородной системы (12), а их совокупность называется фундаментальной системой решений.

Далее, эти базисные решения используют для описания множества решений общей системы (3) согласно следующему утверждению.

Теорема (об общем решении). Если столбец чисел D₀ размера 1n есть некоторое решение системы (3) и C₁, C₂, … , C_nk  фундаментальная система решений соответствующей однородной системы (12), то для любых чисел m₁, m₂, …, m_nk линейная комбинация

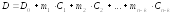(14)

является решением системы (3). И наоборот, каждое решение системы (3) представимо в виде (14).

Доказательство (см. [1. с. 180]).

Выражение, стоящее в правой части равенства (14) называется общим решением системы линейных уравнений (3).

Пример 23. Найти общее решение следующей системы уравнений в параметрическом виде и через базисные решения однородной системы:

х₁ – 2х₂ + 3х₃ – 4х₄ = 4,

х₂ – х₃ + х₄ = –3,

х₁ + 3х₂ – 3х₄ = 1,

–7х₂ + 3х₃ + х₄ = –3.

Решение. Сначала система приводится к виду трапеции.

1-й шаг. Из 3-го уравнения вычитаеют 1-е уравнение, остальные уравнения сохраняют:

х₁ – 2х₂ + 3х₃ – 4х₄ = 4,

х₂ – х₃ + х₄ = –3,

5х₂ – 3х₃ + х₄ = –3,

–7х₂ + 3х₃ + х₄ = –3.

2-й шаг. 2-е уравнение умножают на 5 и прибавляют к 3-му уравнению, затем 2-е уравнение умножают на 7 и прибавляют к 4-му уравнению:

х₁ – 2х₂ + 3х₃ – 4х₄ = 4,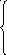

х₂ – х₃ + х₄ = –3,

2х₃ – 4х₄ = 12,

–4х₃ + 8х₄ = –24.

3-й шаг. 3-е уравнение умножают на 2 и прибавляют к 4-му уравнению:

х₁ – 2х₂ + 3х₃ – 4х₄ = 4,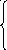

х₂ – х₃ + х₄ = –3,

2х₃ – 4х₄ = 12,

0 = 0.

4-й шаг. Нулевое равенство отбрасывают, получают систему, в которой три уравнения и четыре неизвестных. Такая система имеет бесконечное множество решений. Тогда х₄ объявляют свободной неизвестной, х₁, х₂, х₃ – зависимыми неизвестные. Последние выражают через х₄, для этого все слагаемы, содержащие х₄ , переносят вправо с противоположными знаками. Потом из полученного 3-го уравнения (2х₃ = 12 + 4х₄) находят выражение для х₃: х₃ = 6 + 2х₄. Это выражение подставляют во 2-е уравнение: х₂ = –3 + х₃ – х₄ и находят выражение для х₂: х₂ = 3 + х₄. Полученные выражения подставляют в 1-е уравнение (х₁ = 4 + 2х₂ – 3х₃ + 4х₄ ) и находят выражение для х₁: х₁ = – 8. Получают систему:

х₁ = – 8,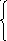

х₂ = 3 + х₄,

х₃ = 6 + 2х₄.

Это параметрическая запись общего решения исходной системы, в ней х₄ принимает произвольные числовые значения. И для каждого такого набора значений значения зависимых неизвестных х₁, х₂, х₃ вычисляют по предыдущим формулам, в результате будут получены все возможные решения системы.

Например, пусть х₄ = 0, тогда х₁ = – 8, х₂ = 3 + 0 =3, х₃ = 6 + 20 = 6, т.е. набор D₀ = (–8, 3, 6, 0) есть частное решение исходной системы. Пусть х₄ = 1, тогда х₁ = – 8, х₂ = 3 + 1 =4, х₃ = 6 + 21 = 8, т.е. набор D₁ = (–8, 4, 8, 1) – тоже частное решение исходной системы.

5-й шаг. Строят фундаментальную систему решений однородной системы:

х₁ – 2х₂ + 3х₃ – 4х₄ = 0,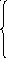

х₂ – х₃ + х₄ = 0,

х₁ + 3х₂ – 3х₄ = 0,

–7х₂ + 3х₃ + х₄ = 0.

Для этого повторяют преобразования, описанные на 14-х шагах, в результате х₄ окажется свободной неизвестной, и формулы для зависимых неизвестных примут вид:

х₁ = 0,

х₂ = х₄,

х₃ = 2х₄.

Так как свободная неизвестная одна, то и фундаментальная система решений однородной системы состоит из одного решения, которое получается по предыдущим формулам при х₄ = 1: С₁ = (0, 1, 2, 1) – базисное решение.

Теперь, формула (14) принимает вид: D = D₀ + m₁С₁. В качестве D₀ можно взять решение (–8, 3, 6, 0), полученное на 4-м шаге; m₁ принимает любые числовые значения. Тогда общее решение исходной неоднородной системы имеет вид:

(х₁, х₂, х₃, х₄) = (–8, 3, 6, 0) + m₁ (0, 1, 2, 1).

Например, решение D₁, найденное на 4-м шаге, получают при m₁ = 1:

D₁ = (–8, 3, 6, 0) + 1 (0, 1, 2, 1) = (–8, 4, 8, 1).