
- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
§1. Евклидово n-мерное пространство
Множество
всевозможных упорядоченных n–ок
вещественных чисел (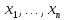 )
называетсяn-мерным
арифметическим пространством.
Такие
n–ки
чисел называются точками
этого пространства и обозначаются
M(
)
называетсяn-мерным
арифметическим пространством.
Такие
n–ки
чисел называются точками
этого пространства и обозначаются
M(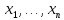 ).
Составляющие их числа называютсякоординатами
точек.
).
Составляющие их числа называютсякоординатами
точек.
Определение
1.
Евклидовым n-мерным
пространством
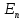 ,
называется
арифметическое пространство, в котором
расстояние между двумя точками
,
называется
арифметическое пространство, в котором
расстояние между двумя точками
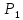 (
(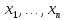 )
и
)
и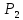 (
(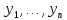 )
определяется по формуле:
)
определяется по формуле:
d(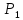 ,
,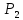 )
=
)
=
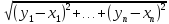
. (1)
Множество
точек
P
пространства
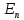 ,
удовлетворяющих условию
d(
,
удовлетворяющих условию
d(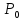 ,
,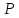 )
< ,
где
- положительное число, называется
-окрестностью
точки
)
< ,
где
- положительное число, называется
-окрестностью
точки
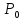 ,
, Пусть A
- множество точек пространства
Пусть A
- множество точек пространства
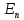 ,
Точка
,
Точка
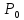 называетсявнутренней
точкой множества
A,
если она принадлежит A
вместе с некоторой –окрестность
этой точки. Множество A
называется открытым,
если все его точки внутренние.
называетсявнутренней
точкой множества
A,
если она принадлежит A
вместе с некоторой –окрестность
этой точки. Множество A
называется открытым,
если все его точки внутренние.
Множество
A
называется связным,
если любые две точки этого множества
можно соединить ломанной линией,
состоящей из точек этого множества
Областью
пространства
 называется открытое связное множествоA
точек
этого
пространства.
называется открытое связное множествоA
точек
этого
пространства.
Точка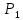 пространства
пространства
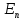 называется
граничной
точкой области
A,
если в любой –окрестности
точки
называется
граничной
точкой области
A,
если в любой –окрестности
точки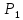 имеются точки пространства
имеются точки пространства
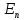 ,
как
принадлежащие A,
так и не принедлежащие A.
Совокупность всех граничных точек
области A
называется границей
области
A.
Область A
вместе со своей границей называется
замкнутой
областью,
она обозначается
,
как
принадлежащие A,
так и не принедлежащие A.
Совокупность всех граничных точек
области A
называется границей
области
A.
Область A
вместе со своей границей называется
замкнутой
областью,
она обозначается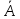 .
.
Определение 2. Точкой сгущения или предельной точкой множества A называется точка P, в любой окрестности которой имеются точки, отличные от P и принадлежащие A. Каждая предельная точка множества A является либо внутренней точкой A, либо - её граничной точкой.
В этом разделе подробно рассматривается понятие функции двух независимых переменных. Однако все введенные понятия и полученные результаты могут быть соответственно обобщены на случай функций любого числа независимых переменных.
Пусть A есть область изменения независимых переменных x и y.
Определение 3. Переменная z называется функцией от переменных x и y на множестве A, если каждой паре чисел (x,y) из А соответствует определенное значение z,. Переменные x и y назаваются также аргументами функции z. Множество А пар чисел, на которых определены значения функции z называется областью определения z.
Например,
областью определения функции z
= ln(1
–
x2
–
y2)
является открытое плоское множество
– внутренность круга, а для функции z
=
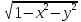 областью
определения
является замкнутое плоское множество
– внутренность круга, включая его
границу.
Для обозначения функции используется
запись z
=
f(x,y).
Переменные x,
y
можно заменить обозначением точки P
и писать z
=
f(P).
Особенно это удобно, когда рассматриваются
функции большого числа переменных.
областью
определения
является замкнутое плоское множество
– внутренность круга, включая его
границу.
Для обозначения функции используется
запись z
=
f(x,y).
Переменные x,
y
можно заменить обозначением точки P
и писать z
=
f(P).
Особенно это удобно, когда рассматриваются
функции большого числа переменных.
Графиком
функции
z
=
f(x,y
) называется множество точек
 ,
удовлетворяющих равенству:
z
=
f(x,y).
Геометрически в трехмерном пространстве
– это поверхность. Например, функции
,
удовлетворяющих равенству:
z
=
f(x,y).
Геометрически в трехмерном пространстве
– это поверхность. Например, функции
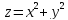 соответствует поверхность параболоида
вращения.
соответствует поверхность параболоида
вращения.
Определение 4. Линией уровня функции z = f(x,y) называется множество точек М(х, у), в которых эта функция принимает постоянное значение. Такое множество является некоторой линией на плоскости, и ее уравнение имеет вид: f(x,y) = С, где С – некоторое число.
Пример 1.a). Даноf(x,y)
=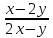 , вычислить:f(3,1) иf(1,2).
, вычислить:f(3,1) иf(1,2).
Решение. f(3,1) =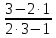 = 0,2;f(1,2) =
= 0,2;f(1,2) =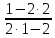 неопределено.
неопределено.
b), Даноz= 4 -x2 -y2. Областью определения является вся плоскоть, и областью изменения - полусегмент (-; 4];
c). Даноz=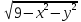 . Областью определения является
круг
. Областью определения является
круг
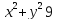 ,
и областью изменения - сегмент [0; 3];
,
и областью изменения - сегмент [0; 3];
Примеры 2. Построить линии уровня: а) для z = x2 – y, z = 0, 1;
b) для z = x2 - y2, z = 0, 1.
Решение: а) x2 – y = 0 – парабола; x2 – y =1- парабола;
b) x2 - y2 = 0 – две пересекающиеся прямые: y = x;
x2 - y2 =1 – гипербола.
Аналогично
определяется функция трех переменных
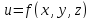 и соответствующие понятия.
и соответствующие понятия.
Пусть функция z = f(x,y) определена в плоской области А и М0 - точка сгущения множества А. Между точками на плоскости (и в евклидовом пространстве) определены расстояния: |M1M2| . Считается, что точка M стремится к точке M0, (обозначение: M M0 ), если расстояние между этими точками стремится к 0, (в таких случаях говорят также, что |M0M| есть бесконечно малая величина или |M0M| 0).
Определение 5. Число b называется пределом функции z = f(M) при
М
М0,
если разность | f(M)
- b|
есть бесконечно малая, когда М
М0.
Обозначение:
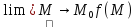 = b.
= b.
В этом определении подразумевается, что точка М может стремиться к точке М0 различными способами (например, по прямой линии или по некоторой кривой линии).
Определение 6. Функция z = f(M) называется непрерывной в точке М0, если f(M) определена в некоторой окрестпости М0 и выполняется
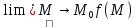 =
f(M0).
=
f(M0).
Функция
z
=
f(x,y)
называется
непрерывной
в области
А,
если она непрерывна в каждой точке этой
области. Функция
z
= f(x,y)
называется
непрерывной
в замкнутой области
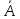 ,
если она непрерывна в каждой точке этой
области, а в точках границы этой области
имеет место непрерывность при условии,
что точка М
стремится к М0,
оставаясь внутри области А.
,
если она непрерывна в каждой точке этой
области, а в точках границы этой области
имеет место непрерывность при условии,
что точка М
стремится к М0,
оставаясь внутри области А.
Определение
7.
Величина
 называетсяприращение
аргумента x
в точке
называетсяприращение
аргумента x
в точке
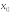 .
Величина
.
Величина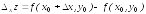 называется
частным
приращением
по
называется
частным
приращением
по
 функцииz
= f(x,y)
в
точке (
функцииz
= f(x,y)
в
точке (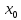 ,
,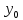 ).
).
Величина
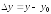 называется
приращение
аргумента
называется
приращение
аргумента
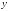 в точке
в точке .
Величина
.
Величина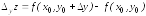 называется частным
приращением по
называется частным
приращением по
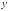 функцииz
=
f(x,y)
в
точке
(
функцииz
=
f(x,y)
в
точке
(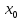 ,
,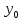 ).
).
Определение
8.
Частной
производной от функции
z
= f(x,y)
по
переменной x
в
(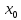 ,
,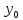 )
называется предел отношения
)
называется предел отношения
 к
к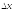 ,
когда
,
когда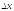 стремится к 0, если этот предел существует:
стремится к 0, если этот предел существует:
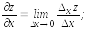
обозначения:
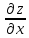 (
(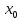 ,
,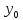 ),
),
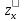 ,
,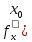 ,
,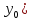 .
.
Частной
производной от функции
z
= f(x,y)
по
переменной
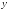 в точке(
в точке(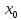 ,
,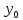 )
называется предел отношения
)
называется предел отношения
 к
к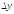 ,
когда
,
когда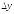 стремится к 0, если этот предел существует.
стремится к 0, если этот предел существует.
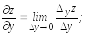
обозначения:
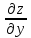 (
(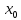 ,
,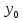 ),
),
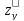 ,
,
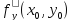 .
.
Пример 3. Вычислить частные производные функции z =x2y-3y2+5x.
Решение:
a)
при вычислении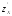 вычисляют обычную производную поx,
считая
y
постоянной величиной, получается:
вычисляют обычную производную поx,
считая
y
постоянной величиной, получается:
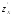 =
=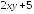 .
.
b)
при вычислении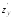 вычисляют обычную производная поy,
считая x
постоянной величиной, получается:
вычисляют обычную производная поy,
считая x
постоянной величиной, получается:
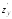 =
=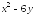 .
.
Пример
4.
Вычислить частные производные функции
z
=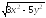
Решение:
a)
при вычислении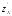 вычисляют обычную производную поx,
считая
y
постоянной величиной, получается::
вычисляют обычную производную поx,
считая
y
постоянной величиной, получается::
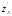 =
=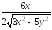 =
=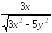 ;
;
b)
при вычислении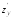 вычисляют обычную производная поy,
считая x
постоянной величиной, получается:
вычисляют обычную производная поy,
считая x
постоянной величиной, получается:
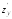 =
=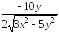 =
=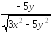 .
.
Рассматривается
функция двух переменных z
= f(x,y)
и
приращения аргументов:
 и
и
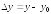 .Полным
приращением
называется разность: z
= f(x0+x,
y0
+y)
- f(x0,y0).
Функция z
= f(x,y)
называется
дифференцируемой
в
точке
.Полным
приращением
называется разность: z
= f(x0+x,
y0
+y)
- f(x0,y0).
Функция z
= f(x,y)
называется
дифференцируемой
в
точке
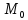 (
( ,
,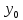 ),
если в этой точке полное приращение
можно представить в следующем виде z
=
),
если в этой точке полное приращение
можно представить в следующем виде z
=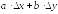 +
+
 ,
гдеa,
b
-
числа и
,
гдеa,
b
-
числа и
 обозначает бесконечно малую величину
при
0,
где
=
обозначает бесконечно малую величину
при
0,
где
=
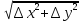 .
При этом величина [
.
При этом величина [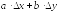 ]
называетсялинейной
частью
полного приращения
]
называетсялинейной
частью
полного приращения
 относительно
относительно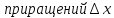 и
и
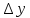 .
.
.
Определение
9.
Полным
дифференциалом
функции z
= f(x,y)
в
точке
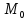 (
(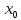 ,
,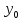 )
называется линейная часть полного
приращения
)
называется линейная часть полного
приращения
 относительно приращений
относительно приращений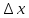 ,
,
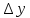 .
Обозначение:
.
Обозначение:
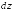 ,
,
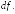
Доказывается,
что если функция
z
= f(x,y)
имеет непрерывные частные производные,
то ее полный дифференциал вычисляется
по формуле: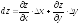 ,
где частные производные вычисляются
в заданной точке. В частности, дифференциалы
переменных
,
где частные производные вычисляются
в заданной точке. В частности, дифференциалы
переменных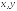 совпадают со своими приращениями:
совпадают со своими приращениями: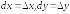 .
Поэтому
.
Поэтому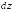 записывают в виде:
записывают в виде:
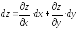
При
достаточно малом
=
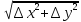 справедливо
приближенное равенство
справедливо
приближенное равенство
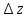
dz.
Из этого равенства получается следующая
формула, используемая для приближенного
вычисления значения функции:
dz.
Из этого равенства получается следующая
формула, используемая для приближенного
вычисления значения функции:
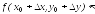
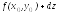
.
Пример
5. Найти
полный дифференциал функции z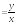
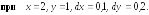
Решение. Вычисляют частные производные в точке (2;1):
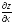 =
=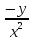 =
=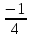 ;
;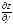 =
= ;
тогда
;
тогда
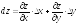 =
=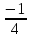 ∙0,1+
∙0,1+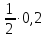 = 0,075.
= 0,075.
Пример
6. При
деформации цилиндра, его радиус R
увеличился с 2 до 2,05 дм. , а высота
уменьшилась с 10 до 9,8 дм. Найти приближенное
изменение объема цилиндра V
по формуле
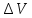
dV.
dV.
Решение.
Объем цилиндра равен V
=
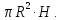 По
условию
По
условию
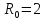 ;
;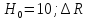 = 0,05;
= 0,05;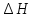 = - 0,2.
= - 0,2.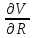 =
2RH
=
40;
=
2RH
=
40;
 =
=
 =
4.
=
4.
Тогда
dV
=
40∙0,05+4∙(-0,2)
= 1,2
3,768 дм3.
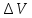 3,768
дм3
3,768
дм3
Определение
10.
Частными
производными
второго порядка
от функции z
= f(x,y)
называются
частные производные от ее частных
производных первого порядка. При этом
возникают частные
производные второго порядка отдельно
по
х
( и
отдельно по
y
и
отдельно по
y
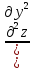 ;
а
также две смешанные производные:
;
а
также две смешанные производные:
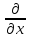 (
(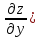 =
=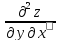
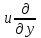 (
(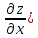 =
=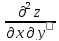 .
.
Теорема
1.
Если
смешанные производные непрерывны в
рассматриваемой точке, то они равны
между собой:
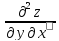 =
=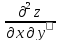 .
.
Пример
7. Пусть
z = y∙ln
x..
Вычисляют,частные производные первого
порядка:
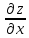 =
=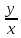 и
и
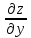 = ln x.
Теперь производят повторное
дифференцирование:
= ln x.
Теперь производят повторное
дифференцирование:
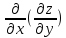 =
=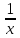 ;
;
 =
=
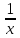 .
Получились равные функции, что и
утверждается в теореме 1.
.
Получились равные функции, что и
утверждается в теореме 1.
Определение 11. Дифференциалом второго порядка от функции z = f(x,y) называется дифференциал от ее полного дифференциала, то есть
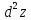 =
d(dz).
=
d(dz).
Теорема
2.
Если x и
y
–
независимые переменные и функция f(x,y)
имеет
непрерывные частные производные второго
порядка, то дифференциал второго порядка
вычисляется по формуле
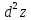 =
=
 + 2
+ 2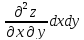 +
+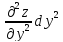 .
.
.
