
- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
§2. Дифференциальные уравнения 2-го порядка
Дано дифференциальное уравнение 2–го порядка
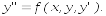
(5)
.
Начальные
условия
– это три числа
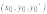 ,
Функцияy=g(x)
удовлетворяет
начальным усдовиям
,
Функцияy=g(x)
удовлетворяет
начальным усдовиям
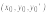 ,
если выполняются равенства:
,
если выполняются равенства:
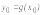 и
и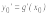 .
.
Задача
Коши.
Для данных начальных условий
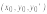 найти
решение дифференциального уравнения,
удовлетворяющее
этим условиям.
найти
решение дифференциального уравнения,
удовлетворяющее
этим условиям.
Теорема существования решения задачи Коши
Пусть
В
– трехмерная область , в которой правая
часть
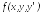 и ее частные производные
и ее частные производные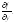
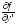 по
переменным
по
переменным
y
,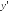 непрерывны.
Тогда для любой точки
непрерывны.
Тогда для любой точки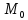
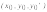 изВ
существует и притом единственное
решение
изВ
существует и притом единственное
решение
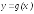 уравнения (5), удовлетворяющее начальным
условиям
уравнения (5), удовлетворяющее начальным
условиям .
.
Определение
5.
Общим решением
дифференциального уравнения
2-го порядка
называется функция y
= (x,
 ).
вида (2), содержащая две константу
).
вида (2), содержащая две константу
 ,
, которая при любых значениях
которая при любых значениях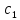 ,
,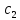 является решением данного уравнения и
для любой точки
является решением данного уравнения и
для любой точки
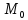
 из
указанного множества В
найдется
значение константы
из
указанного множества В
найдется
значение константы
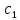 ,
,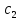 при которых она удовлетворяет начальным
условиям
при которых она удовлетворяет начальным
условиям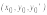 .
.
Методы понижения порядка.
1-й
тип.
Пусть дифференциальное уравнение имеет
вид
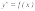 ,
т.е. правая часть не содержитy
и
,
т.е. правая часть не содержитy
и
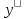 . Такое уравнение решается двойным
интегрированием: сначала находят
. Такое уравнение решается двойным
интегрированием: сначала находят ,
затем
,
затем
Пример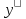 =
cosx.
=
cosx.
Решение.
. Интегрируют последовательно два раза:
1).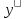 =
=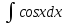 =sinx
+
=sinx
+
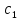 ;
2).y=
;
2).y=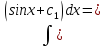 -
cosx+
-
cosx+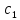 +
+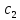 .
.
2-й
тип.
Пусть дифференциальное уравнение имеет
вид
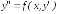 ,
т.е правая часть явно не содержитy.
Такое уравнение решается заменой
,
т.е правая часть явно не содержитy.
Такое уравнение решается заменой
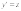 .
Получается уравнение 1-го порядка
относительно z:
.
Получается уравнение 1-го порядка
относительно z: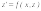 .
Из него находят
.
Из него находят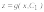 ,
затем находяту:
,
затем находяту:
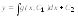 .
.
3-й
тип.
Пусть дифференциальное уравнение имеет
вид
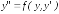 ,
т.е. правая часть явно не содержитx.
решается заменой
,
т.е. правая часть явно не содержитx.
решается заменой
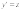 и
и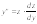 Получается дифференциальное уравнение
1-го порядка:
Получается дифференциальное уравнение
1-го порядка:
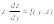 относительно
z
и y
. Из него находят
относительно
z
и y
. Из него находят
 ,
затем находяту
из дифференциально уравнения
,
затем находяту
из дифференциально уравнения

Пример
5. Найти
общее решение
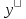 =y.
=y.
Решение.
Это ДУ 2-го порядка. Для его интегрирования
нужно понизить порядок уравнения. Делают
замену:
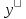 =z.
При этом считают, что z
является функцией от y.
Тогда
=z.
При этом считают, что z
является функцией от y.
Тогда
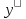 =
=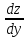 ∙
∙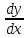 =z∙
=z∙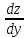 .
Это подставляют в исходное уравнение:z∙
.
Это подставляют в исходное уравнение:z∙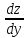 =y
– это уравнение 1-го порядка с
разделяющимися переменными. Разделяют
переменные. zdz=ydy,
интегрируют:
=y
– это уравнение 1-го порядка с
разделяющимися переменными. Разделяют
переменные. zdz=ydy,
интегрируют: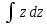 =
=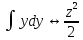 =
=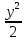 +
+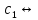 z=
z=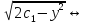
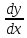 =
=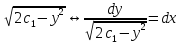
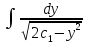 =
=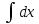 +
+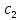 arcsin
arcsin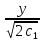 =
x+
=
x+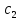
В следующих разделах вводятся основные понятия, связанные с линейными дифференциальными уравнениями. Для простоты изложения рассматриваются только уравнения 2-го порядка, но эти понятия легко переносятся на уравнения более высоких порядков.
§3. Линейные уравнения 2-го порядка
Общий вид линейных уравнений 2-го порядка:
у''+p(x)y'+q(x)y = f(x), (1)
где
p(x),
q(x),
f(x)
– функции от х
.Согласно
условиям существования решения задачи
Коши для таких уравнений, принято
считать, что функции
p(x),
q(x)
,
f(x)
непрерывны
в некотором интервале (a;
b).
Тогда это уравнение имеет общее решение
у
=
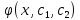 .
Если f(x)=
0, то (1) называется однородным.
Но сначала рассматривается несколько
важных утверждений об однородных
уравнениях, поэтому их вид размещен
отдельно.
.
Если f(x)=
0, то (1) называется однородным.
Но сначала рассматривается несколько
важных утверждений об однородных
уравнениях, поэтому их вид размещен
отдельно.
у''+p(x)y'+q(x)y =0, (2)
Теорема
1.
Если
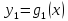 ,
,
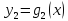 решения уравнения (2), то любая линейная
комбинация этих функций является
решением (2).
решения уравнения (2), то любая линейная
комбинация этих функций является
решением (2).
Доказательство.
Пусть выполняется условие теоремы,
тогда выполняются следующие тождества:
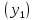 ''+p(x)
''+p(x)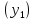 '+q(x)(
'+q(x)(
0,
0,
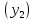 ''+p(x)
''+p(x)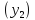 '+q(x)(
'+q(x)(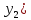
0.
0.
Отсюда,
согласно свойствам производных, легко
следует, то линейная комбинация
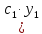 +
+
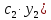 удовлетворяет этому уравнению. Теорема
доказана.
удовлетворяет этому уравнению. Теорема
доказана.
Определение
5.
Функции
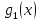 и
и
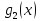 называются
линено
зависимыми на
интервале (a,
b),
если их отношение на этом интервале
равно постоянному числу:
называются
линено
зависимыми на
интервале (a,
b),
если их отношение на этом интервале
равно постоянному числу:
 .
В противном случае эти функции называются
линейно
независимыми
на
(a,
b).
.
В противном случае эти функции называются
линейно
независимыми
на
(a,
b).
Например,
(sin
kx
и cos
mx)
или
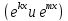 пары линено независимых функций, если
k
m.
пары линено независимых функций, если
k
m.
Для
описания некоторых свойств уравнений
(1) вводится следующий определитель,
называется определителем
Вронского
для функций
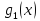 и
и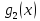 ,
и обозначается указанным способом.
,
и обозначается указанным способом.
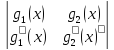 =
W(
=
W(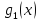 ,
,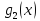 ).
).
Теорема
2. Если
функции
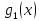 и
и
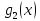 линейно
зависимые на интервале
(a,
b),
то соответствующий им определитель
Вронского равен 0 на этом интервале.
линейно
зависимые на интервале
(a,
b),
то соответствующий им определитель
Вронского равен 0 на этом интервале.
Доказательство.
Пусть
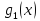 и
и
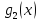 удовлетворяют условию,
удовлетворяют условию,
тогда
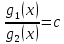 на
(a,
b).
Следовательно, W(
на
(a,
b).
Следовательно, W(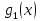 ,
,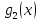 )
=
)
=
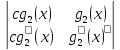 = 0, теорема доказана.
= 0, теорема доказана.
Теорема
3 (Лиувиля).
Пусть функции
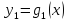 ,
,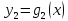 являются решениями линейного однородного
дифференциального уравнения (2) .
ОпределительW(
являются решениями линейного однородного
дифференциального уравнения (2) .
ОпределительW(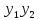 )
для этих функций либо отличен от 0 во
всех точках интервала (a,
b).
либо он равен 0 во всех точках этого
интервала.
)
для этих функций либо отличен от 0 во
всех точках интервала (a,
b).
либо он равен 0 во всех точках этого
интервала.
Доказательство.
Пусть
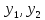 удовлетворяют условию теоремы.Непосредственной
подстановкой проверяется, что
W(
удовлетворяют условию теоремы.Непосредственной
подстановкой проверяется, что
W(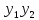 )
является решением следующего уравнения
)
является решением следующего уравнения
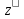 -p∙z
= 0. Cледовательно, W(
-p∙z
= 0. Cледовательно, W(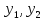 )
= С∙
)
= С∙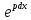 .
Тогда при С
= 0 W(
.
Тогда при С
= 0 W(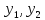 )=
0 во всех точках интервала
(a,
b).
А если С
0, то W(
)=
0 во всех точках интервала
(a,
b).
А если С
0, то W(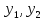 )
отличен от 0 во всех точках интервала
(a,
b).Теорема
доказана.
)
отличен от 0 во всех точках интервала
(a,
b).Теорема
доказана.
Далее, доказываеся следующее утверждение.
Теорема
4.
Пусть
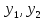 удовлетворяют условию предыдущей
теоремы. Тогда равенствоW(
удовлетворяют условию предыдущей
теоремы. Тогда равенствоW(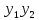 )=0
является необходимым и достаточным
условием линейной зависимости этих
решений
)=0
является необходимым и достаточным
условием линейной зависимости этих
решений
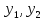 .
.
Доказательство этой теоремы не сложное, но оно использует большое количество мелких вспомогательных утверждений, и потому здесь не приводится. С помощью этой теоремы доказывают следующие важные следствия.
Следствие 1. Общее решение линейного однородного уравнения (2) имеет вид
 ,
,
где
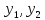 линейно независимые решения этого
уравнения, и
линейно независимые решения этого
уравнения, и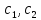 – произвольные постоянные.
– произвольные постоянные.
Следствие
2.
Пусть (1)
- неоднородное уравнение и (2) получается
из (1) заменой f(x)
на 0, тогда общее
решение уравнения (1) имеет вид
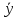 +
+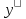 ,
,
где
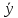 - общее решение (2) и
- общее решение (2) и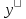 -
частное решение (1).
-
частное решение (1).
Далее, методы решения линейных уравнений рассматривают на примере уравнений вида (1), когда его коэффициенты являются постоянными числами. Для этого сначала описывают специальный метод построения линено независимых решений однородных уравнений с постоянными коэффициентами. Пусть дано уравнение вида (2) с постоянными коэффициентами:
у''+py'+qy =0, (3)
Решение ищут в виде: у=екх, где k – параметр. Тогда
у' = kekx, у'' = k2ekx . При подстановке в (3), получают равенство:
(к2+ pк +q) екх= 0. В этом равенстве екх 0, поэтому к2+pк+q=0. Это так называемое, характеристическое уравнение. С помощью его корней строят решения исходного (3).
Случай
1.
Пусть D=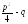 >0,
тогда корник1
и
к2
- вещественные и различные: к1,2
= -p/2
>0,
тогда корник1
и
к2
- вещественные и различные: к1,2
= -p/2
 .
Следовательно,
.
Следовательно,
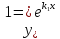 ,
,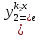 являются линейно независимыми решениями
(3) и, по следствию 1,общее
решение
имеет вид:
являются линейно независимыми решениями
(3) и, по следствию 1,общее
решение
имеет вид:
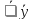 =
=
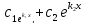 .
.
Случай
2.
Пусть D=
0, тогда корни равные: к1
= к2
=
- p/2.
В этом случае полагают:
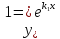 ,
,
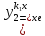 и
и
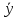 =
=
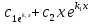 -
общее решение (1).
-
общее решение (1).
Случай
3.
Пусть D < 0, тогда корни комплексные:
к1,2
=i.
В этом случае полагают у1=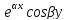 и у2=
и у2=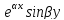 и
и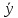 =
=
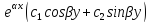 .
.
Пример 6. Решить уравнение у''-5у'+6у=0.
Решение. Составляют характеристическое уравнение: к2-5к+6=0.
Находят
его корни: к1=2,
к2=3.
Тогда
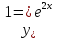 ,
,
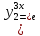 являются линейно независимыми решениями
иобщее
решение
имеет вид:
являются линейно независимыми решениями
иобщее
решение
имеет вид:
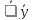 =
=
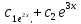 .
.
Пример 7. Решить уравнение у''- 12у' + 144у = 0.
Решение:
Составляют характеристическое уравнение:
к2-12к+144=0.
к1=к2=12.
Следовательно, ,
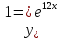 ,
,
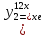 и
и
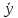 =
=
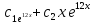 -
общее решение.
-
общее решение.
Пример 8. Решить уравнение у'' - 6у' + 25у=0.
Решение: Составляют характеристическое уравнение: к2 - 6к + 25 = 0. Находят D = - 16 < 0, корни комплексные: k1,2 = = 3 4i. Тогда
Общее
решение:
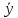 =
е
3х(С1cos4x
+C2sin4x).
=
е
3х(С1cos4x
+C2sin4x).
