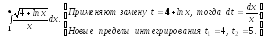- •В.А.Ганов учебно-методический комплекс
- •280700.62 «Техносферная безопасность»
- •Оглавление
- •Пояснительная записка
- •1). Цели и задачи дисциплины, ее место в учебном процессе
- •2). Общие пояснения
- •2.Основные требования государственного образовательного стандарта
- •3.2. Содержание учебной дисциплины
- •4. Разделы учебной дисциплины, виды учебной деятельности и формы контроля
- •5. Самостоятельная работа студента
- •5.1. График самостоятельной работы студента
- •6. Оценочные средства для контроля успеваемости ирезультатов освоения учебной дисциплины
- •7.Литература
- •2.5.1. Основная литература
- •7. Материально-техническое обеспечение учебной дисциплины
- •2.6.1. Требования к аудиториям (помещениям, местам) для проведения занятий:
- •7.2. Требования к оборудованию рабочих мест преподавателя и обучающихся:
- •8.Тематический план (распределение часов курса по темам и видам работ):
- •1 Семестр
- •2 Семестр
- •3 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •1 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •2 Семестр
- •7. Учебно-методическая (технологическая) карта дисциплины.
- •3 Семестр
- •10.Контрольные задания и тесты
- •Вариант 2.
- •13.Какой из следующих определителей не равен нулю?
- •Вариант 2
- •Вариант 19
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 27
- •Утверждаю: Зав. Кафедрой_________________
- •11.1. Вопросы к экзамену по дисциплине «Высшая математика»,
- •8.1.2.Экзаменационные билеты по высшей математике
- •11.2.Экзаменационные вопросы
- •11.2.Экзаменационные билеты (2-й семестр)
- •8.3.1.Экзаменационные вопросы
- •8.3.2.Экзаменационные билеты по высшей математике 3-й семестр
- •Учебные пособия
- •Оглавление
- •Глава 1. Элементы линейной алгебры
- •§1. Числовые матрицы и определители
- •Основные свойства матриц
- •Основные свойства определителей
- •§2. Обратная матрица
- •§3. Системы линейных уравнений
- •2) Если определитель а равен нулю и хотя бы один из I отличен от нуля, то система (5) не имеет решений;
- •3) Если определитель а и все вспомогательные определители I равны нулю, то система (5) имеет бесконечное множество решений.
- •1) Если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;
- •2) Если (7) содержит противоречие, то система (3) не имеет решений;
- •3) Если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.
- •§4. Ранг матрицы и неопределенные системы
- •Упражнения 1
- •Глава 2. Аналитическая геометрия
- •§1. Декартова система координат
- •§2. Уравнение прямой линии на плоскости
- •§3. Кривые линий второго порядка
- •§4. Декартовы координаты и векторы в пространстве
- •2). Координаты точки деления отрезка в заданном отношении вычисляют по формулам:
- •§5. Скалярное произведение векторов
- •Свойства скалярного произведения
- •§6. Векторное и смешанное произведения
- •Свойства векторного произведения
- •§7. Плоскость и прямая линия в пространстве
- •2).Условие параллельности плоскостей:
- •Основное правило 1.
- •2).Условие параллельности прямых:
- •Основное правило 2.
- •Упражнения 2
- •Глава 3. Поверхности второго порядка
- •§1.Сферические, цилиндрические и конические поверхности
- •Частные случаи.
- •§2.Стандартные поверхности 2-го порядка
- •§3. Поверхности вращения
- •Упражнения 3
- •Глава 4. Комплексные числа
- •§1. Алгебраическая форма комплексного числа
- •§2. Тригонометрическая форма комплексного числа
- •Упражнения 4
- •Глава 5. Разложение рациональных дробей
- •Правило разложения правильной вещественной дроби на простейшие дроби.
- •Глава 6. Введение в математический анализ
- •§1. Числовые функции
- •§2. Простейшие функции
- •Основные свойства степеней
- •Основные свойства логарифмов
- •6. Тригонометрические функции.
- •Обратные тригонометрические функции.
- •§3. Бесконечные величины и предел функции
- •Свойства пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Теперь исходный предел равен: §4. Непрерывные функции
- •3) F(X) принимает на [a; b] все промежуточные значения между своими наименьшим и наибольшим значениями.
- •Упражнения 4
- •Упражнения 5
- •Библиографический список
- •Часть 2
- •Глава 1. Дифференциальное исчисление………………………………………………….5
- •§1. Производная функции одной переменной
- •Правила дифференцирования
- •§2. Задачи, приводящие к понятию производной функци
- •§4. Основные теоремы о дифференцируемых функциях
- •§5. Исследование функций на монотонность и экстремум
- •Задачи на экстремум.
- •§6. Вогнутость и точки перегиба
- •Определение 6.Точки, в которых график функции меняет направление вогнутости называютсяточками перегиба.
- •Упражнения 1
- •Ответы к упражнениям 1
- •Глава 2. Интегральное исчисление
- •§1. Неопределенный интеграл
- •Правила интегрирования
- •Основные свойства неопределенных интегралов
- •§2. Методы интегрирования
- •3.Интегрирования по частям. Пусть u и V - дифференцируемые функции от х, тогда верно равенство
- •5. Интегрирование некоторых тригонометрических функций.
- •§3. Определенный интеграл
- •Свойства определенного интеграла
- •§4.Приложения определенных интегралов
- •1.Вычисление площади плоской фигуры, ограниченной линиями
- •§5. Несобственные интегралы
- •Упражнения 2
- •Ответы к упражнениям 2
- •Глава 3. Функции нескольких переменных
- •§1. Евклидово n-мерное пространство
- •§2. Экстремумы функций двух переменных
- •§3. Метод наименьших квадратов
- •Упражнения 3
- •Глава 4. Функции комплексного переменного
- •§1. Определение и геометрическое и изображение
- •Предел и непрерывность функции комплексного переменного
- •§2. Элементарные функции комплексного переменного
- •§3. Дифференцирование
- •Другие свойства
- •Геометрический смысл производной
- •Глава 5. Дифференциальные уравнения
- •§1. Дифференциальные уравнения 1-го порядка
- •Теорема о существовании решения задачи Коши
- •Методы интегрирования дифференциальных уравнений
- •§2. Дифференциальные уравнения 2-го порядка
- •Теорема существования решения задачи Коши
- •Методы понижения порядка.
- •§3. Линейные уравнения 2-го порядка
- •§4. Линейные уравнения с постоянными коэффициентами
- •Упражнения 5
- •Глава 8.Элементы теории вероятностей
- •§1.Определение вероятности и ее свойства
- •Свойства вероятности
- •§2. Повторные независимые испытания
- •§3. Случайные величины
- •Основные свойства функции распределения f(X)
- •Основные свойства плотности распределения f(X)
- •Свойства математического ожидания
- •Свойства дисперсии
- •Основные виды распределений
- •§4. Закон больших чисел
- •Приложение 1.Элементы комбинаторики Основные правила комбинаторики
- •Простейшие соединения
- •Упражнения 7
- •Упражнение 8
- •Библиографический список
- •Приложение 2. Математико-статистические таблицы
- •Глава 8. Введение в математическую статистику
- •§1. Выборочный метод
- •Основные виды распределений
- •Упражнение 8
5. Интегрирование некоторых тригонометрических функций.
Интегралы
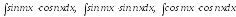
используют формулы преобразования произведения в сумму (см. часть 1 глава 5 §1).
Пример
9.
=
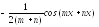 -
-
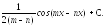
Интегралы
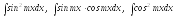 используют формулы понижения степени,
( часть 1 глава 5 §1).
используют формулы понижения степени,
( часть 1 глава 5 §1).
Пример
10.
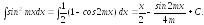
б).
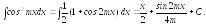
в).
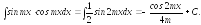
Интегралы
вида
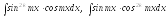 используют заменыsinmx
= t,
cosmx
= t,
соответственно.
используют заменыsinmx
= t,
cosmx
= t,
соответственно.
Пример
11.
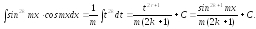
б).

§3. Определенный интеграл
Пусть функция f(x) определена на отрезке [a;b]. Этот отрезок разбивают наn частей (xi-1; xi),i = 1, …,n, точками:а =х0<x1<x2< … <xn =b, и пустьx1,x2, …,xn - длины отрезков разбиения. Из каждого такого отрезка выбирается произвольная точкаi, вычисляется значениеf(i), и составляется сумма
S1 =f(1)x1 +f(2)x2 + … + f(n)xn. (5)
Эта сумма называется интегральной суммой для f(x)на[a;b].
Затем, отрезки (xi-1; xi) разбивают на более мелкие части, из них выбираются новые точки и составляют новую интегральную суммуS2 вида (6). Этот процесс разбиения отрезка [a;b] и составление соответствующих интегральных сумм продолжается бесконечно. В результате возникает бесконечная последовательность интегральных сумм:S1, S2, S3, … .
Определение 3. Определенным интегралом от функции f(x) в пределах от а до b называется предел указанных выше интегральных сумм, когда отрезок [a;b] бесконечно измельчается, если этот предел существует и не зависит от способов разбиения и выбора точек.Обозначение:
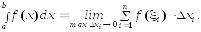
(6)
Числа a,bназываютсяпределами интегрирования.
Построение интегральной суммы иллюстрируется на рис.1.
yy
= f(x)f(n)
В
f
(2) 




f(1)


А…
x
0 a1x1
2
x2
. . . xn-1
n
b
Рис. 1.
Через точки деления а,x,
x2,
…,xn,
bпроведены отрезки,
параллельные оси ОY, и образованы прямоугольники с
основаниями и высотамиf(1),f(2),
…, f(n).
Тогда площади этих прямоугольников
равныf(1)x1,f(2)x2
, …, f(n)xn,
соответственно, и их суммаf(i)xiявляется приближенным значением площади
всей криволинейной трапецииаАВb.
и высотамиf(1),f(2),
…, f(n).
Тогда площади этих прямоугольников
равныf(1)x1,f(2)x2
, …, f(n)xn,
соответственно, и их суммаf(i)xiявляется приближенным значением площади
всей криволинейной трапецииаАВb.
Если производить более мелкие разбиения [a;b], то соответствующие суммыf(i)xi будут приближаться к истинному значению площади аАВb.Поэтомуплощадью криволинейной трапеции аАВb назван предел указанных суммf(i)xi, когда отрезок [a;b] бесконечно измельчается.
С другой стороны, эти суммы являются интегральными суммами для функции f(x)на[a;b]. Вывод:
определенный интеграл положительной функции y = f(x) по отрезку [a; b] равен площади криволинейной трапеции аAВb.
Свойства определенного интеграла
Здесь подразумевается, что интегралы, указанные в правых частях пунктов 2 - 5, существуют; и в пункте 7 неравенство функций рассматривается на [a;b].
Теорема 2.Пусть f(x)непрерывна на [a;b].Тогда она имеет первообразную F(x)на [a;b]и верна формула:
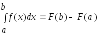
(7)
Эта формула называется формулой
Ньютона-Лейбница. Она означает,
что определенный интеграл от непрерывной
функции равен разности значений
первообразной функции при верхнем и
нижнем пределах интегрирования.Эта разность обозначается: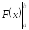
Примеры 9.Вычислить определенные
интегралы.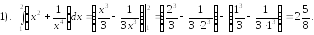
Важное место среди свойств занимает
следующее утверждение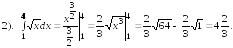
Теорема о среднем. Если функция f(x) непрерывна на [a; b], то между a и b найдется число с такое, что выполняется равенство:
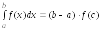
Величина f(c) называетсясредним значением функцииf(x)на[a;b].
Пример 10.Определить среднее значение функции у =х2 на[1; 3].
Решение.Здесьf(x) =x2 . Вычисляют интеграл:
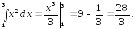
Теперь,
по теореме о среднем, получают: 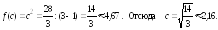
Вывод: среднее значение приближенно равно 4,67 прих2,16.
Из теоремы 2 следует, что для непрерывных функций методы интегрирования для неопределенного интеграла можно применять и для определенного интеграла со следующими дополнениями.
В методе интегрирования подстановкойформула (3) принимает вид:
(8)
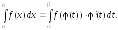
В методе интегрирования по частямформула (4) принимает вид:
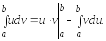
(9)
Примеры 11.Вычислить определенный
интегра